27.2.3 相似三角形应用举例(2) 课件(共14张PPT)
文档属性
| 名称 | 27.2.3 相似三角形应用举例(2) 课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 155.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-10 17:21:59 | ||
图片预览



文档简介
(共14张PPT)
第二十七章 相 似
27.2.3 相似三角形应用举例(2)
一、新课引入
利用相似可以解决生活中的问题,计量一些无法直接测量的物体的长度.解题的关键在于构建相似三角形.
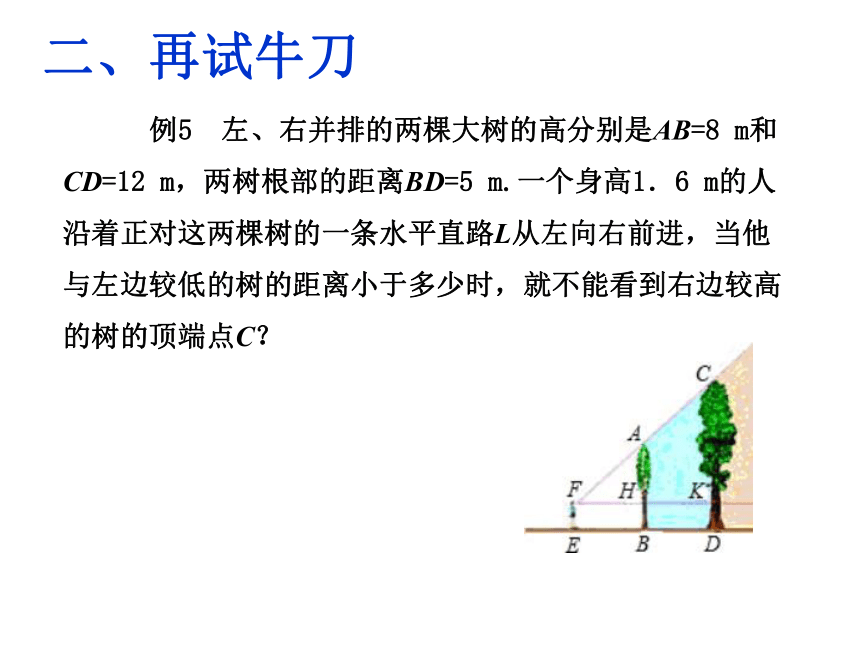
例5 左、右并排的两棵大树的高分别是AB=8 m和CD=12 m,两树根部的距离BD=5 m.一个身高1.6 m的人沿着正对这两棵树的一条水平直路L从左向右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C?
二、再试牛刀
你能设计方案,利用相似三角形的知识测量旗杆的高度吗?
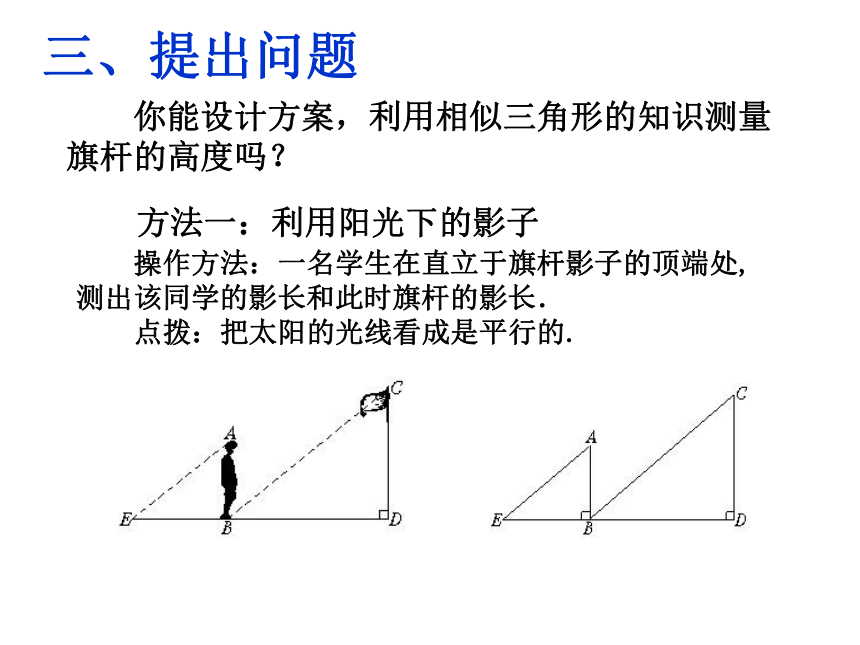
方法一:利用阳光下的影子
三、提出问题
操作方法:一名学生在直立于旗杆影子的顶端处,测出该同学的影长和此时旗杆的影长.
点拨:把太阳的光线看成是平行的.
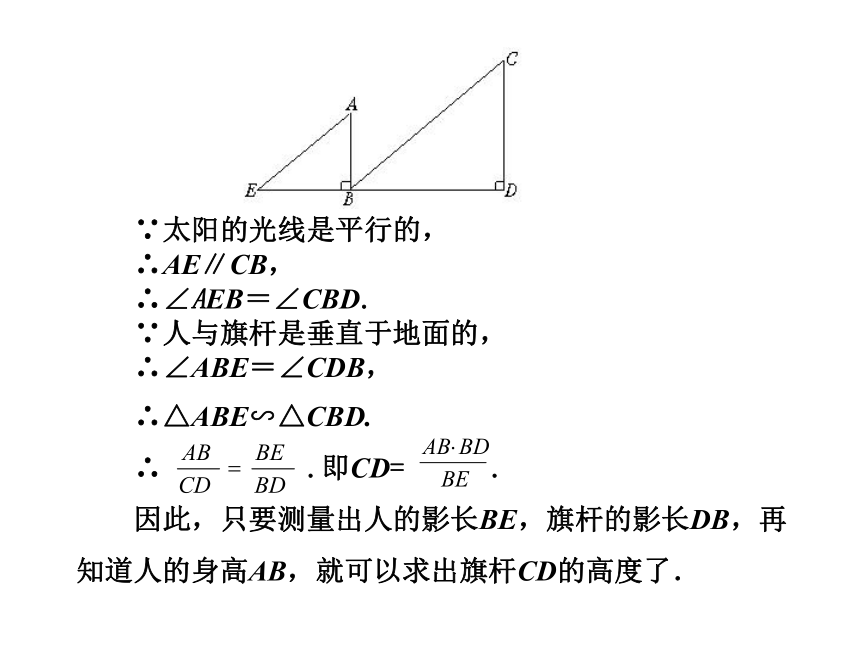
∵太阳的光线是平行的,
∴AE∥CB,
∴∠AEB=∠CBD.
∵人与旗杆是垂直于地面的,
∴∠ABE=∠CDB,
∴△ABE∽△CBD.
∴ .即CD= .
因此,只要测量出人的影长BE,旗杆的影长DB,再知道人的身高AB,就可以求出旗杆CD的高度了.
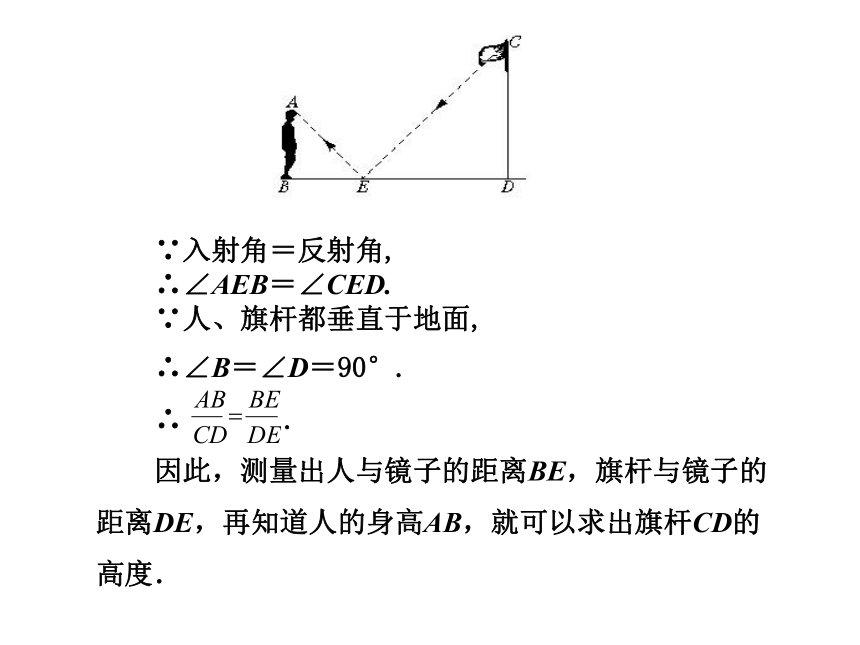
方法二:利用镜子的反射
操作方法:选一名学生作为观测者.在他与旗杆之间的地面上平放一面镜子,固定镜子的位置,观测者看着镜子来回调整自己的位置,使自己能够通过镜子看到旗杆项端.测出此时他的脚与镜子的距离、旗杆底部与镜子的距离就能求出旗杆的高度.
点拨:入射角=反射角
∵入射角=反射角,
∴∠AEB=∠CED.
∵人、旗杆都垂直于地面,
∴∠B=∠D=90°.
∴ .
因此,测量出人与镜子的距离BE,旗杆与镜子的距离DE,再知道人的身高AB,就可以求出旗杆CD的高度.
方法三:利用标杆测量旗杆的高度
操作方法:选一名学生为观测者,在他和旗杆之间的地面上直立一根高度已知的标杆,观测者前后调整自己的位置,使旗杆顶部、标杆顶部与眼睛恰好在同一直线上时,分别测出他的脚与旗杆底部,以及标杆底部的距离即可求出旗杆的高度.
点拨:人、标杆和旗杆都垂直于地面.
∵人、标杆和旗杆都垂直于地面,
∴∠ABF=∠EFD=∠CDH=90°,
∴人、标杆和旗杆是互相平行的.
∵EF∥CN,∴∠1=∠2.
∵∠3=∠3,△AME∽△ANC,
∴ .
∵人与标杆的距离、人与旗杆的距离,标杆与人的身高的差EM都已测量出,
∴能求出CN.
∵∠ABF=∠CDF=∠AND=90°,
∴四边形ABND为矩形.
∴DN=AB.
∴能求出旗杆CD的长度.
如图,测得BD=120 m,DC=60 m,EC=50 m,求河宽AB.
四、运用提高
100 m.
谈谈你在本节课的收获.
五、课堂小结
1.必做题:
教材第55,56页习题27.2第10、11题.
2.选做题:
教材第56页习题27.2第16题.
六、布置作业
3.备选题:
一盗窃犯于夜深人静之时潜入某单位作案,该单位的自动摄像系统摄下了他作案的全过程.请你为警方设计一个方案,估计该盗窃犯的大致身高.
再见!
第二十七章 相 似
27.2.3 相似三角形应用举例(2)
一、新课引入
利用相似可以解决生活中的问题,计量一些无法直接测量的物体的长度.解题的关键在于构建相似三角形.
例5 左、右并排的两棵大树的高分别是AB=8 m和CD=12 m,两树根部的距离BD=5 m.一个身高1.6 m的人沿着正对这两棵树的一条水平直路L从左向右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C?
二、再试牛刀
你能设计方案,利用相似三角形的知识测量旗杆的高度吗?
方法一:利用阳光下的影子
三、提出问题
操作方法:一名学生在直立于旗杆影子的顶端处,测出该同学的影长和此时旗杆的影长.
点拨:把太阳的光线看成是平行的.
∵太阳的光线是平行的,
∴AE∥CB,
∴∠AEB=∠CBD.
∵人与旗杆是垂直于地面的,
∴∠ABE=∠CDB,
∴△ABE∽△CBD.
∴ .即CD= .
因此,只要测量出人的影长BE,旗杆的影长DB,再知道人的身高AB,就可以求出旗杆CD的高度了.
方法二:利用镜子的反射
操作方法:选一名学生作为观测者.在他与旗杆之间的地面上平放一面镜子,固定镜子的位置,观测者看着镜子来回调整自己的位置,使自己能够通过镜子看到旗杆项端.测出此时他的脚与镜子的距离、旗杆底部与镜子的距离就能求出旗杆的高度.
点拨:入射角=反射角
∵入射角=反射角,
∴∠AEB=∠CED.
∵人、旗杆都垂直于地面,
∴∠B=∠D=90°.
∴ .
因此,测量出人与镜子的距离BE,旗杆与镜子的距离DE,再知道人的身高AB,就可以求出旗杆CD的高度.
方法三:利用标杆测量旗杆的高度
操作方法:选一名学生为观测者,在他和旗杆之间的地面上直立一根高度已知的标杆,观测者前后调整自己的位置,使旗杆顶部、标杆顶部与眼睛恰好在同一直线上时,分别测出他的脚与旗杆底部,以及标杆底部的距离即可求出旗杆的高度.
点拨:人、标杆和旗杆都垂直于地面.
∵人、标杆和旗杆都垂直于地面,
∴∠ABF=∠EFD=∠CDH=90°,
∴人、标杆和旗杆是互相平行的.
∵EF∥CN,∴∠1=∠2.
∵∠3=∠3,△AME∽△ANC,
∴ .
∵人与标杆的距离、人与旗杆的距离,标杆与人的身高的差EM都已测量出,
∴能求出CN.
∵∠ABF=∠CDF=∠AND=90°,
∴四边形ABND为矩形.
∴DN=AB.
∴能求出旗杆CD的长度.
如图,测得BD=120 m,DC=60 m,EC=50 m,求河宽AB.
四、运用提高
100 m.
谈谈你在本节课的收获.
五、课堂小结
1.必做题:
教材第55,56页习题27.2第10、11题.
2.选做题:
教材第56页习题27.2第16题.
六、布置作业
3.备选题:
一盗窃犯于夜深人静之时潜入某单位作案,该单位的自动摄像系统摄下了他作案的全过程.请你为警方设计一个方案,估计该盗窃犯的大致身高.
再见!
