27.2.3相似三角形应用1 课件(共12张PPT)
文档属性
| 名称 | 27.2.3相似三角形应用1 课件(共12张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 140.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-10 00:00:00 | ||
图片预览




文档简介
(共12张PPT)
第二十七章 相 似
27.2.3 相似三角形应用举例(1)
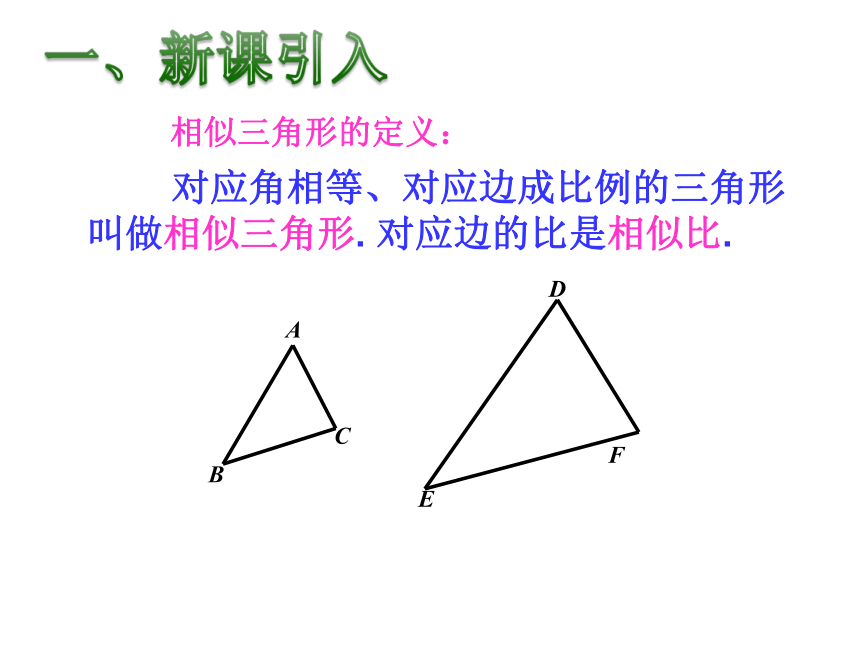
对应角相等、对应边成比例的三角形叫做相似三角形. 对应边的比是相似比.
A
B
C
E
D
F
相似三角形的定义:
一、新课引入
相似三角形的判定方法
通过定义
平行于三角形一边的直线
三边对应成比例
两边对应成比例且夹角相等
两角对应相等
两直角三角形的斜边和一条直角边对应成比例
(三边对应成比例,三角相等)
(SSS)
(AA)
(SAS)
(HL)
讨论:
利用三角形的相似如何解决一些不能直接测量的物体的长度问题?
相似三角形对应边的比相等.
四条对应边中若已知三条则可求第四条.
二、提出问题
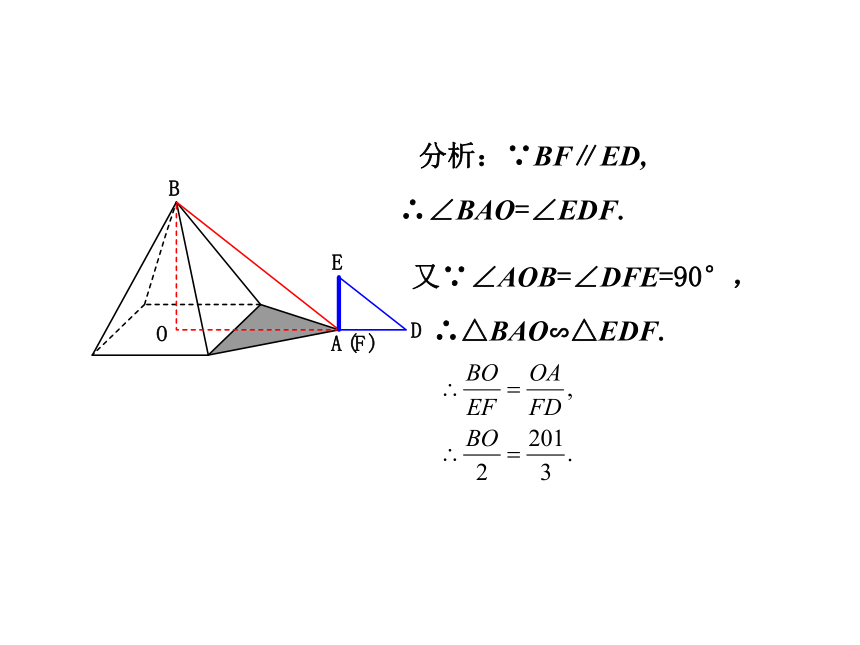
例3 据史料记载,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.
如图1,如果木杆EF长2 m,它的影长FD为3 m,测得OA为201 m,求金字塔的高度BO.
图1
三、小试牛刀
分析:∵BF∥ED,
∴∠BAO=∠EDF.
又∵∠AOB=∠DFE=90°,
∴△BAO∽△EDF.
例4 如图2,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45 m,ST=90 m,QR=60 m,求河的宽度PQ.
四、渐入佳境
图2
解:根据题意得出:QR∥ST,
则△PQR∽△PST,
解得:PQ=90(m)
在某一时刻,测得一根高为1.8 m的竹竿的影子长为3 m,同时测得一栋高楼的影长为90 m,这栋高楼的高度是多少?
五、运用提高
54m.
说说你在本节课的收获.
六、课堂小结
1.必做题:
教材第55页习题27.2第9题.
2.选做题:
教材第56页习题27.2第15题.
七、布置作业
再见!
第二十七章 相 似
27.2.3 相似三角形应用举例(1)
对应角相等、对应边成比例的三角形叫做相似三角形. 对应边的比是相似比.
A
B
C
E
D
F
相似三角形的定义:
一、新课引入
相似三角形的判定方法
通过定义
平行于三角形一边的直线
三边对应成比例
两边对应成比例且夹角相等
两角对应相等
两直角三角形的斜边和一条直角边对应成比例
(三边对应成比例,三角相等)
(SSS)
(AA)
(SAS)
(HL)
讨论:
利用三角形的相似如何解决一些不能直接测量的物体的长度问题?
相似三角形对应边的比相等.
四条对应边中若已知三条则可求第四条.
二、提出问题
例3 据史料记载,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.
如图1,如果木杆EF长2 m,它的影长FD为3 m,测得OA为201 m,求金字塔的高度BO.
图1
三、小试牛刀
分析:∵BF∥ED,
∴∠BAO=∠EDF.
又∵∠AOB=∠DFE=90°,
∴△BAO∽△EDF.
例4 如图2,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45 m,ST=90 m,QR=60 m,求河的宽度PQ.
四、渐入佳境
图2
解:根据题意得出:QR∥ST,
则△PQR∽△PST,
解得:PQ=90(m)
在某一时刻,测得一根高为1.8 m的竹竿的影子长为3 m,同时测得一栋高楼的影长为90 m,这栋高楼的高度是多少?
五、运用提高
54m.
说说你在本节课的收获.
六、课堂小结
1.必做题:
教材第55页习题27.2第9题.
2.选做题:
教材第56页习题27.2第15题.
七、布置作业
再见!
