14.2.2完全平方公式(1) 课件(共25张PPT)
文档属性
| 名称 | 14.2.2完全平方公式(1) 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 929.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-09 18:26:18 | ||
图片预览








文档简介
(共25张PPT)
人教版 八年级上册
14.2.2 完全平方公式(1)
课件说明
教学目标:
1.理解完全平方公式,能用公式进行计算.
2.经历探索完全平方公式的过程,进而感受特殊
到一般、数形结合思想,发展符号意识和几何
直观观念.
教学重点:完全平方公式.
(a+b)(a-b) =a2-b2
乘法的平方差公式.
两个数的和与这两个数的差的积,
等于这两个数的平方差.
复习旧知
计算:(1)(5+x)(5-x) = .
25-x2
(2)20222-2021×2023= .
1
(4) (m-2)2= .
计算下列各式:
(1) (p+1)2= ;
p2 +2p+ 1
(2) (m+2)2= ;
(3) (p-1)2= ;
你能发现什么规律?
m2 +4m+ 4
m2 -4m+ 4
p2 -2p+ 1
= (p+1)(p+1)
=
p2
+p
+p
+1
(p+1)2
探究新知
(4) (m-2)2= .
(1) (p+1)2= ;
p2 +2p+ 1
(2) (m+2)2= ;
(3) (p-1)2= ;
m2 +4m+ 4
m2 -4m+ 4
p2 -2p+ 1
你能用式子表示发现的规律吗?
(a+b)2 =
(a-b)2 =
a2+2ab+b2
a2-2ab+b2
探究新知
你能用文字语言表述所发现的规律吗?
(a+b)2 =
(a-b)2 =
a2 +2ab+b2
a2 -2ab+b2
两数和的平方,
等于它们的平方和,
加上它们的积的2倍.
两数差的平方,
等于它们的平方和,
减去它们的积的2倍.
探究新知
(1)积为二次三项式;
(2)积中两项为两数的平方和;
(3)另一项是两数积的2倍,且与乘式中间的符号相同;
(4)公式中的字母a,b 可以表示数,单项式和多项式.
(a+b)2 =
(a-b)2 =
a2 +2ab+b2
a2 -2ab+b2
公式特点:
完全平方公式
学习新知
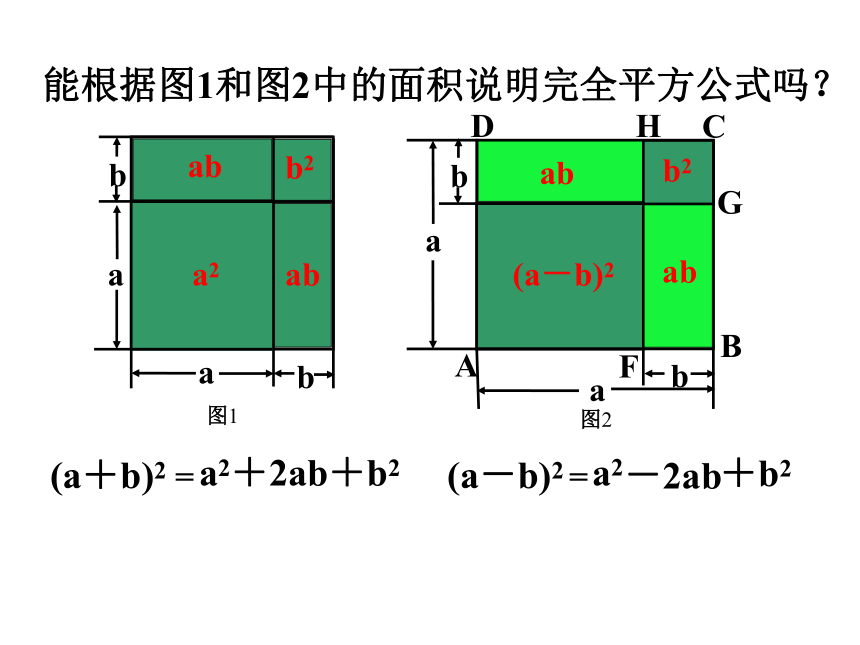
能根据图1和图2中的面积说明完全平方公式吗?
b
b
a
a
图1
图2
b
a
a
D
E
A
H
M
C
G
B
F
b
(a+b)2 =
(a-b)2 =
a2+2ab+b2
a2
a2
b2
ab
ab
ab
(a-b)2
-2ab
ab
b2
+b2
(1) (a+b)2 与
(-a-b)2 相等吗?
(2) (a-b)2 与
(b-a)2 相等吗?
(3) (a-b)2 与
a2- b2 相等吗?
(a+b)2 =
(-a-b)2 .
(a-b)2 =
(b-a)2
(a-b)2 ≠
a2 -b2
练习巩固
下面各式的计算对不对?如果不对,应当怎样改正?
(1) (x+y)2 = x2+y2;
(2) (x-y)2 = x2-y2;
(3) (x-y)2 = x2+2xy+y2;
(4) (x+y)2 = x2+xy+y2.
( )
( )
( )
( )
×
×
×
×
练习巩固
例1 运用完全平方公式计算:
(1) (4m+n)2 ;
(2) (y- )2 .
1
2
解:
=
(1) (4m+n)2
(4m)2
+n2
+2 4m n
●
●
=
16m2+8mn+n2
(2) (y- )2
=
y2
-2 y
●
●
+( )2
=
y2 -y+
1
2
1
2
1
2
1
4
例题解析
例2 运用完全平方公式计算:
(1) 1022 ;
(2) 992 .
解:(1) 1022 = (100+2)2
(2)992= (100-1)2
=
=
=
=
=
=
1002
+2 100 2
●
●
+22
10000
+400
+4
10404
1002
10000
-200
+1
9801
+12
-2 100 1
●
●
例题解析
计算:
(1) (x+6)2 ;
(3) (3+x)2 ;
(2) (y-5)2 ;
(4) (2-y)2 .
=
x2+12x+36
=
y2-10y+25
=
9+6x+x2
=
4-4y+y2
练习巩固
计算:
(1) (-2x+5)2 ;
(3) (-3x+2y)2 ;
(2) (-2x-5)2 ;
(4) (3x-2y)2 .
=
4x2-20x+25
=
4x2+20x+25
=
9x2-12xy+4y2
=
9x2-12xy+4y2
练习巩固
(1) (x+ )2 ;
(2) (x- )2 ;
(3) (-3+ )2 ;
(4) ( x- y)2 .
计算:
1
2
y
2
x
3
3
4
2
3
练习巩固
=
x2+x+
=
x2 +
●
x
●
+
( )2
(1) (x+ )2
2
=
x2-xy+ y2
=
x2 -
2
●
+
( )2
x
●
1
2
1
2
1
2
1
4
(2) (x- )2
y
2
y
2
y
2
1
4
=
=
x2-xy+ y2
9-2x+ x2
=
=
(-3)2 +
2
●
●
+
( )2
(-3)
( )2
-
2
●
●
+
( )2
(3) (-3+ )2
x
3
1
9
x
3
x
3
(4) ( x- y)2
3
4
2
3
3
4
x
2
3
y
3
4
x
2
3
y
4
9
9
16
(1)本节课学习了哪些主要内容?
(2)完全平方公式结构有什么特点?
课堂小结
1. 下列多项式中,是完全平方式的是( ).
A.m2-2mn +n2 B.
C. D.
巩固提高
x2+4xy+4y2
x2-2xy-y2
25a2+10ab-b2
2. 计算(2x-y)(-y+2x)的结果是( ).
A.4x2-4xy +y2 B.x2+4xy+4y2
C.2x2 - y2 D.4x2-y2
B
A
4.如果(5x+3y)2= (5x-3y)2+ M,那么M表示
的式子是( ).
A.30xy B.60xy C.12xy D.15xy
3.如果x2 +(m+1)x+9是一个完全平方式,
那么m的值是( ).
A. ±6 B.5 C.-7 D.5或-7
D
B
5.图(1)是一个长为2m,宽为2n(m>n)的长
方形,用剪刀沿图中虚线(对称轴)剪开,
把它分成四块形状和大小都一样的小长方
形,然后按图(2)那样拼成一个正方形,则
中间空的部分的面积是( ).
A.2mn
B.(m+n)2
C.(m-n)2
D. m2-n2
图(1)
图(2)
C
6.先化简,再求值:
(x+1)(x-1)-(2-x)2,其中x= 2022.
解:
(x+1)(x-1 )- (2-x)2
=x2-1 - (4-4x+x2)
=x2-1 -4 +4x -x2
当x= 2022时,
原式=4× 2022-5=8083.
=4x -5
今天作业
课本P112页第2、5、6题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 八年级上册
14.2.2 完全平方公式(1)
课件说明
教学目标:
1.理解完全平方公式,能用公式进行计算.
2.经历探索完全平方公式的过程,进而感受特殊
到一般、数形结合思想,发展符号意识和几何
直观观念.
教学重点:完全平方公式.
(a+b)(a-b) =a2-b2
乘法的平方差公式.
两个数的和与这两个数的差的积,
等于这两个数的平方差.
复习旧知
计算:(1)(5+x)(5-x) = .
25-x2
(2)20222-2021×2023= .
1
(4) (m-2)2= .
计算下列各式:
(1) (p+1)2= ;
p2 +2p+ 1
(2) (m+2)2= ;
(3) (p-1)2= ;
你能发现什么规律?
m2 +4m+ 4
m2 -4m+ 4
p2 -2p+ 1
= (p+1)(p+1)
=
p2
+p
+p
+1
(p+1)2
探究新知
(4) (m-2)2= .
(1) (p+1)2= ;
p2 +2p+ 1
(2) (m+2)2= ;
(3) (p-1)2= ;
m2 +4m+ 4
m2 -4m+ 4
p2 -2p+ 1
你能用式子表示发现的规律吗?
(a+b)2 =
(a-b)2 =
a2+2ab+b2
a2-2ab+b2
探究新知
你能用文字语言表述所发现的规律吗?
(a+b)2 =
(a-b)2 =
a2 +2ab+b2
a2 -2ab+b2
两数和的平方,
等于它们的平方和,
加上它们的积的2倍.
两数差的平方,
等于它们的平方和,
减去它们的积的2倍.
探究新知
(1)积为二次三项式;
(2)积中两项为两数的平方和;
(3)另一项是两数积的2倍,且与乘式中间的符号相同;
(4)公式中的字母a,b 可以表示数,单项式和多项式.
(a+b)2 =
(a-b)2 =
a2 +2ab+b2
a2 -2ab+b2
公式特点:
完全平方公式
学习新知
能根据图1和图2中的面积说明完全平方公式吗?
b
b
a
a
图1
图2
b
a
a
D
E
A
H
M
C
G
B
F
b
(a+b)2 =
(a-b)2 =
a2+2ab+b2
a2
a2
b2
ab
ab
ab
(a-b)2
-2ab
ab
b2
+b2
(1) (a+b)2 与
(-a-b)2 相等吗?
(2) (a-b)2 与
(b-a)2 相等吗?
(3) (a-b)2 与
a2- b2 相等吗?
(a+b)2 =
(-a-b)2 .
(a-b)2 =
(b-a)2
(a-b)2 ≠
a2 -b2
练习巩固
下面各式的计算对不对?如果不对,应当怎样改正?
(1) (x+y)2 = x2+y2;
(2) (x-y)2 = x2-y2;
(3) (x-y)2 = x2+2xy+y2;
(4) (x+y)2 = x2+xy+y2.
( )
( )
( )
( )
×
×
×
×
练习巩固
例1 运用完全平方公式计算:
(1) (4m+n)2 ;
(2) (y- )2 .
1
2
解:
=
(1) (4m+n)2
(4m)2
+n2
+2 4m n
●
●
=
16m2+8mn+n2
(2) (y- )2
=
y2
-2 y
●
●
+( )2
=
y2 -y+
1
2
1
2
1
2
1
4
例题解析
例2 运用完全平方公式计算:
(1) 1022 ;
(2) 992 .
解:(1) 1022 = (100+2)2
(2)992= (100-1)2
=
=
=
=
=
=
1002
+2 100 2
●
●
+22
10000
+400
+4
10404
1002
10000
-200
+1
9801
+12
-2 100 1
●
●
例题解析
计算:
(1) (x+6)2 ;
(3) (3+x)2 ;
(2) (y-5)2 ;
(4) (2-y)2 .
=
x2+12x+36
=
y2-10y+25
=
9+6x+x2
=
4-4y+y2
练习巩固
计算:
(1) (-2x+5)2 ;
(3) (-3x+2y)2 ;
(2) (-2x-5)2 ;
(4) (3x-2y)2 .
=
4x2-20x+25
=
4x2+20x+25
=
9x2-12xy+4y2
=
9x2-12xy+4y2
练习巩固
(1) (x+ )2 ;
(2) (x- )2 ;
(3) (-3+ )2 ;
(4) ( x- y)2 .
计算:
1
2
y
2
x
3
3
4
2
3
练习巩固
=
x2+x+
=
x2 +
●
x
●
+
( )2
(1) (x+ )2
2
=
x2-xy+ y2
=
x2 -
2
●
+
( )2
x
●
1
2
1
2
1
2
1
4
(2) (x- )2
y
2
y
2
y
2
1
4
=
=
x2-xy+ y2
9-2x+ x2
=
=
(-3)2 +
2
●
●
+
( )2
(-3)
( )2
-
2
●
●
+
( )2
(3) (-3+ )2
x
3
1
9
x
3
x
3
(4) ( x- y)2
3
4
2
3
3
4
x
2
3
y
3
4
x
2
3
y
4
9
9
16
(1)本节课学习了哪些主要内容?
(2)完全平方公式结构有什么特点?
课堂小结
1. 下列多项式中,是完全平方式的是( ).
A.m2-2mn +n2 B.
C. D.
巩固提高
x2+4xy+4y2
x2-2xy-y2
25a2+10ab-b2
2. 计算(2x-y)(-y+2x)的结果是( ).
A.4x2-4xy +y2 B.x2+4xy+4y2
C.2x2 - y2 D.4x2-y2
B
A
4.如果(5x+3y)2= (5x-3y)2+ M,那么M表示
的式子是( ).
A.30xy B.60xy C.12xy D.15xy
3.如果x2 +(m+1)x+9是一个完全平方式,
那么m的值是( ).
A. ±6 B.5 C.-7 D.5或-7
D
B
5.图(1)是一个长为2m,宽为2n(m>n)的长
方形,用剪刀沿图中虚线(对称轴)剪开,
把它分成四块形状和大小都一样的小长方
形,然后按图(2)那样拼成一个正方形,则
中间空的部分的面积是( ).
A.2mn
B.(m+n)2
C.(m-n)2
D. m2-n2
图(1)
图(2)
C
6.先化简,再求值:
(x+1)(x-1)-(2-x)2,其中x= 2022.
解:
(x+1)(x-1 )- (2-x)2
=x2-1 - (4-4x+x2)
=x2-1 -4 +4x -x2
当x= 2022时,
原式=4× 2022-5=8083.
=4x -5
今天作业
课本P112页第2、5、6题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
