人教A版数学选修2-1 2.4.1 抛物线及其标准方程 课件(23张PPT)
文档属性
| 名称 | 人教A版数学选修2-1 2.4.1 抛物线及其标准方程 课件(23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-09 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
抛物线及其标准方程
学习目标
1.通过动画演示和动手操作,加深对抛物线的定义、标准方程及其中p的几何意义的理解.
2.掌握抛物线方程的四种标准形式,会用待定系数法求抛物线的标准方程.
3.掌握已知抛物线的标准方程,熟练地写出它的焦点坐标和准线方程.
线型上下导航版
情景导入
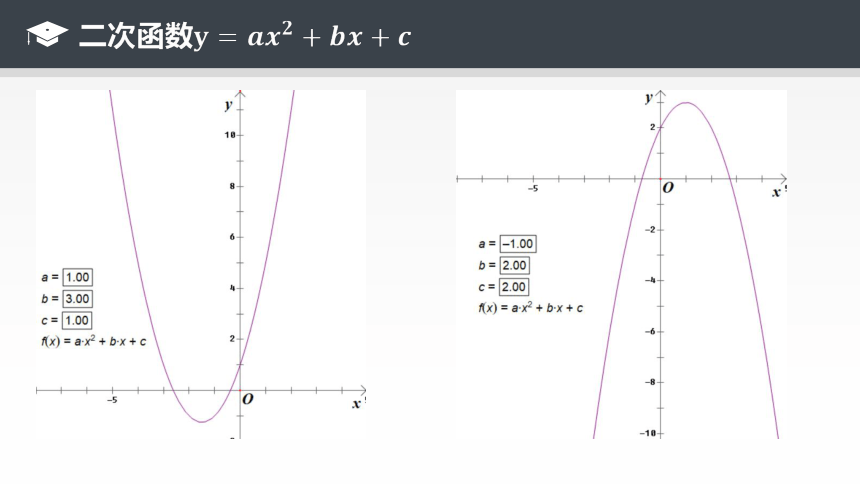
二次函数
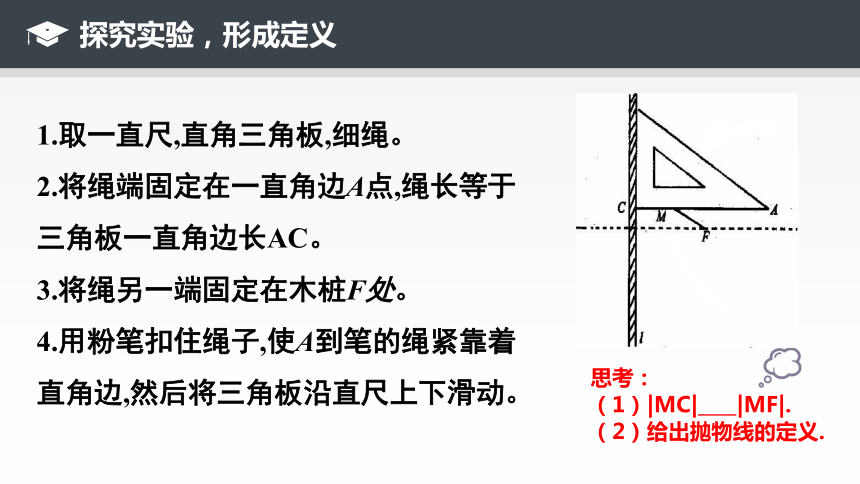
探究实验,形成定义
思考:
(1)|MC|____|MF|.
(2)给出抛物线的定义.
1.取一直尺,直角三角板,细绳。
2.将绳端固定在一直角边A点,绳长等于三角板一直角边长AC。
3.将绳另一端固定在木桩F处。
4.用粉笔扣住绳子,使A到笔的绳紧靠着直角边,然后将三角板沿直尺上下滑动。
观看动画,巩固定义
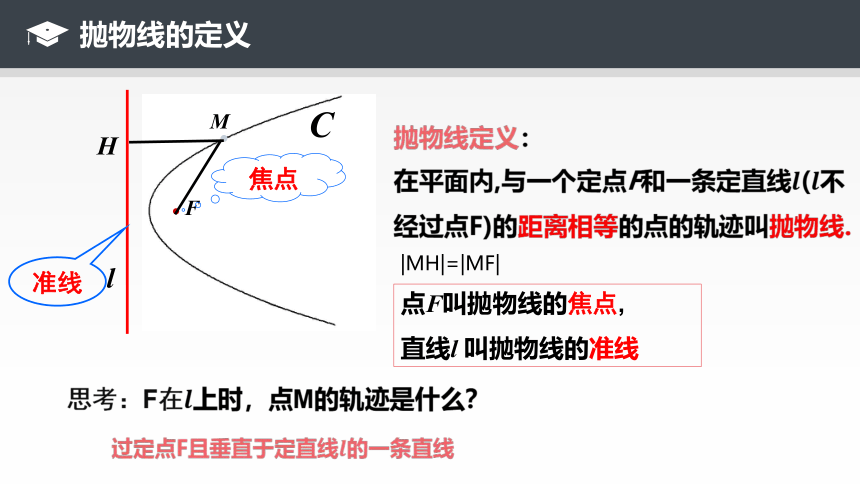
抛物线的定义
|MH|=|MF|
抛物线定义:
在平面内,与一个定点F和一条定直线(不经过点F)的距离相等的点的轨迹叫抛物线.
过定点F且垂直于定直线的一条直线
M
·
F
l
·
焦点
准线
点F叫抛物线的焦点,
直线l 叫抛物线的准线
思考:F在上时,点M的轨迹是什么?
化 简
列 式
设 点
建 系
以过点F且垂直于直线 l 的直线为x轴,垂足为K.以FK的中点O为坐标原点建立直角坐标系xOy.
F
M
设M(x,y)是抛物线上任意一点,
点M到l的距离为d.
x
K
y
O
l
·
·
·
(x,y)
H
d
由抛物线的定义,抛物线就是点的集合
(p>0),
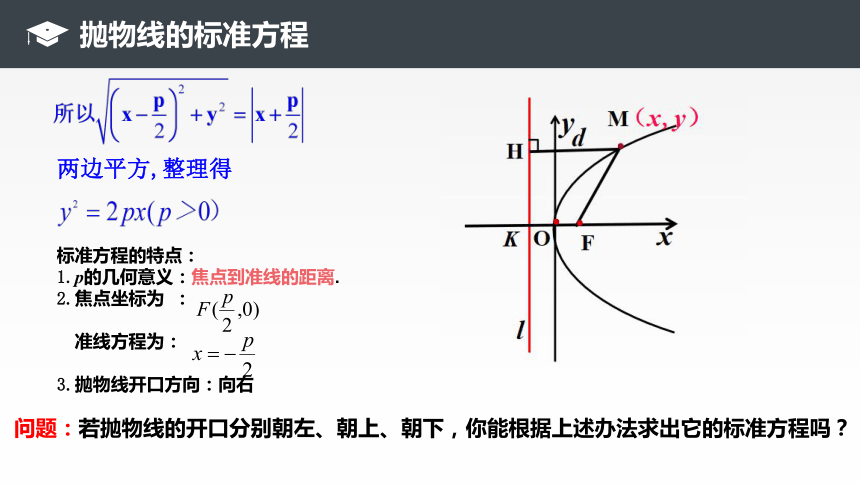
抛物线的标准方程
两边平方,整理得
M
抛物线的标准方程
标准方程的特点:
1.p的几何意义:焦点到准线的距离.
2.焦点坐标为 :
准线方程为:
3.抛物线开口方向:向右
问题:若抛物线的开口分别朝左、朝上、朝下,你能根据上述办法求出它的标准方程吗?
抛物线四种标准方程(教材P66探究)
标准方程 (>0)
图像
焦点坐标 () () (-) ()
准线方程 =- =- = =
开口方向 右 上 左 下
焦点位置判断 看指数,谁是1,在谁上。 归纳:
方程的特点:
1.左边是二次式,右边是一次式
2.一次项系数是焦点横坐标的4倍
自问自解
×
√
×
×
√
互问合解
例1:根据下列条件分别求出抛物线的标准方程:
(1)准线方程为y=;
(2)焦点在y轴上,焦点到准线的距离为5.
(3)经过点.
求标准方程的方法
求抛物线的标准方程一般有两种形式:
(1)定义法,直接利用定义求解.
(2)待定系数法.
注意:
1.若已知抛物线的焦点位置,则可设出抛物线的标准方程,求出p 值即可.
2.若抛物线的焦点位置不确定,则要分情况讨论,另外,焦点在 x 轴上的抛物线方程统一设成 y2=ax (a ≠ 0) ,焦点在 y 轴上的抛物线方程可统一设成 x2=ay (a ≠ 0).
再问深解
例2 :已知动圆M与直线y=2相切,且与定圆C:x2+(y+3)2=1外切,求动圆圆心M的轨迹方程.
解:设动圆圆心为M(x,y),半径为r,由题意可得M到C(0,-3)的距离与到直线y=3的距离相等.
由抛物线的定义可知:动圆圆心的轨迹是以C(0,-3)为焦点,以y=3为准线的一条抛物线,其方程为x2=-12y.
课堂评估
课堂评估
课堂评估
课堂评估
课堂评估
课堂评估
课堂小结
☆一个定义:我们把平面内与一个定点F和一条定直线( 不经过点F)的距离相等的点的轨迹叫做抛物线.
☆两种思想方法:“数形结合思想”、“用代数方法解决几何问题”----建系、列方程
☆三项注意:定义的前提条件、p的几何意义、标准方程的概念
☆四种形式的标准方程
作业
课本73页:习题A组1-5
谢谢!
抛物线及其标准方程
学习目标
1.通过动画演示和动手操作,加深对抛物线的定义、标准方程及其中p的几何意义的理解.
2.掌握抛物线方程的四种标准形式,会用待定系数法求抛物线的标准方程.
3.掌握已知抛物线的标准方程,熟练地写出它的焦点坐标和准线方程.
线型上下导航版
情景导入
二次函数
探究实验,形成定义
思考:
(1)|MC|____|MF|.
(2)给出抛物线的定义.
1.取一直尺,直角三角板,细绳。
2.将绳端固定在一直角边A点,绳长等于三角板一直角边长AC。
3.将绳另一端固定在木桩F处。
4.用粉笔扣住绳子,使A到笔的绳紧靠着直角边,然后将三角板沿直尺上下滑动。
观看动画,巩固定义
抛物线的定义
|MH|=|MF|
抛物线定义:
在平面内,与一个定点F和一条定直线(不经过点F)的距离相等的点的轨迹叫抛物线.
过定点F且垂直于定直线的一条直线
M
·
F
l
·
焦点
准线
点F叫抛物线的焦点,
直线l 叫抛物线的准线
思考:F在上时,点M的轨迹是什么?
化 简
列 式
设 点
建 系
以过点F且垂直于直线 l 的直线为x轴,垂足为K.以FK的中点O为坐标原点建立直角坐标系xOy.
F
M
设M(x,y)是抛物线上任意一点,
点M到l的距离为d.
x
K
y
O
l
·
·
·
(x,y)
H
d
由抛物线的定义,抛物线就是点的集合
(p>0),
抛物线的标准方程
两边平方,整理得
M
抛物线的标准方程
标准方程的特点:
1.p的几何意义:焦点到准线的距离.
2.焦点坐标为 :
准线方程为:
3.抛物线开口方向:向右
问题:若抛物线的开口分别朝左、朝上、朝下,你能根据上述办法求出它的标准方程吗?
抛物线四种标准方程(教材P66探究)
标准方程 (>0)
图像
焦点坐标 () () (-) ()
准线方程 =- =- = =
开口方向 右 上 左 下
焦点位置判断 看指数,谁是1,在谁上。 归纳:
方程的特点:
1.左边是二次式,右边是一次式
2.一次项系数是焦点横坐标的4倍
自问自解
×
√
×
×
√
互问合解
例1:根据下列条件分别求出抛物线的标准方程:
(1)准线方程为y=;
(2)焦点在y轴上,焦点到准线的距离为5.
(3)经过点.
求标准方程的方法
求抛物线的标准方程一般有两种形式:
(1)定义法,直接利用定义求解.
(2)待定系数法.
注意:
1.若已知抛物线的焦点位置,则可设出抛物线的标准方程,求出p 值即可.
2.若抛物线的焦点位置不确定,则要分情况讨论,另外,焦点在 x 轴上的抛物线方程统一设成 y2=ax (a ≠ 0) ,焦点在 y 轴上的抛物线方程可统一设成 x2=ay (a ≠ 0).
再问深解
例2 :已知动圆M与直线y=2相切,且与定圆C:x2+(y+3)2=1外切,求动圆圆心M的轨迹方程.
解:设动圆圆心为M(x,y),半径为r,由题意可得M到C(0,-3)的距离与到直线y=3的距离相等.
由抛物线的定义可知:动圆圆心的轨迹是以C(0,-3)为焦点,以y=3为准线的一条抛物线,其方程为x2=-12y.
课堂评估
课堂评估
课堂评估
课堂评估
课堂评估
课堂评估
课堂小结
☆一个定义:我们把平面内与一个定点F和一条定直线( 不经过点F)的距离相等的点的轨迹叫做抛物线.
☆两种思想方法:“数形结合思想”、“用代数方法解决几何问题”----建系、列方程
☆三项注意:定义的前提条件、p的几何意义、标准方程的概念
☆四种形式的标准方程
作业
课本73页:习题A组1-5
谢谢!
