人教A版数学选修2-1 2.4.2抛物线的几何性质 课件(17张PPT)
文档属性
| 名称 | 人教A版数学选修2-1 2.4.2抛物线的几何性质 课件(17张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-09 08:55:33 | ||
图片预览






文档简介
(共17张PPT)
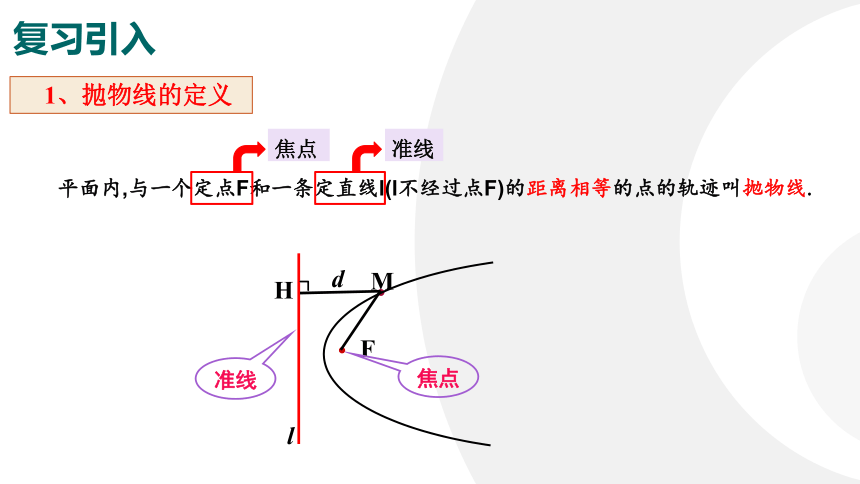
平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.
焦点
准线
1、抛物线的定义
M
·
F
l
·
d
H
准线
焦点
复习引入
图形 焦点位置 标准方程 焦点坐标 准线方程
x轴的
正半轴上
x轴的
负半轴上
y轴的
正半轴上
y轴的
负半轴上
y2=2px
(p>0)
y2=-2px
(p>0)
x2=2py
(p>0)
x2=-2py
(p>0)
2、四种抛物线及其它们的标准方程
一次变量定焦点
开口方向看正负
P的几何意义:
抛物线的焦点到准线的距离
2.4.2抛物线的几何性质(一)
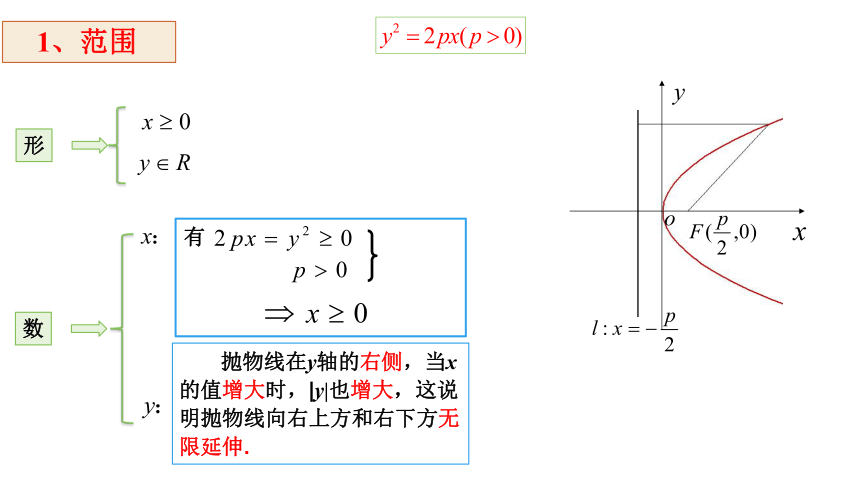
1、范围
形
数
有
抛物线在y轴的右侧,当x的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限延伸.
(x,y))
(x,-y)
2、对称性
形
数
关于x轴对称
3、顶点
顶点
抛物线与它轴的交点
抛物线的轴
定义:
4、离心率
抛物线上的点与焦点的距离和它到准线的距离之比
5、焦半径
定义:
抛物线上任意一点与焦点的连线。
x
y
O
F
P(x0,y0)
焦半径公式:
6、
四种形式抛物线的几何性质
图 形 方程 焦点 准线 焦半径 范围 顶点 对称轴 e
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2 = 2px
(p>0)
y2 = -2px
(p>0)
x2 = 2py
(p>0)
x2 = -2py
(p>0)
x≥0
y∈R
x≤0
y∈R
y≥0
x∈R
y ≤ 0
x∈R
(0,0)
x轴
y轴
1
例1 已知抛物线的对称轴在坐标轴上,以原点为顶点,且经过点M(1,-2),求抛物线方程.
例题讲解
(1)当抛物线的焦点在x轴上时,设其方程为y2=mx.
将M(1,-2)代入,得m=4, y2=4x.
(2)当抛物线的焦点在y轴上时,设其方程为x2=ny.
将M(1,-2)代入,得
解:
例2.
(1)M是抛物线y2 = 2px(p>0)上一点,若点M 的横坐标为x0,则点M到焦点的距离是 .
(2)抛物线y2=12x上与焦点的距离等于9的点的坐标是 .
7.抛物线定义的应用
例题讲解
将抛物线上的点P( x,y)到焦点F的距离转化为该点到准线的距离.
x0 + —
2
p
F
x
y
8、直线与抛物线的位置关系
相 离
无公共点
一个公共点
相 切
相 交
相 交
两个公共点
注意:有一个公共点不一定是相切
8、直线与抛物线的位置关系
联立,消y,化简
l与C的对称轴平行或重合
l与C交于一点
l与C相交
l与C有两个公共点
l与C相切
l与C有1个公共点
l与C相离
l与C没有公共点
若抛物线C与直线l只有一个公共点,则l与C相切或与C的对称轴平行或重合
直线斜率不存在时,另行讨论
8、直线与抛物线的位置关系
⑴只有一个公共点
⑵有两个公共点
⑶没有公共点
8、直线与抛物线的相交弦
联立,消y,化简
(1)交点坐标法
(2)弦长公式
x
O
y
平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.
焦点
准线
1、抛物线的定义
M
·
F
l
·
d
H
准线
焦点
复习引入
图形 焦点位置 标准方程 焦点坐标 准线方程
x轴的
正半轴上
x轴的
负半轴上
y轴的
正半轴上
y轴的
负半轴上
y2=2px
(p>0)
y2=-2px
(p>0)
x2=2py
(p>0)
x2=-2py
(p>0)
2、四种抛物线及其它们的标准方程
一次变量定焦点
开口方向看正负
P的几何意义:
抛物线的焦点到准线的距离
2.4.2抛物线的几何性质(一)
1、范围
形
数
有
抛物线在y轴的右侧,当x的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限延伸.
(x,y))
(x,-y)
2、对称性
形
数
关于x轴对称
3、顶点
顶点
抛物线与它轴的交点
抛物线的轴
定义:
4、离心率
抛物线上的点与焦点的距离和它到准线的距离之比
5、焦半径
定义:
抛物线上任意一点与焦点的连线。
x
y
O
F
P(x0,y0)
焦半径公式:
6、
四种形式抛物线的几何性质
图 形 方程 焦点 准线 焦半径 范围 顶点 对称轴 e
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2 = 2px
(p>0)
y2 = -2px
(p>0)
x2 = 2py
(p>0)
x2 = -2py
(p>0)
x≥0
y∈R
x≤0
y∈R
y≥0
x∈R
y ≤ 0
x∈R
(0,0)
x轴
y轴
1
例1 已知抛物线的对称轴在坐标轴上,以原点为顶点,且经过点M(1,-2),求抛物线方程.
例题讲解
(1)当抛物线的焦点在x轴上时,设其方程为y2=mx.
将M(1,-2)代入,得m=4, y2=4x.
(2)当抛物线的焦点在y轴上时,设其方程为x2=ny.
将M(1,-2)代入,得
解:
例2.
(1)M是抛物线y2 = 2px(p>0)上一点,若点M 的横坐标为x0,则点M到焦点的距离是 .
(2)抛物线y2=12x上与焦点的距离等于9的点的坐标是 .
7.抛物线定义的应用
例题讲解
将抛物线上的点P( x,y)到焦点F的距离转化为该点到准线的距离.
x0 + —
2
p
F
x
y
8、直线与抛物线的位置关系
相 离
无公共点
一个公共点
相 切
相 交
相 交
两个公共点
注意:有一个公共点不一定是相切
8、直线与抛物线的位置关系
联立,消y,化简
l与C的对称轴平行或重合
l与C交于一点
l与C相交
l与C有两个公共点
l与C相切
l与C有1个公共点
l与C相离
l与C没有公共点
若抛物线C与直线l只有一个公共点,则l与C相切或与C的对称轴平行或重合
直线斜率不存在时,另行讨论
8、直线与抛物线的位置关系
⑴只有一个公共点
⑵有两个公共点
⑶没有公共点
8、直线与抛物线的相交弦
联立,消y,化简
(1)交点坐标法
(2)弦长公式
x
O
y
