人教A版数学选修2-1 2.3.2 双曲线的简单几何性质 课件(31张PPT)
文档属性
| 名称 | 人教A版数学选修2-1 2.3.2 双曲线的简单几何性质 课件(31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 649.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-09 08:58:12 | ||
图片预览






文档简介
(共31张PPT)
(选修2-1)第二章 圆锥曲线与方程
2.3双曲线
2.3.2双曲线的简单几何性质
2004年夏季中国在相隔20年后再一次经历了”电荒”的考验,全国的所有大城市都在拉闸限电,我们知道电能是现代生活不可缺少的能源,于是一夜之间全国上下热电厂象竹笋一样拔地而起,而象照片中“粗烟囱”更是随处可见。
冷却通风塔
如果你是设计师你将如何设计?
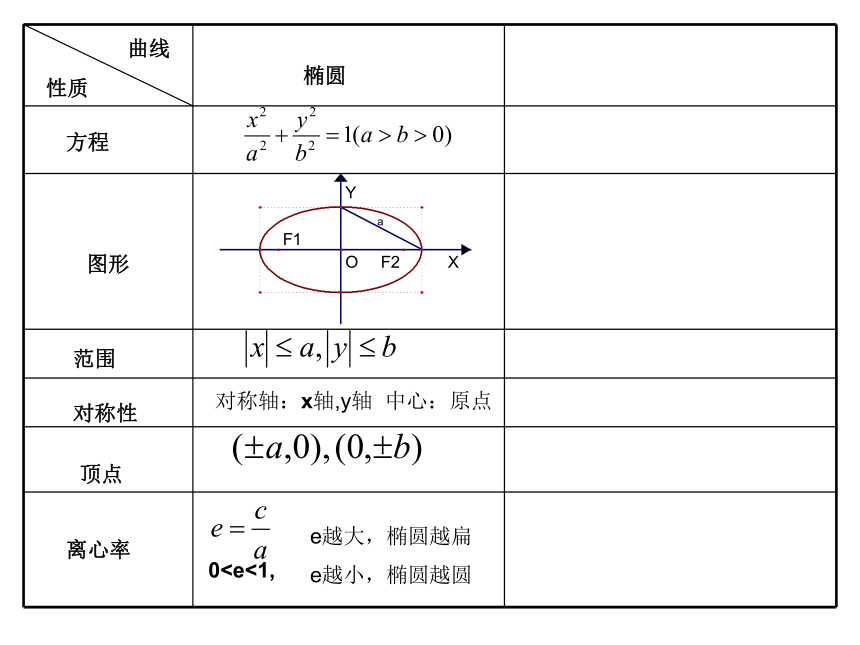
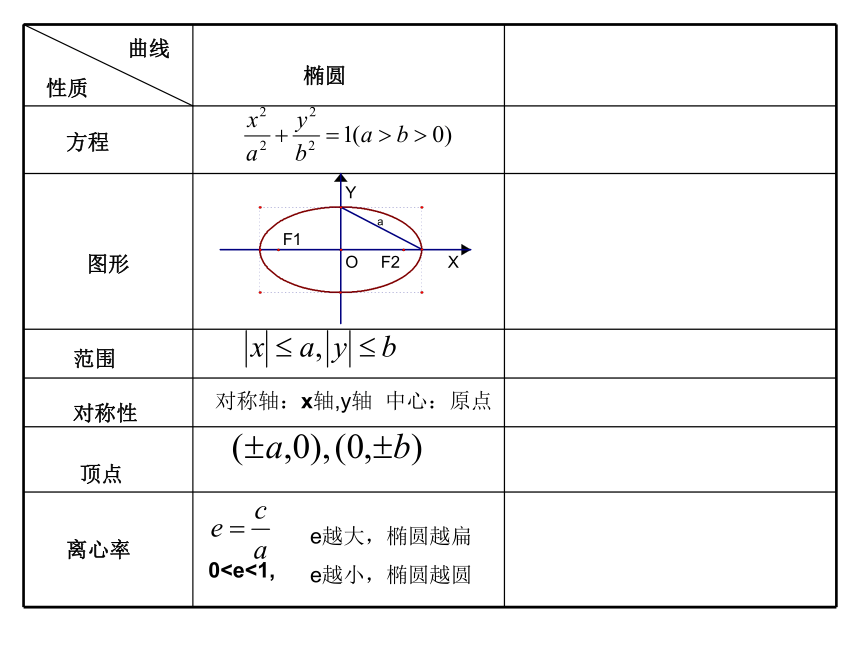
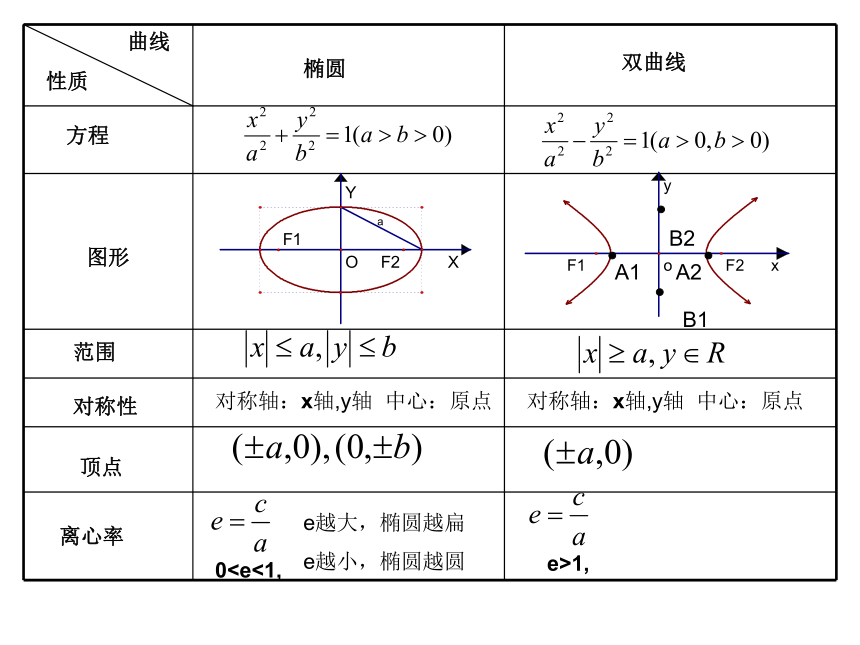
曲线
性质
方程
范围
对称性
图形
顶点
离心率
椭圆
对称轴:x轴,y轴 中心:原点
0e越大,椭圆越扁
e越小,椭圆越圆
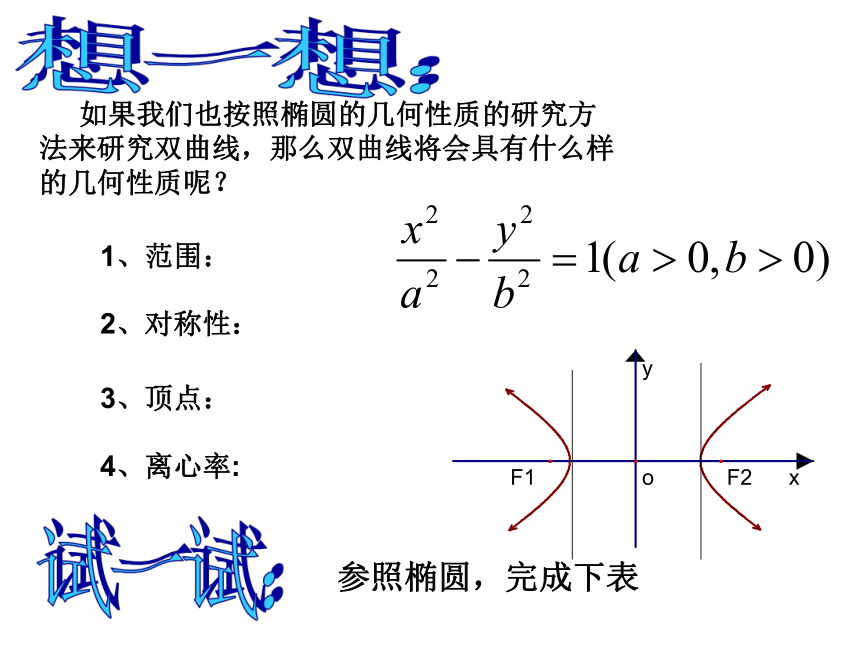
想一想:
如果我们也按照椭圆的几何性质的研究方法来研究双曲线,那么双曲线将会具有什么样的几何性质呢?
1、范围:
2、对称性:
3、顶点:
4、离心率:
试一试:
参照椭圆,完成下表
曲线
性质
方程
范围
对称性
图形
顶点
离心率
椭圆
对称轴:x轴,y轴 中心:原点
0e越大,椭圆越扁
e越小,椭圆越圆
2、对称性
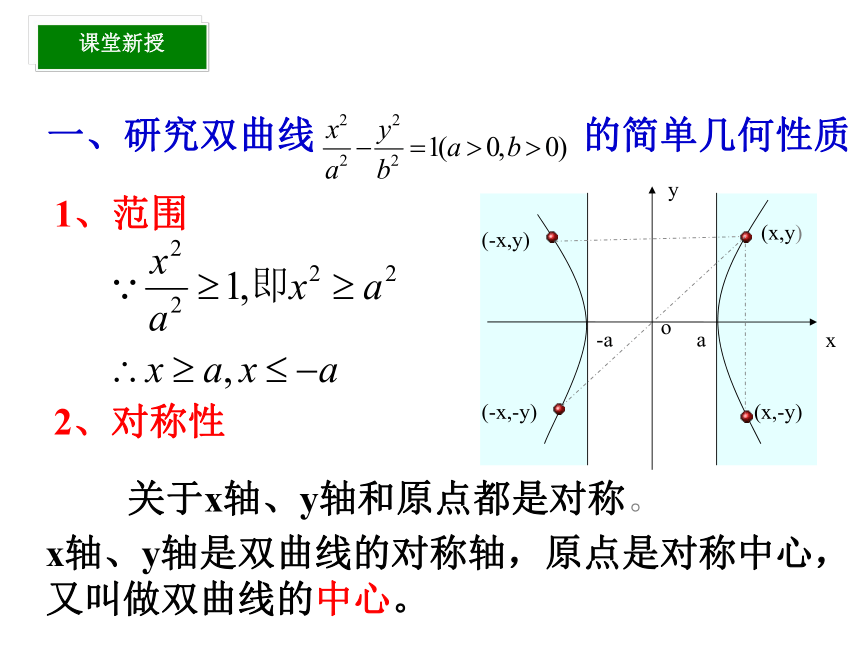
一、研究双曲线 的简单几何性质
1、范围
关于x轴、y轴和原点都是对称。
x轴、y轴是双曲线的对称轴,原点是对称中心,
又叫做双曲线的中心。
x
y
o
-a
a
(-x,-y)
(-x,y)
(x,y)
(x,-y)
课堂新授
3、顶点
(1)双曲线与对称轴的交点,叫做双曲线的顶点
x
y
o
-b
b
-a
a
如图,线段 叫做双曲线的实轴,它的长为2a,a叫做半实轴长;线段 叫做双曲线的虚轴,它的长为2b,b叫做双曲线的半虚轴长
(2)
实轴与虚轴等长的双曲线
叫等轴双曲线
(3)
曲线
性质
方程
范围
对称性
图形
顶点
离心率
椭圆
对称轴:x轴,y轴 中心:原点
0e越大,椭圆越扁
e越小,椭圆越圆
双曲线
对称轴:x轴,y轴 中心:原点
e>1,
A1
A2
B1
B2
思考:
椭圆的离心率可以决定椭圆的圆扁程度,那么双曲线的离心率能决定双曲线的什么几何特征呢?
x
y
o
根据以上四项性质,能较准确地画出双曲线的图形吗
练习:画出双曲线 的草图
双曲线的开口大小有没有限制 向远处伸展有没有约束范围
当x→∞时,方程近似变为 ,即双曲线上的点无限接近直线
y
B2
A1
A2
B1
x
O
b
a
M
N
Q
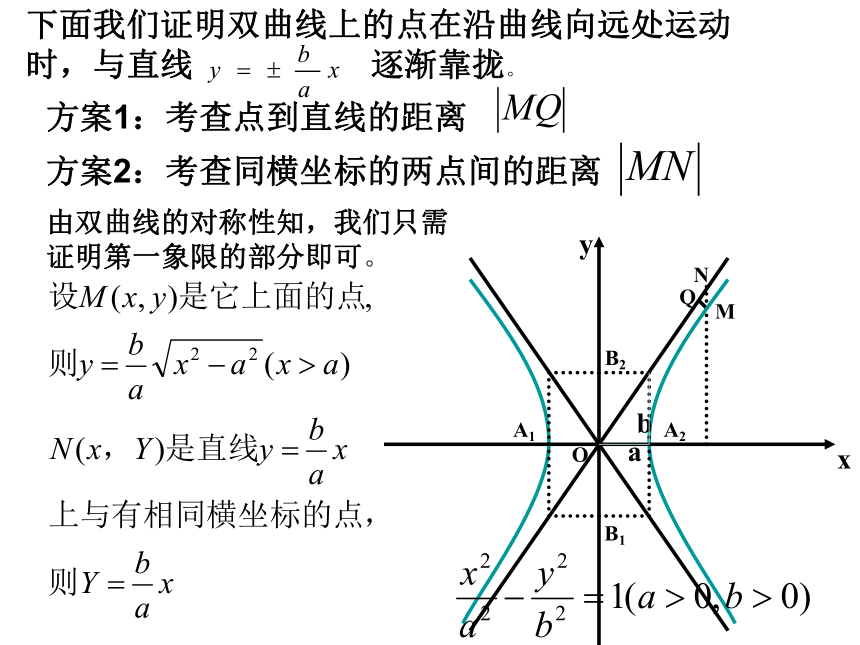
由双曲线的对称性知,我们只需证明第一象限的部分即可。
下面我们证明双曲线上的点在沿曲线向远处运动时,与直线 逐渐靠拢。
方案2:考查同横坐标的两点间的距离
方案1:考查点到直线的距离
X
M
Y
O
Q
N
(x,y)
(x,Y)
5、渐近线:
y
B2
A1
A2
B1
x
O
b
a
注:渐近线是双曲线特有的几何性质,它决定着双曲线张口的开阔与否。
离心率e与双曲线的图形变化的联系?
想一想:
x
y
B2
A1
A2
B1
O
b
a
e越大,斜率越大,倾斜角越大,张角越大,张口越开阔
e越小,斜率越小,倾斜角越小,张角越小,张口越扁狭
M(x,y)
5、渐近线
N(x,y’)
Q
慢慢靠近
x
y
o
a
b
(1)
(2)
利用渐近线可以较准确的
画出双曲线的草图
(3)
动画演示
(4)等轴双曲线的离心率e=
( 5 )
标准方程
图形
范围
对称性
顶点
焦点
离心率
渐近线
x
y
o
对称轴:x轴,y轴 中心:原点
e>1,
对称轴:x轴,y轴 中心:原点
e>1,
e越大,张口开阔
e越小,张口扁狭
e越大,张口开阔
e越小,张口扁狭
(c,0) (-c,0)
(0,c) (0,-c)
应用1:
标准方程
图形
范围
对称性
顶点
焦点
离心率
渐近线
x
y
o
对称轴:x轴,y轴 中心:原点
对称轴:x轴,y轴 中心:原点
(0,5) (0,-5)
(5,0) (-5,0)
应用2:
双曲线型自然通风塔的外形,是双曲线的一部分
绕其虚轴旋转所成的曲面(如图),它的最小
半径为12米,被旋转的双曲线的离心率为 ,
请选择适当的坐标系,求出双曲线的方程。
A
x
y
o
解:
如图建立冷却塔的轴截面所在平面的直角坐标系xoy,使最小圆的直径在x轴上,圆心与原点重合,则A(12,0)
1、若双曲线的渐近线方程为 则双曲线的离心率为 。
2、若双曲线的离心率为2,则两条渐近线的夹角为 。
课堂练习
课本61页练习2 和3
λ>0表示焦点在x轴上的双曲线;
λ<0表示焦点在y轴上的双曲线。
“共渐近线”的双曲线的应用
例3 :求下列双曲线的标准方程:
例题讲解
法二:巧设方程,运用待定系数法.
⑴设双曲线方程为 ,
法二:设双曲线方程为
∴ 双曲线方程为
∴ ,
解之得k=4,
小结:
1、本节课所研究的双曲线的几何性质有哪些?
2 、思想方法:
4. 求与椭圆
有共同焦点,渐近线方程为
的双曲线方程。
解:
椭圆的焦点在x轴上,且坐标为
双曲线的渐近线方程为
解出
作业:《作业本》34-35
谢谢!
再见!
(选修2-1)第二章 圆锥曲线与方程
2.3双曲线
2.3.2双曲线的简单几何性质
2004年夏季中国在相隔20年后再一次经历了”电荒”的考验,全国的所有大城市都在拉闸限电,我们知道电能是现代生活不可缺少的能源,于是一夜之间全国上下热电厂象竹笋一样拔地而起,而象照片中“粗烟囱”更是随处可见。
冷却通风塔
如果你是设计师你将如何设计?
曲线
性质
方程
范围
对称性
图形
顶点
离心率
椭圆
对称轴:x轴,y轴 中心:原点
0
e越小,椭圆越圆
想一想:
如果我们也按照椭圆的几何性质的研究方法来研究双曲线,那么双曲线将会具有什么样的几何性质呢?
1、范围:
2、对称性:
3、顶点:
4、离心率:
试一试:
参照椭圆,完成下表
曲线
性质
方程
范围
对称性
图形
顶点
离心率
椭圆
对称轴:x轴,y轴 中心:原点
0
e越小,椭圆越圆
2、对称性
一、研究双曲线 的简单几何性质
1、范围
关于x轴、y轴和原点都是对称。
x轴、y轴是双曲线的对称轴,原点是对称中心,
又叫做双曲线的中心。
x
y
o
-a
a
(-x,-y)
(-x,y)
(x,y)
(x,-y)
课堂新授
3、顶点
(1)双曲线与对称轴的交点,叫做双曲线的顶点
x
y
o
-b
b
-a
a
如图,线段 叫做双曲线的实轴,它的长为2a,a叫做半实轴长;线段 叫做双曲线的虚轴,它的长为2b,b叫做双曲线的半虚轴长
(2)
实轴与虚轴等长的双曲线
叫等轴双曲线
(3)
曲线
性质
方程
范围
对称性
图形
顶点
离心率
椭圆
对称轴:x轴,y轴 中心:原点
0
e越小,椭圆越圆
双曲线
对称轴:x轴,y轴 中心:原点
e>1,
A1
A2
B1
B2
思考:
椭圆的离心率可以决定椭圆的圆扁程度,那么双曲线的离心率能决定双曲线的什么几何特征呢?
x
y
o
根据以上四项性质,能较准确地画出双曲线的图形吗
练习:画出双曲线 的草图
双曲线的开口大小有没有限制 向远处伸展有没有约束范围
当x→∞时,方程近似变为 ,即双曲线上的点无限接近直线
y
B2
A1
A2
B1
x
O
b
a
M
N
Q
由双曲线的对称性知,我们只需证明第一象限的部分即可。
下面我们证明双曲线上的点在沿曲线向远处运动时,与直线 逐渐靠拢。
方案2:考查同横坐标的两点间的距离
方案1:考查点到直线的距离
X
M
Y
O
Q
N
(x,y)
(x,Y)
5、渐近线:
y
B2
A1
A2
B1
x
O
b
a
注:渐近线是双曲线特有的几何性质,它决定着双曲线张口的开阔与否。
离心率e与双曲线的图形变化的联系?
想一想:
x
y
B2
A1
A2
B1
O
b
a
e越大,斜率越大,倾斜角越大,张角越大,张口越开阔
e越小,斜率越小,倾斜角越小,张角越小,张口越扁狭
M(x,y)
5、渐近线
N(x,y’)
Q
慢慢靠近
x
y
o
a
b
(1)
(2)
利用渐近线可以较准确的
画出双曲线的草图
(3)
动画演示
(4)等轴双曲线的离心率e=
( 5 )
标准方程
图形
范围
对称性
顶点
焦点
离心率
渐近线
x
y
o
对称轴:x轴,y轴 中心:原点
e>1,
对称轴:x轴,y轴 中心:原点
e>1,
e越大,张口开阔
e越小,张口扁狭
e越大,张口开阔
e越小,张口扁狭
(c,0) (-c,0)
(0,c) (0,-c)
应用1:
标准方程
图形
范围
对称性
顶点
焦点
离心率
渐近线
x
y
o
对称轴:x轴,y轴 中心:原点
对称轴:x轴,y轴 中心:原点
(0,5) (0,-5)
(5,0) (-5,0)
应用2:
双曲线型自然通风塔的外形,是双曲线的一部分
绕其虚轴旋转所成的曲面(如图),它的最小
半径为12米,被旋转的双曲线的离心率为 ,
请选择适当的坐标系,求出双曲线的方程。
A
x
y
o
解:
如图建立冷却塔的轴截面所在平面的直角坐标系xoy,使最小圆的直径在x轴上,圆心与原点重合,则A(12,0)
1、若双曲线的渐近线方程为 则双曲线的离心率为 。
2、若双曲线的离心率为2,则两条渐近线的夹角为 。
课堂练习
课本61页练习2 和3
λ>0表示焦点在x轴上的双曲线;
λ<0表示焦点在y轴上的双曲线。
“共渐近线”的双曲线的应用
例3 :求下列双曲线的标准方程:
例题讲解
法二:巧设方程,运用待定系数法.
⑴设双曲线方程为 ,
法二:设双曲线方程为
∴ 双曲线方程为
∴ ,
解之得k=4,
小结:
1、本节课所研究的双曲线的几何性质有哪些?
2 、思想方法:
4. 求与椭圆
有共同焦点,渐近线方程为
的双曲线方程。
解:
椭圆的焦点在x轴上,且坐标为
双曲线的渐近线方程为
解出
作业:《作业本》34-35
谢谢!
再见!
