沪科版九年级上册 21.2.3-二次函数y=a(x-h)2的图象和性质 课件(共17张PPT)
文档属性
| 名称 | 沪科版九年级上册 21.2.3-二次函数y=a(x-h)2的图象和性质 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 471.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-08 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
二次函数y=a(x+h)2 的图象和性质
y=ax2+k a>0 a<0
开口方向
对称性
顶点
增减性
二次函数y=ax2+k的性质
开口向上
开口向下
关于y轴对称
(0,k)
x=0时,y最小值= k
x=0时,y最大值= k
当x<0时,
y随着x的增大而减小。
当x>0时,
y随着x的增大而增大。
当x<0时,
y随着x的增大而增大。
当x>0时,
y随着x的增大而减小。
说出下列二次函数的开口方向、对称轴及顶点坐标
(1) y=5x2
(2) y=-3x2 +2
(3) y=8x2+6
(4) y= -x2-4
向上,y轴 (0, 0)
向下,y轴 (0, 2)
向上,y轴 (0, 6)
向下,y轴 (0, - 4)
说一说下列二次函数图像之间的关系。
和
和
和
⑴
⑵
⑶
下面我们探究二次函数 y = a﹙x+h﹚2的图
像和性质,以及与y=ax2的联系与区别.
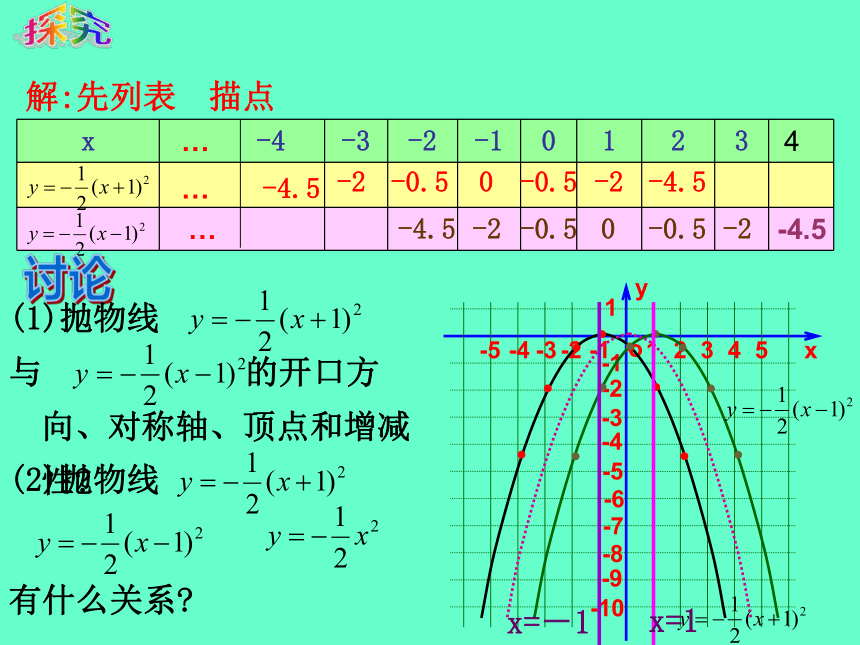
画出二次函数 、 的图像,并考虑它们的开口方向、对称轴和顶点.:
x -4 -3 -2 -1 0 1 2 3
解:先列表
描点
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
-2
…
0
-0.5
-2
-0.5
-4.5
-2
-0.5
0
-4.5
-2
-0.5
x=-1
抛物线
与 的开口方向、对称轴、顶点和增减性
(2)抛物线
有什么关系
…
4
…
-4.5
-4.5
x=1
与抛物线
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
向左平移1个单位
向右平移1个单位
即:
抛物线
、
有什么关系?
顶点(0,0)
顶点(2,0)
直线x=-2
直线x=2
向右平移2个单位
向左平移2个单位
顶点(-2,0)
对称轴:y轴
即直线: x=0
在同一坐标系中作出下列二次函数:
观察三条抛物线的相互关系,并分别指出它们的开口方向,顶点,对称轴和增减性.
向右平移2个单位
向右平移2个单位
向左平移2个单位
向左平移2个单位
一般地,抛物线y=a(x+h)2有如下特点:
(1)对称轴是x=-h;
(2)顶点是(-h,0).
(3)抛物线y=a(x+h)2可以由抛物线y=ax2向左或向右平移|h|得到.
h>0,向左平移;
h<0,向右平移
x
y
y=a(x+h)2(a≠0) a>0 a<0
开口方向
顶点坐标
对称轴
增
减
性
最值
向上
向下
(-h ,0)
(-h ,0)
当x<-h时,
y随着x的增大而减小。
当x>-h时,
y随着x的增大而增大。
当x<-h时,
y随着x的增大而增大。
当x>-h时,
y随着x的增大而减小。
x=-h时,y最小值= 0
x=-h时,y最大值= 0
二次函数y=a(x+h)2的性质
直线x=-h
直线x=-h
例1. 填空题
(1)二次函数y=2(x+5)2的图像是 ,开 口 ,对称轴是 ,当x= 时,y有最 值,是 .
(2)二次函数y=-3(x-4)2的图像是由抛物线y= -3x2 向 平移 个单位得到的;开口 ,对称轴是 ,当x= 时,y有最 值,是 .
抛物线
向上
直线x= -5
-5
小
0
右
4
向下
直线x= 4
4
大
0
(3)将二次函数y=2x2的图像向右平移3个单位后得到函数 的图像,其对称轴是 ,顶点是 ,当x 时,y随x的增大而增大;当x 时,y随x的增大而减小. (4)将二次函数y= -3(x-2)2的图像向左平移3个单位后得到函数 的图像,其顶点坐标是 ,对称轴是 ,当x= 时,y有最 值,是 .
y=2(x-3)2
直线x=3
(3,0)
>3
<3
y= -3(x+1)2
(-1,0)
直线x=-1
-1
大
0
2、y= 2(x+3)2
1、说出下列抛物线的开口方向、对称轴、顶点,最大值或最小值各是什么及增减性如何?
1、y= 2(x-3)2
3、y= 2(x-2)2
4、y= 3(x+1)2
2、若将抛物线y=-2(x-2)2的图象的顶点移到原点,则下列平移方法正确的是( )
A、向上平移2个单位
B、向下平移2个单位
C、向左平移2个单位
D、向右平移2个单位
C
3、二次函数 图像的对称轴是( )
(A)直线x=2 (B)直线x=-2
(C)y轴 (D)x轴
4、将抛物线 向左平移3个单位所得的抛物线的函数关系式为( )
A、 B、
C、 D、
5、抛物线 是由抛物线 向 平移 个单位得到的,平称后的抛物线对称轴是 ,顶点坐标是 ,当x= 时,y有最 值,其值是 。
A
D
y=-X2
右
1
直线x=1
(1,0)
1
大
0
6、抛物线y=4(x-3)2的开口方向 ,对称轴是 ,顶点坐标是 ,抛物线是最 点,
当x= 时,y有最 值,其值为 。
抛物线与x轴交点坐标 ,与y轴交点坐标 。
向上
直线x=3
(3,0)
低
3
小
0
(3,0)
(0,36)
7、求形状与y=-2(x+3)2的图象形状相同,但开口方向不同,顶点坐标是(1,0)的抛物线解析式。
小结 拓展
你认为今天这节课最需要掌握的是 ________________ ?
二次函数y=a(x+h)2 的图象和性质
y=ax2+k a>0 a<0
开口方向
对称性
顶点
增减性
二次函数y=ax2+k的性质
开口向上
开口向下
关于y轴对称
(0,k)
x=0时,y最小值= k
x=0时,y最大值= k
当x<0时,
y随着x的增大而减小。
当x>0时,
y随着x的增大而增大。
当x<0时,
y随着x的增大而增大。
当x>0时,
y随着x的增大而减小。
说出下列二次函数的开口方向、对称轴及顶点坐标
(1) y=5x2
(2) y=-3x2 +2
(3) y=8x2+6
(4) y= -x2-4
向上,y轴 (0, 0)
向下,y轴 (0, 2)
向上,y轴 (0, 6)
向下,y轴 (0, - 4)
说一说下列二次函数图像之间的关系。
和
和
和
⑴
⑵
⑶
下面我们探究二次函数 y = a﹙x+h﹚2的图
像和性质,以及与y=ax2的联系与区别.
画出二次函数 、 的图像,并考虑它们的开口方向、对称轴和顶点.:
x -4 -3 -2 -1 0 1 2 3
解:先列表
描点
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
-2
…
0
-0.5
-2
-0.5
-4.5
-2
-0.5
0
-4.5
-2
-0.5
x=-1
抛物线
与 的开口方向、对称轴、顶点和增减性
(2)抛物线
有什么关系
…
4
…
-4.5
-4.5
x=1
与抛物线
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
向左平移1个单位
向右平移1个单位
即:
抛物线
、
有什么关系?
顶点(0,0)
顶点(2,0)
直线x=-2
直线x=2
向右平移2个单位
向左平移2个单位
顶点(-2,0)
对称轴:y轴
即直线: x=0
在同一坐标系中作出下列二次函数:
观察三条抛物线的相互关系,并分别指出它们的开口方向,顶点,对称轴和增减性.
向右平移2个单位
向右平移2个单位
向左平移2个单位
向左平移2个单位
一般地,抛物线y=a(x+h)2有如下特点:
(1)对称轴是x=-h;
(2)顶点是(-h,0).
(3)抛物线y=a(x+h)2可以由抛物线y=ax2向左或向右平移|h|得到.
h>0,向左平移;
h<0,向右平移
x
y
y=a(x+h)2(a≠0) a>0 a<0
开口方向
顶点坐标
对称轴
增
减
性
最值
向上
向下
(-h ,0)
(-h ,0)
当x<-h时,
y随着x的增大而减小。
当x>-h时,
y随着x的增大而增大。
当x<-h时,
y随着x的增大而增大。
当x>-h时,
y随着x的增大而减小。
x=-h时,y最小值= 0
x=-h时,y最大值= 0
二次函数y=a(x+h)2的性质
直线x=-h
直线x=-h
例1. 填空题
(1)二次函数y=2(x+5)2的图像是 ,开 口 ,对称轴是 ,当x= 时,y有最 值,是 .
(2)二次函数y=-3(x-4)2的图像是由抛物线y= -3x2 向 平移 个单位得到的;开口 ,对称轴是 ,当x= 时,y有最 值,是 .
抛物线
向上
直线x= -5
-5
小
0
右
4
向下
直线x= 4
4
大
0
(3)将二次函数y=2x2的图像向右平移3个单位后得到函数 的图像,其对称轴是 ,顶点是 ,当x 时,y随x的增大而增大;当x 时,y随x的增大而减小. (4)将二次函数y= -3(x-2)2的图像向左平移3个单位后得到函数 的图像,其顶点坐标是 ,对称轴是 ,当x= 时,y有最 值,是 .
y=2(x-3)2
直线x=3
(3,0)
>3
<3
y= -3(x+1)2
(-1,0)
直线x=-1
-1
大
0
2、y= 2(x+3)2
1、说出下列抛物线的开口方向、对称轴、顶点,最大值或最小值各是什么及增减性如何?
1、y= 2(x-3)2
3、y= 2(x-2)2
4、y= 3(x+1)2
2、若将抛物线y=-2(x-2)2的图象的顶点移到原点,则下列平移方法正确的是( )
A、向上平移2个单位
B、向下平移2个单位
C、向左平移2个单位
D、向右平移2个单位
C
3、二次函数 图像的对称轴是( )
(A)直线x=2 (B)直线x=-2
(C)y轴 (D)x轴
4、将抛物线 向左平移3个单位所得的抛物线的函数关系式为( )
A、 B、
C、 D、
5、抛物线 是由抛物线 向 平移 个单位得到的,平称后的抛物线对称轴是 ,顶点坐标是 ,当x= 时,y有最 值,其值是 。
A
D
y=-X2
右
1
直线x=1
(1,0)
1
大
0
6、抛物线y=4(x-3)2的开口方向 ,对称轴是 ,顶点坐标是 ,抛物线是最 点,
当x= 时,y有最 值,其值为 。
抛物线与x轴交点坐标 ,与y轴交点坐标 。
向上
直线x=3
(3,0)
低
3
小
0
(3,0)
(0,36)
7、求形状与y=-2(x+3)2的图象形状相同,但开口方向不同,顶点坐标是(1,0)的抛物线解析式。
小结 拓展
你认为今天这节课最需要掌握的是 ________________ ?
