沪科版九年级上册数学 21.2.5二次函数y=ax^2+bx+c的图像和性质 课件(共16张PPT)
文档属性
| 名称 | 沪科版九年级上册数学 21.2.5二次函数y=ax^2+bx+c的图像和性质 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-08 19:42:41 | ||
图片预览




文档简介
(共16张PPT)
y=ax2+bx+c的图象与性质
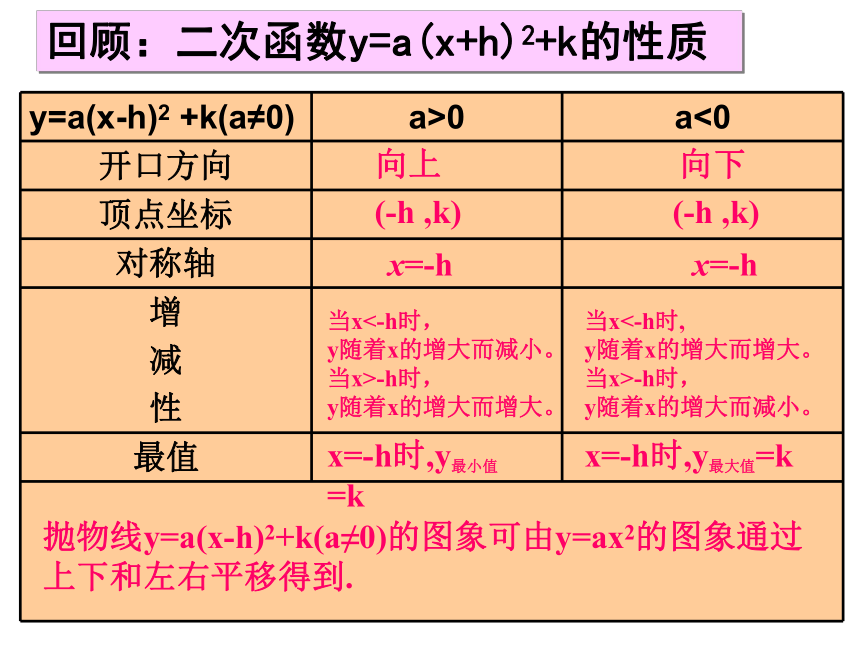
回顾:二次函数y=a(x+h)2+k的性质
y=a(x-h)2 +k(a≠0) a>0 a<0
开口方向
顶点坐标
对称轴
增
减
性
最值
向上
向下
(-h ,k)
(-h ,k)
x=-h
x=-h
当x<-h时,
y随着x的增大而减小。
当x>-h时,
y随着x的增大而增大。
当x<-h时,
y随着x的增大而增大。
当x>-h时,
y随着x的增大而减小。
x=-h时,y最小值=k
x=-h时,y最大值=k
抛物线y=a(x-h)2+k(a≠0)的图象可由y=ax2的图象通过上下和左右平移得到.
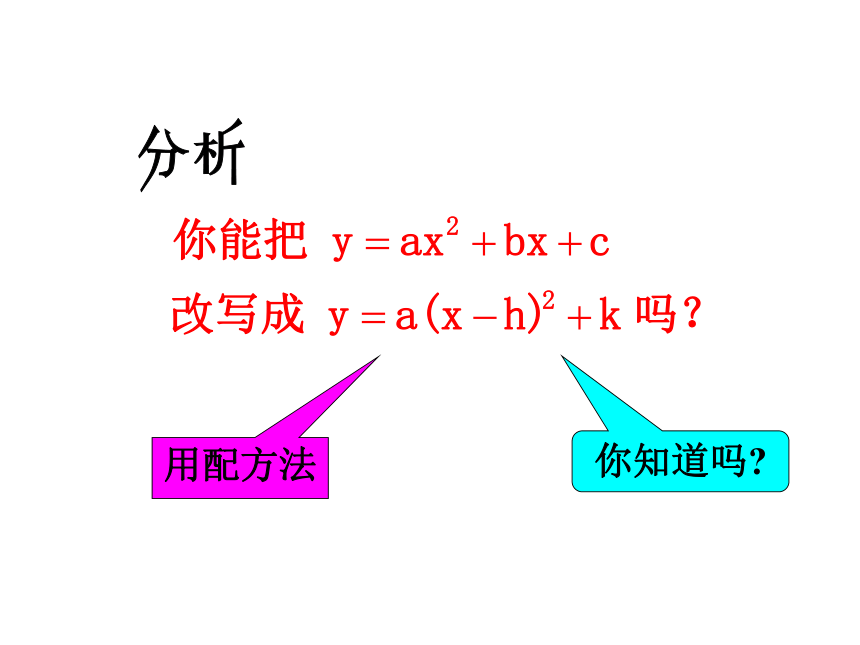
用配方法
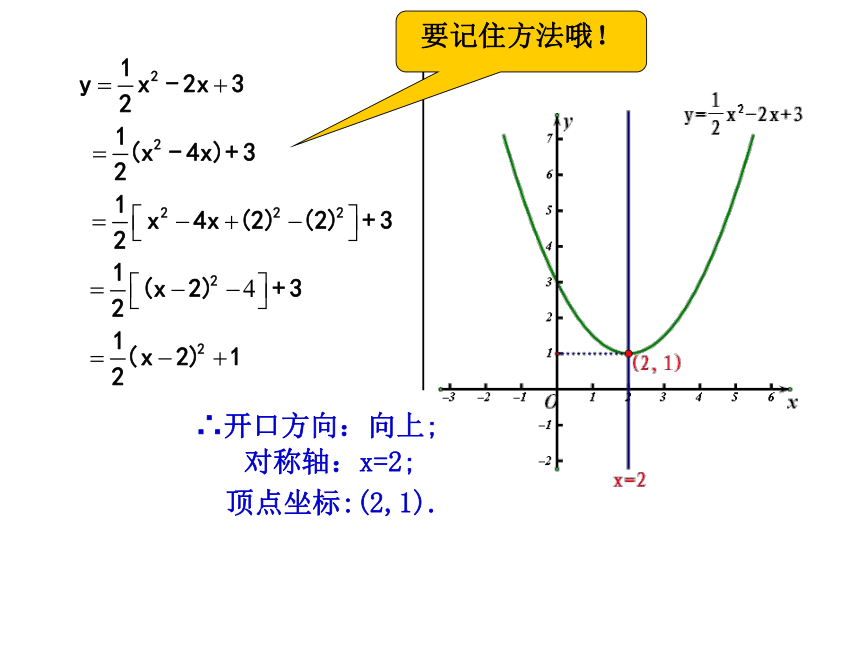
∴开口方向:向上;
对称轴:x=2;
顶点坐标:(2,1).
要记住方法哦!
∴开口方向:向上;
对称轴:x=2;
顶点坐标:(2,1).
∴开口方向:向上;
对称轴:x=2;
顶点坐标:(2,1).
你知道吗
用配方法
∴开口方向:由a决定;
要记住公式哦!
回顾:二次函数y=ax2+bx+c的性质
y=ax2 +bx+c
(a≠0) a>0 a<0
开口方向
顶点坐标
对称轴
增
减
性
最值
向上
向下
在对称轴的左侧,
y随着x的增大而减小。
在对称轴的右侧,
y随着x的增大而增大。
在对称轴的左侧,
y随着x的增大而增大。
在对称轴的右侧,
y随着x的增大而减小。
x= -
b
2a
x= -
b
2a
y最小值=
4ac-b2
4a
x= -
b
2a
(- , )
b
2a
4ac-b2
4a
(- , )
b
2a
4ac-b2
4a
y最大值=
4ac-b2
4a
x= -
b
2a
1.抛物线y=x2-4x+3与y轴的交点坐标是 ,
与x轴的交点坐标是 。
(0,3)
(1,0)或(3,0)
抛物线与y轴的交点有什么特征?
抛物线与x轴的交点有什么特征?
最 值,最 值 y= 。
4.函数y=4x2-3x-1,当x= 时,函数值y取得
5.抛物线y=x2-5x+6与y轴的交点坐标是 ,与x轴的交点坐标是 。
1.把二次函数y=-5(x- )2+ 写成y=ax2+bx+c的形式,
1
2
1
4
则a= b= c= 。
3.抛物线y=- x2-x+ 的顶点坐标是 ,
1
2
5
2
对称轴是 。
2.抛物线y=2x2-4x-5化成y=a(x-h)2+k的形式为
5
-5
-1
y=2(x-1)2-7
(-1,3)
x=-1
(0,6)
(2,0)或(3,0)
3
8
小
小
25
16
y=ax2+bx+c的图象与性质
回顾:二次函数y=a(x+h)2+k的性质
y=a(x-h)2 +k(a≠0) a>0 a<0
开口方向
顶点坐标
对称轴
增
减
性
最值
向上
向下
(-h ,k)
(-h ,k)
x=-h
x=-h
当x<-h时,
y随着x的增大而减小。
当x>-h时,
y随着x的增大而增大。
当x<-h时,
y随着x的增大而增大。
当x>-h时,
y随着x的增大而减小。
x=-h时,y最小值=k
x=-h时,y最大值=k
抛物线y=a(x-h)2+k(a≠0)的图象可由y=ax2的图象通过上下和左右平移得到.
用配方法
∴开口方向:向上;
对称轴:x=2;
顶点坐标:(2,1).
要记住方法哦!
∴开口方向:向上;
对称轴:x=2;
顶点坐标:(2,1).
∴开口方向:向上;
对称轴:x=2;
顶点坐标:(2,1).
你知道吗
用配方法
∴开口方向:由a决定;
要记住公式哦!
回顾:二次函数y=ax2+bx+c的性质
y=ax2 +bx+c
(a≠0) a>0 a<0
开口方向
顶点坐标
对称轴
增
减
性
最值
向上
向下
在对称轴的左侧,
y随着x的增大而减小。
在对称轴的右侧,
y随着x的增大而增大。
在对称轴的左侧,
y随着x的增大而增大。
在对称轴的右侧,
y随着x的增大而减小。
x= -
b
2a
x= -
b
2a
y最小值=
4ac-b2
4a
x= -
b
2a
(- , )
b
2a
4ac-b2
4a
(- , )
b
2a
4ac-b2
4a
y最大值=
4ac-b2
4a
x= -
b
2a
1.抛物线y=x2-4x+3与y轴的交点坐标是 ,
与x轴的交点坐标是 。
(0,3)
(1,0)或(3,0)
抛物线与y轴的交点有什么特征?
抛物线与x轴的交点有什么特征?
最 值,最 值 y= 。
4.函数y=4x2-3x-1,当x= 时,函数值y取得
5.抛物线y=x2-5x+6与y轴的交点坐标是 ,与x轴的交点坐标是 。
1.把二次函数y=-5(x- )2+ 写成y=ax2+bx+c的形式,
1
2
1
4
则a= b= c= 。
3.抛物线y=- x2-x+ 的顶点坐标是 ,
1
2
5
2
对称轴是 。
2.抛物线y=2x2-4x-5化成y=a(x-h)2+k的形式为
5
-5
-1
y=2(x-1)2-7
(-1,3)
x=-1
(0,6)
(2,0)或(3,0)
3
8
小
小
25
16
