沪科版九年级上册数学 21.4.2求最值问题 课件(共20张PPT)
文档属性
| 名称 | 沪科版九年级上册数学 21.4.2求最值问题 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-08 19:39:07 | ||
图片预览



文档简介
(共20张PPT)
1 2 3 4 5
0
y
1
2
-1
x
-1
0
x
y
姚明,1980年9月12日生于上海,是中国篮球的标志和骄傲,原中国国家篮球队队员,曾效力NBA的休斯顿火箭队。
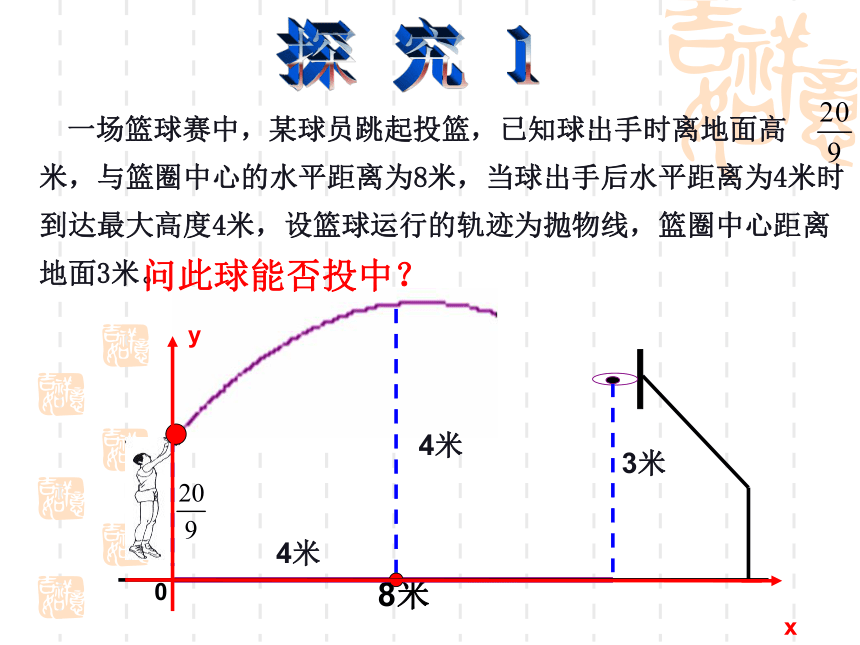
一场篮球赛中,某球员跳起投篮,已知球出手时离地面高 米,与篮圈中心的水平距离为8米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行的轨迹为抛物线,篮圈中心距离地面3米。
问此球能否投中?
3米
8米
4米
4米
0
x
y
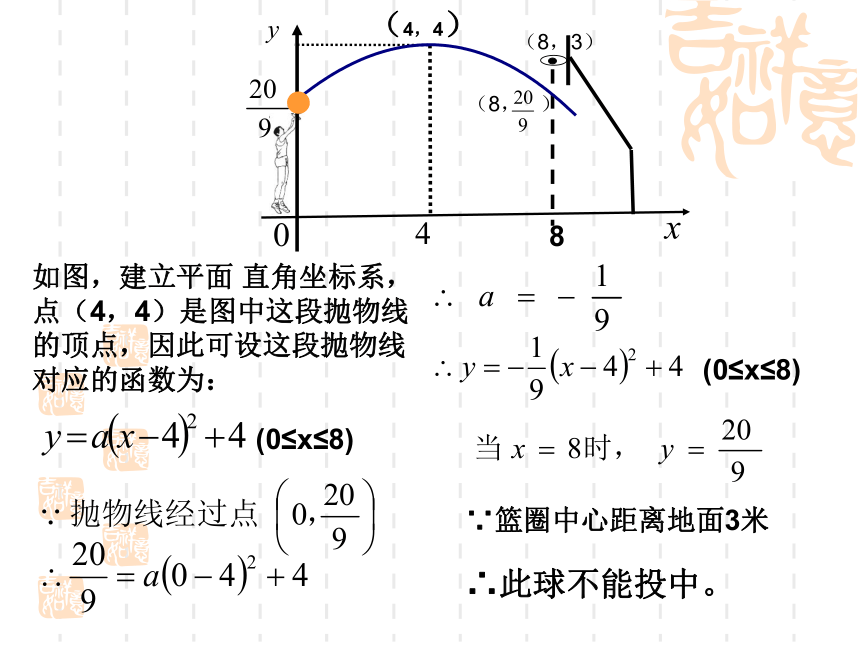
如图,建立平面 直角坐标系,点(4,4)是图中这段抛物线的顶点,因此可设这段抛物线对应的函数为:
(0≤x≤8)
(0≤x≤8)
∵篮圈中心距离地面3米
∴此球不能投中。
8
(4,4)
(8,3)
(8, )
假设出手的角度和力度都不变,则如何才能使此球命中
跳得高一点
向前平移一点
8
(4,4)
拓展与延伸
0
3
x
y
(8 , 3)
(1) 在出手角度和力度都不变的情况下,该球员的出手高度为多少时能将篮球投入篮圈
(0,3)
该球员的出手高度为
3m时能将篮球投入篮圈
0
3
x
(8,3)
(7,3)
(2) 在出手角度、力度及高度都不变的情况下,则该球员朝着篮球架再向前平移多少米后跳起投篮也能将篮球投入篮圈?
y
该球朝着篮球架再向前平移1m
后跳起投篮也能将篮球投入篮圈
跳台支柱
水面
A
B
(1)求该抛物线的解析式
某跳水运动员进行10m跳台跳水训练时,身体(看成一点)在空中的运动路线是如图所示坐标系下经过原点O的一条抛物线(图中标出的数据为已知条件)。在跳某个规定动作时,正常情况下,该运动员在空中的最高处距水面 m,到池边的距离为 m,同时,运动员在距水面高度为 5 m以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误。
基础知识之灵活运用
水面
跳台支柱
.
.
解:(1)由题意可知,顶点为
设抛物线的解析式为:
将原点(0,0)代入可得
则所求的抛物线解析式为:
A
B
水面
跳台支柱
.
解:(2)令 则
<5
∴此次跳水会出现失误
(2)在某次试跳中,测得运动员在空中的运动路线是①中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为 m,问此次跳水会不会出现失误?
A
B
2、教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为 (x-4)2+3,由此可知铅球推出的距离是( )m。
【解析】要求铅球推出的距离
实际是求当y=0时x的值。
1、 竖直向上发射的小球
的高度h(m)关于运动时间t(s)的函数
表达式为h=at2+bt,其图象如图所示. 若小
球在发射后第2秒与第6秒的高度相等,则
下列时刻中小球的高度最高的是( ).
A、第3秒 B、第3.5秒 C、第4秒 D、第6.5秒
10
C
操练场
6
2
h/m
t/s
O
4
实际问题
数学问题
(二次函数的问题)
转化
建立适当的坐标系
实际问题
的答案
检验
目标
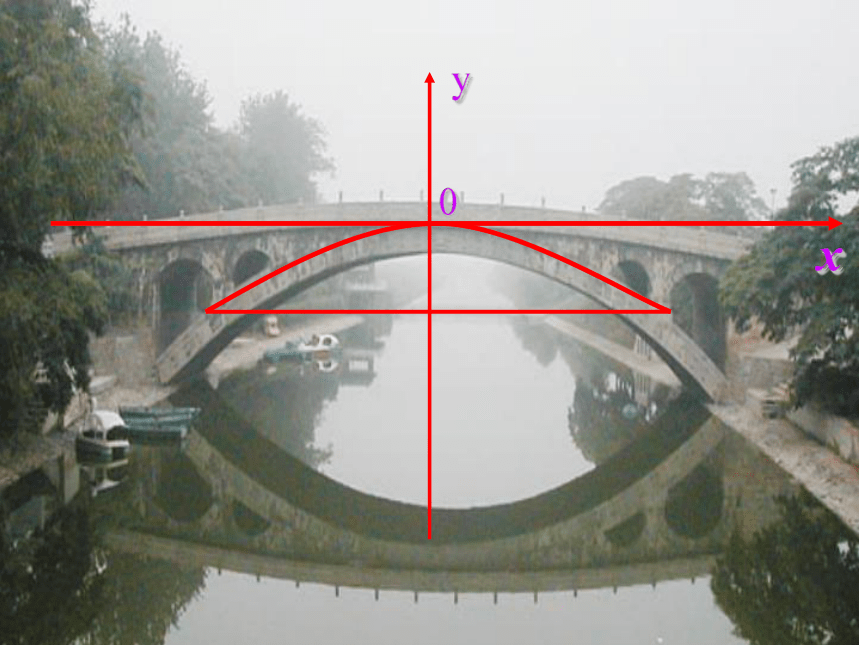
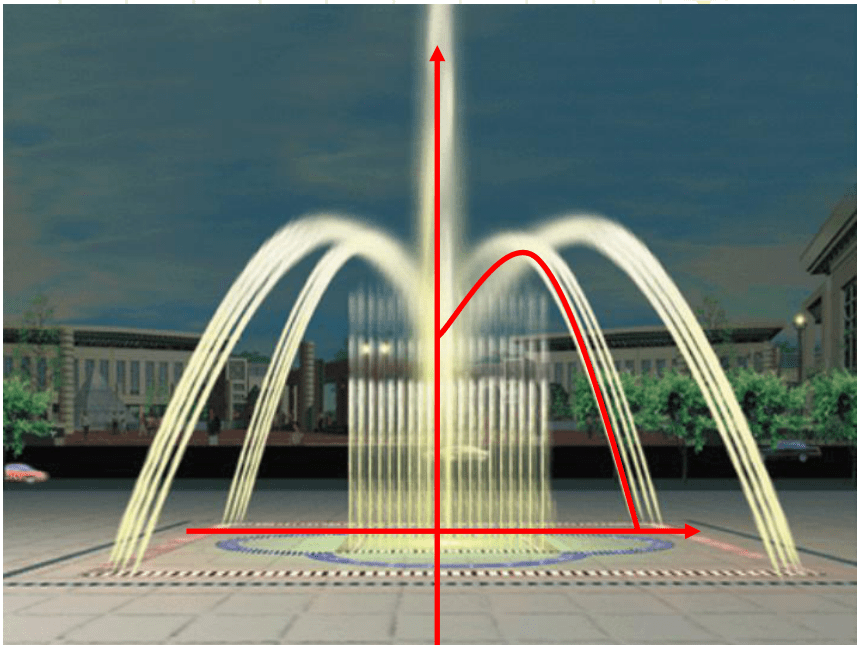
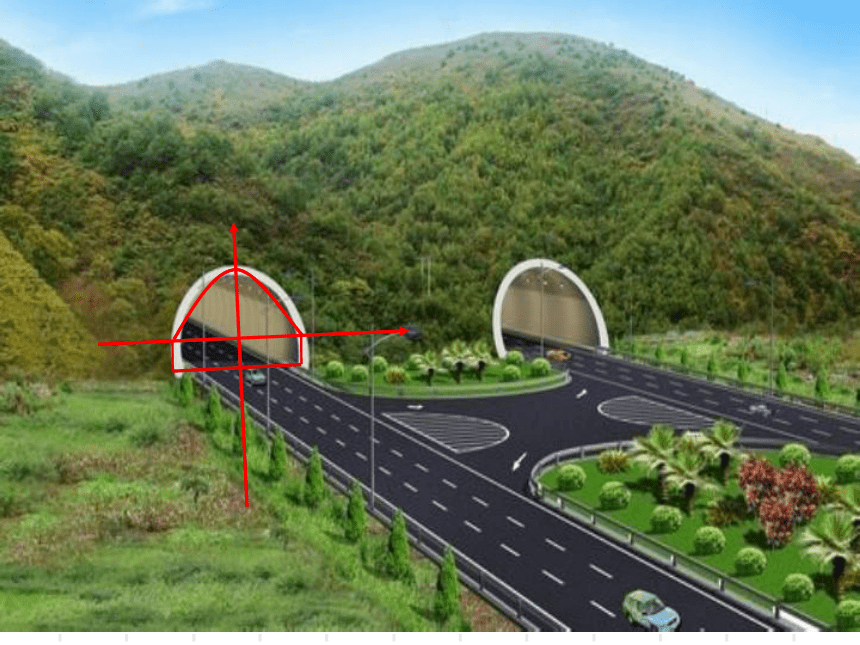
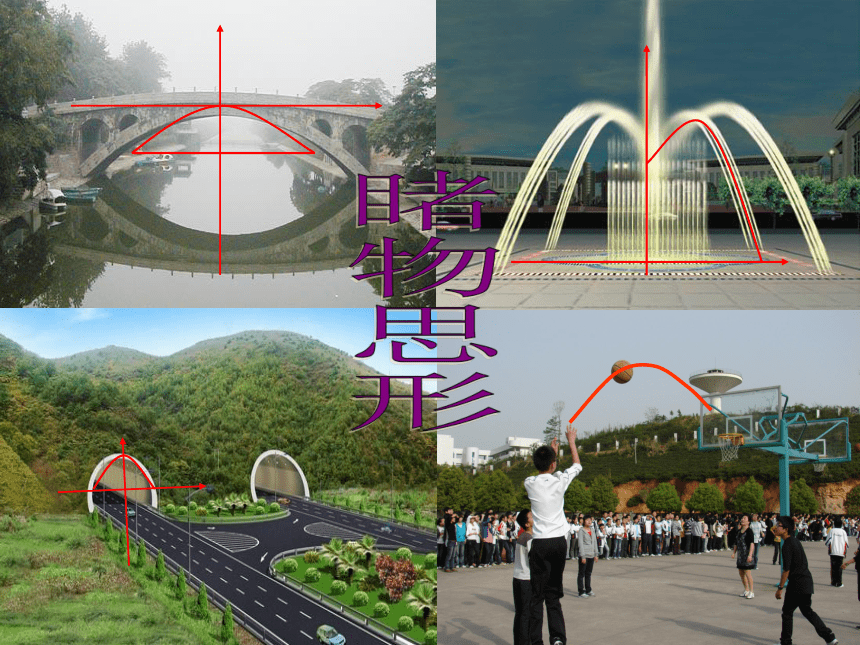
(有关抛物线形的实 际问题)
数学问题
的答案
利用二次函数的图象
求解
和性质
1、本节课你印象最深的是什么?
2、通过本节课的学习,你认为自己还有哪些方面还需要提高?
选做题:如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
(1)当h=2.6时,求y与x的关系式
(不要求写出自变量x的取值范围)
(2)当h=2.6时球能否越过球网?
球会不会出界? 请说明理由;
(3)若球一定能越过球网,又不
出边界,求h的取值范围。
图
1 2 3 4 5
0
y
1
2
-1
x
-1
0
x
y
姚明,1980年9月12日生于上海,是中国篮球的标志和骄傲,原中国国家篮球队队员,曾效力NBA的休斯顿火箭队。
一场篮球赛中,某球员跳起投篮,已知球出手时离地面高 米,与篮圈中心的水平距离为8米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行的轨迹为抛物线,篮圈中心距离地面3米。
问此球能否投中?
3米
8米
4米
4米
0
x
y
如图,建立平面 直角坐标系,点(4,4)是图中这段抛物线的顶点,因此可设这段抛物线对应的函数为:
(0≤x≤8)
(0≤x≤8)
∵篮圈中心距离地面3米
∴此球不能投中。
8
(4,4)
(8,3)
(8, )
假设出手的角度和力度都不变,则如何才能使此球命中
跳得高一点
向前平移一点
8
(4,4)
拓展与延伸
0
3
x
y
(8 , 3)
(1) 在出手角度和力度都不变的情况下,该球员的出手高度为多少时能将篮球投入篮圈
(0,3)
该球员的出手高度为
3m时能将篮球投入篮圈
0
3
x
(8,3)
(7,3)
(2) 在出手角度、力度及高度都不变的情况下,则该球员朝着篮球架再向前平移多少米后跳起投篮也能将篮球投入篮圈?
y
该球朝着篮球架再向前平移1m
后跳起投篮也能将篮球投入篮圈
跳台支柱
水面
A
B
(1)求该抛物线的解析式
某跳水运动员进行10m跳台跳水训练时,身体(看成一点)在空中的运动路线是如图所示坐标系下经过原点O的一条抛物线(图中标出的数据为已知条件)。在跳某个规定动作时,正常情况下,该运动员在空中的最高处距水面 m,到池边的距离为 m,同时,运动员在距水面高度为 5 m以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误。
基础知识之灵活运用
水面
跳台支柱
.
.
解:(1)由题意可知,顶点为
设抛物线的解析式为:
将原点(0,0)代入可得
则所求的抛物线解析式为:
A
B
水面
跳台支柱
.
解:(2)令 则
<5
∴此次跳水会出现失误
(2)在某次试跳中,测得运动员在空中的运动路线是①中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为 m,问此次跳水会不会出现失误?
A
B
2、教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为 (x-4)2+3,由此可知铅球推出的距离是( )m。
【解析】要求铅球推出的距离
实际是求当y=0时x的值。
1、 竖直向上发射的小球
的高度h(m)关于运动时间t(s)的函数
表达式为h=at2+bt,其图象如图所示. 若小
球在发射后第2秒与第6秒的高度相等,则
下列时刻中小球的高度最高的是( ).
A、第3秒 B、第3.5秒 C、第4秒 D、第6.5秒
10
C
操练场
6
2
h/m
t/s
O
4
实际问题
数学问题
(二次函数的问题)
转化
建立适当的坐标系
实际问题
的答案
检验
目标
(有关抛物线形的实 际问题)
数学问题
的答案
利用二次函数的图象
求解
和性质
1、本节课你印象最深的是什么?
2、通过本节课的学习,你认为自己还有哪些方面还需要提高?
选做题:如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
(1)当h=2.6时,求y与x的关系式
(不要求写出自变量x的取值范围)
(2)当h=2.6时球能否越过球网?
球会不会出界? 请说明理由;
(3)若球一定能越过球网,又不
出边界,求h的取值范围。
图
