2013-2014青岛版九年级上学期数学期末试题(含答案)
文档属性
| 名称 | 2013-2014青岛版九年级上学期数学期末试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 147.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-01-03 16:54:14 | ||
图片预览



文档简介
2013-2014学年度初三数学期末测试题(青岛版)
一、选择题(每小题只有一个正确的选项,每小题3分,共45分)
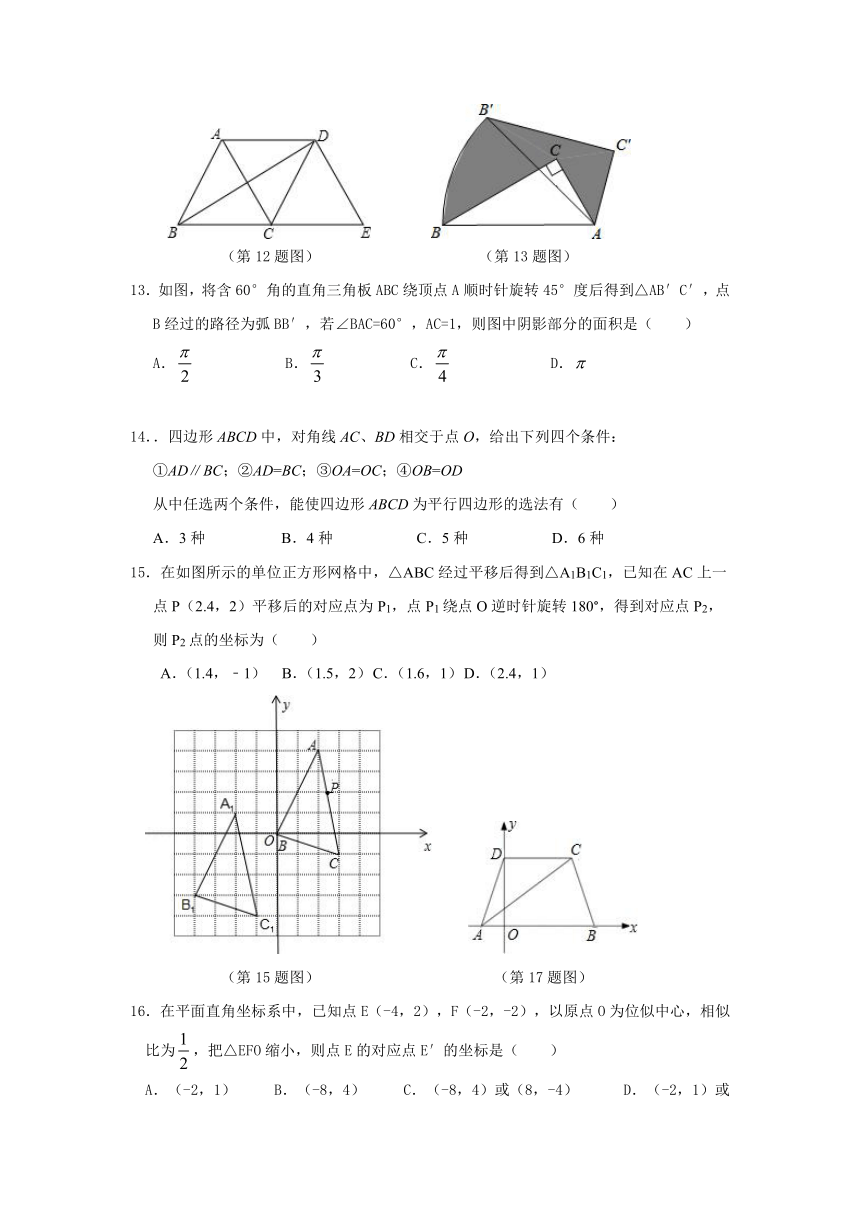
1.下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
2.方程x2-5x=0的解是( )
A.x1=0,x2=-5 B.x=5 C.x1=0,x2=5 D.x=0
3.一元二次方程(x+6)2=16可转化为两个一元一次方程,其中一个一元一次方程是x+6=4,则另一个一元一次方程是( )
A.x-6=-4 B.x-6=4 C.x+6=4 D.x+6=-4
4.顺次连接等腰梯形四边中点所得的四边形一定是( )
A.矩形 B.正方形 C.菱形 D.直角梯形
5.已知关于x的方程kx2+(1-k)x-1=0,下列说法正确的是( )
A.当k=0时,方程无解
B.当k=1时,方程有一个实数解
C.当k=-1时,方程有两个相等的实数解
D.当k≠0时,方程总有两个不相等的实数解.
6.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
A.AD=AB B.∠BOC=2∠D C.∠D+∠BOC=90° D.∠D=∠B
(第6题图) (第7题图)
7.如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )
A. 30° B. 35° C. 40° D. 50°
8.在梯形ABCD中,AD∥BC,对角线AC和BD交于点O,下列条件中,能判断梯形ABCD是等腰梯形的是( )
A.∠BDC=∠BCD B.∠ABC=∠DAB C.∠ADB=∠DAC D.∠AOB=∠BOC
9.如图,在□ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE、CF.则四边形AECF是( )
A.梯形 B.矩形 C.菱形 D.正方形
(第8题图) (第9题图) (第11题图)
10.两圆的半径分别为3和5,圆心距为7,则两圆的位置关系是( )
A.内切 B.相交 C.外切 D.外离
11.如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC= ∠BOD,则⊙O的半径为( )
A.4 B.5 C.4 D.3
12.如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:
①AD=BC;②BD、AC互相平分;③四边形ACED是菱形.
其中正确的个数是( )
A.0 B.1 C.2 D.3
(第12题图) (第13题图)
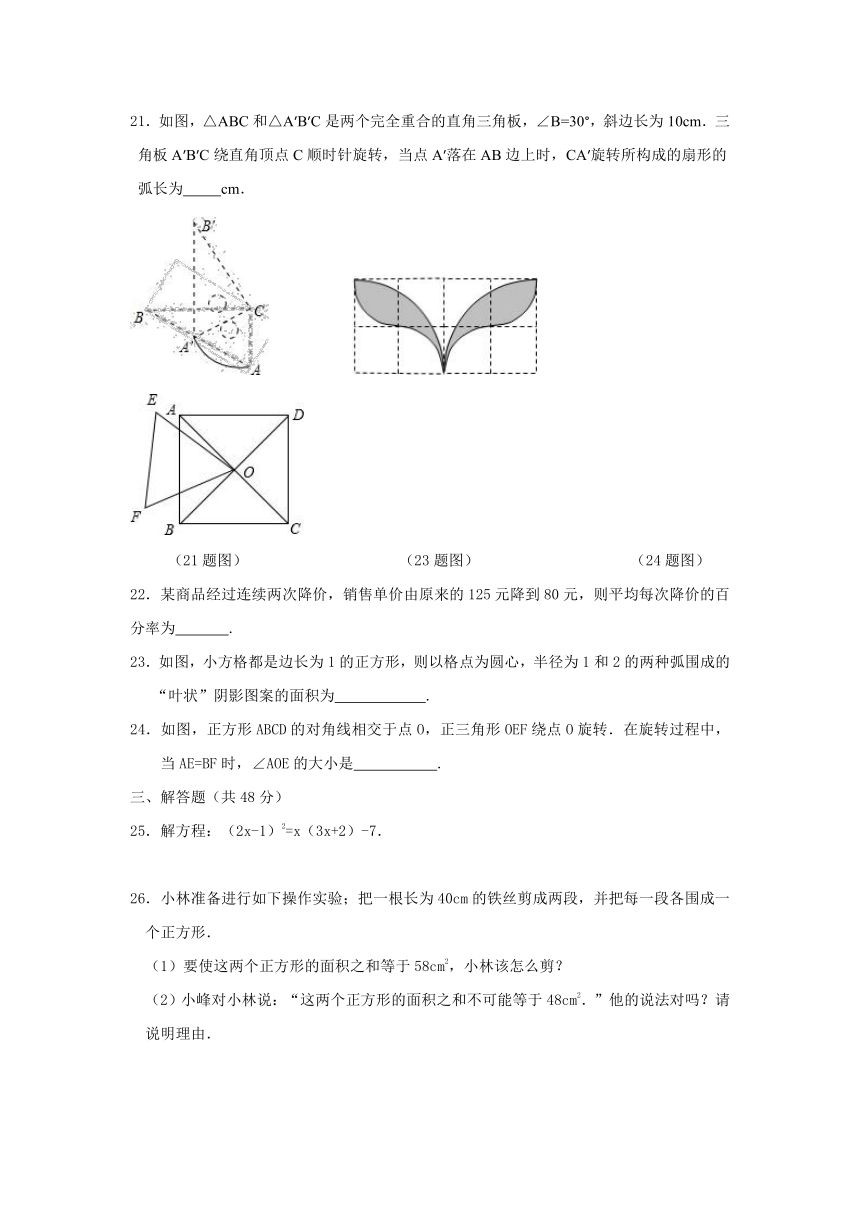
13.如图,将含60°角的直角三角板ABC绕顶点A顺时针旋转45°度后得到△AB′C′,点B经过的路径为弧BB′,若∠BAC=60°,AC=1,则图中阴影部分的面积是( )
A. B. C. D.
14..四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:
①AD∥BC;②AD=BC;③OA=OC;④OB=OD
从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
15.在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为( )
A.(1.4,﹣1) B.(1.5,2) C.(1.6,1) D.(2.4,1)
(第15题图) (第17题图)
16.在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为,把△EFO缩小,则点E的对应点E′的坐标是( )
A.(-2,1) B.(-8,4) C.(-8,4)或(8,-4) D.(-2,1)或(2,-1)
17.如图,在平面直角坐标中,等腰梯形ABCD的下底在x轴上,且B点坐标为(4,0),D点坐标为(0,3),则AC长为( )
A.4 B.5 C.6 D.不能确定
18.我们知道,一元二次方程没有实数根,即不存在一个实数的平方等于.
若我们规定一个新数“”,使其满足(即方程有一个根为)。并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有,从而对于任意正整数,我们可以得到, 同理可得 , , .那么的值为( ) A. 0 B. C. D.
19.如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则GH=( )
A. B. C. D.
(第19题图) (第20题图)
20.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为( )
A. B. C. D.
二、填空题(每小题3分,共12分)
21.如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为10cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,CA′旋转所构成的扇形的弧长为 cm.
(21题图) (23题图) (24题图)
22.某商品经过连续两次降价,销售单价由原来的125元降到80元,则平均每次降价的百分率为 .
23.如图,小方格都是边长为1的正方形,则以格点为圆心,半径为1和2的两种弧围成的“叶状”阴影图案的面积为 .
24.如图,正方形ABCD的对角线相交于点O,正三角形OEF绕点O旋转.在旋转过程中,当AE=BF时,∠AOE的大小是 .
三、解答题(共48分)
25.解方程:(2x-1)2=x(3x+2)-7.
26.小林准备进行如下操作实验;把一根长为40cm的铁丝剪成两段,并把每一段各围成一个正方形.
(1)要使这两个正方形的面积之和等于58cm2,小林该怎么剪?
(2)小峰对小林说:“这两个正方形的面积之和不可能等于48cm2.”他的说法对吗?请说明理由.
27.某商店准备购进甲、乙两种商品.已知甲商品每件进价15元,售价20元;乙商品每件进价35元,售价45元.
(1)若该商店同时购进甲、乙两种商品共100件,恰好用去2700元,求购进甲、乙两种商品各多少件?
(2)若该商店准备用不超过3100元购进甲、乙两种商品共100件,且这两种商品全部售出后获利不少于890元,问应该怎样进货,才能使总利润最大,最大利润是多少?(利润=售价-进价)
28.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
29.如图,已知⊙O是等腰直角三角形ADE的外接圆,∠ADE=90°,延长ED到C使DC=AD,以AD,DC为邻边作正方形ABCD,连接AC,连接BE交AC于点H.求证:
(1)AC是⊙O的切线.
(2)HC=2AH.
参考答案
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
B C D C C B A C C B B D A B C D B D B A
21.; 22.20% ; 23.2π-4; 24.15°或165°;
25.解:(2x-1)2=x(3x+2)-7,
4x2-4x+1=3x2+2x-7,
x2-6x=-8,
(x-3)2=1,
x-3=±1,
x1=2,x2=4.
26. 解:(1)设剪成的较短的这段为xcm,较长的这段就为(40-x)cm,由题意,得
()2+()2=58,
解得:x1=12,x2=28,
当x=12时,较长的为40-12=28cm,
当x=28时,较长的为40-28=12<28(舍去)
∴较短的这段为12cm,较长的这段就为28cm;
(2)设剪成的较短的这段为mcm,较长的这段就为(40-m)cm,由题意,得
()2+()2=48,
变形为:m2-40m+416=0,
∵△=(-40)2-4×416=-64<0,
∴原方程无解,
∴小峰的说法正确,这两个正方形的面积之和不可能等于48cm2.
27. 解:(1)设购进甲种商品x件,购进乙商品y件,
根据题意得:,
解得:,
答:商店购进甲种商品40件,购进乙种商品60件;
(2)设商店购进甲种商品a件,则购进乙种商品(100-a)件,
根据题意列得:,
解得:20≤a≤22,
∵总利润W=5a+10(100-a)=-5a+1000,W是关于a的一次函数,W随a的增大而减小,
∴当a=20时,W有最大值,此时W=900,且100-20=80,
答:应购进甲种商品20件,乙种商品80件,才能使总利润最大,最大利润为900元.
28. 解:(1)BD=CD.
理由如下:∵AF∥BC,
∴∠AFE=∠DCE,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEC中,,
∴△AEF≌△DEC(AAS),
∴AF=CD,
∵AF=BD,
∴BD=CD;
(2)当△ABC满足:AB=AC时,四边形AFBD是矩形.
理由如下:∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD,
∴∠ADB=90°,
∴□AFBD是矩形.
29. 证明:(1)∵∠ADE=90°,
∴AE为⊙O的直径,
∵△ADE为等腰直角三角形,
∴∠EAD=45°,
∵四边形ABCD为正方形,
∴∠DAC=45°,
∴∠EAC=45°+45°=90°,
∴AC⊥AE,
∴AC是⊙O的切线;
(2)∵四边形ABCD为正方形,
∴AB∥CD,
∴△ABH∽△CEH,
∴AH:CH=AB:ED,
∵△ADE为等腰直角三角形,
∴AD=ED,
而AD=AB=DC,
∴EC=2AB,
∴AH:CH=1:2,
即HC=2AH.
一、选择题(每小题只有一个正确的选项,每小题3分,共45分)
1.下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
2.方程x2-5x=0的解是( )
A.x1=0,x2=-5 B.x=5 C.x1=0,x2=5 D.x=0
3.一元二次方程(x+6)2=16可转化为两个一元一次方程,其中一个一元一次方程是x+6=4,则另一个一元一次方程是( )
A.x-6=-4 B.x-6=4 C.x+6=4 D.x+6=-4
4.顺次连接等腰梯形四边中点所得的四边形一定是( )
A.矩形 B.正方形 C.菱形 D.直角梯形
5.已知关于x的方程kx2+(1-k)x-1=0,下列说法正确的是( )
A.当k=0时,方程无解
B.当k=1时,方程有一个实数解
C.当k=-1时,方程有两个相等的实数解
D.当k≠0时,方程总有两个不相等的实数解.
6.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
A.AD=AB B.∠BOC=2∠D C.∠D+∠BOC=90° D.∠D=∠B
(第6题图) (第7题图)
7.如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )
A. 30° B. 35° C. 40° D. 50°
8.在梯形ABCD中,AD∥BC,对角线AC和BD交于点O,下列条件中,能判断梯形ABCD是等腰梯形的是( )
A.∠BDC=∠BCD B.∠ABC=∠DAB C.∠ADB=∠DAC D.∠AOB=∠BOC
9.如图,在□ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE、CF.则四边形AECF是( )
A.梯形 B.矩形 C.菱形 D.正方形
(第8题图) (第9题图) (第11题图)
10.两圆的半径分别为3和5,圆心距为7,则两圆的位置关系是( )
A.内切 B.相交 C.外切 D.外离
11.如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC= ∠BOD,则⊙O的半径为( )
A.4 B.5 C.4 D.3
12.如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:
①AD=BC;②BD、AC互相平分;③四边形ACED是菱形.
其中正确的个数是( )
A.0 B.1 C.2 D.3
(第12题图) (第13题图)
13.如图,将含60°角的直角三角板ABC绕顶点A顺时针旋转45°度后得到△AB′C′,点B经过的路径为弧BB′,若∠BAC=60°,AC=1,则图中阴影部分的面积是( )
A. B. C. D.
14..四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:
①AD∥BC;②AD=BC;③OA=OC;④OB=OD
从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
15.在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为( )
A.(1.4,﹣1) B.(1.5,2) C.(1.6,1) D.(2.4,1)
(第15题图) (第17题图)
16.在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为,把△EFO缩小,则点E的对应点E′的坐标是( )
A.(-2,1) B.(-8,4) C.(-8,4)或(8,-4) D.(-2,1)或(2,-1)
17.如图,在平面直角坐标中,等腰梯形ABCD的下底在x轴上,且B点坐标为(4,0),D点坐标为(0,3),则AC长为( )
A.4 B.5 C.6 D.不能确定
18.我们知道,一元二次方程没有实数根,即不存在一个实数的平方等于.
若我们规定一个新数“”,使其满足(即方程有一个根为)。并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有,从而对于任意正整数,我们可以得到, 同理可得 , , .那么的值为( ) A. 0 B. C. D.
19.如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则GH=( )
A. B. C. D.
(第19题图) (第20题图)
20.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为( )
A. B. C. D.
二、填空题(每小题3分,共12分)
21.如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为10cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,CA′旋转所构成的扇形的弧长为 cm.
(21题图) (23题图) (24题图)
22.某商品经过连续两次降价,销售单价由原来的125元降到80元,则平均每次降价的百分率为 .
23.如图,小方格都是边长为1的正方形,则以格点为圆心,半径为1和2的两种弧围成的“叶状”阴影图案的面积为 .
24.如图,正方形ABCD的对角线相交于点O,正三角形OEF绕点O旋转.在旋转过程中,当AE=BF时,∠AOE的大小是 .
三、解答题(共48分)
25.解方程:(2x-1)2=x(3x+2)-7.
26.小林准备进行如下操作实验;把一根长为40cm的铁丝剪成两段,并把每一段各围成一个正方形.
(1)要使这两个正方形的面积之和等于58cm2,小林该怎么剪?
(2)小峰对小林说:“这两个正方形的面积之和不可能等于48cm2.”他的说法对吗?请说明理由.
27.某商店准备购进甲、乙两种商品.已知甲商品每件进价15元,售价20元;乙商品每件进价35元,售价45元.
(1)若该商店同时购进甲、乙两种商品共100件,恰好用去2700元,求购进甲、乙两种商品各多少件?
(2)若该商店准备用不超过3100元购进甲、乙两种商品共100件,且这两种商品全部售出后获利不少于890元,问应该怎样进货,才能使总利润最大,最大利润是多少?(利润=售价-进价)
28.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
29.如图,已知⊙O是等腰直角三角形ADE的外接圆,∠ADE=90°,延长ED到C使DC=AD,以AD,DC为邻边作正方形ABCD,连接AC,连接BE交AC于点H.求证:
(1)AC是⊙O的切线.
(2)HC=2AH.
参考答案
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
B C D C C B A C C B B D A B C D B D B A
21.; 22.20% ; 23.2π-4; 24.15°或165°;
25.解:(2x-1)2=x(3x+2)-7,
4x2-4x+1=3x2+2x-7,
x2-6x=-8,
(x-3)2=1,
x-3=±1,
x1=2,x2=4.
26. 解:(1)设剪成的较短的这段为xcm,较长的这段就为(40-x)cm,由题意,得
()2+()2=58,
解得:x1=12,x2=28,
当x=12时,较长的为40-12=28cm,
当x=28时,较长的为40-28=12<28(舍去)
∴较短的这段为12cm,较长的这段就为28cm;
(2)设剪成的较短的这段为mcm,较长的这段就为(40-m)cm,由题意,得
()2+()2=48,
变形为:m2-40m+416=0,
∵△=(-40)2-4×416=-64<0,
∴原方程无解,
∴小峰的说法正确,这两个正方形的面积之和不可能等于48cm2.
27. 解:(1)设购进甲种商品x件,购进乙商品y件,
根据题意得:,
解得:,
答:商店购进甲种商品40件,购进乙种商品60件;
(2)设商店购进甲种商品a件,则购进乙种商品(100-a)件,
根据题意列得:,
解得:20≤a≤22,
∵总利润W=5a+10(100-a)=-5a+1000,W是关于a的一次函数,W随a的增大而减小,
∴当a=20时,W有最大值,此时W=900,且100-20=80,
答:应购进甲种商品20件,乙种商品80件,才能使总利润最大,最大利润为900元.
28. 解:(1)BD=CD.
理由如下:∵AF∥BC,
∴∠AFE=∠DCE,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEC中,,
∴△AEF≌△DEC(AAS),
∴AF=CD,
∵AF=BD,
∴BD=CD;
(2)当△ABC满足:AB=AC时,四边形AFBD是矩形.
理由如下:∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD,
∴∠ADB=90°,
∴□AFBD是矩形.
29. 证明:(1)∵∠ADE=90°,
∴AE为⊙O的直径,
∵△ADE为等腰直角三角形,
∴∠EAD=45°,
∵四边形ABCD为正方形,
∴∠DAC=45°,
∴∠EAC=45°+45°=90°,
∴AC⊥AE,
∴AC是⊙O的切线;
(2)∵四边形ABCD为正方形,
∴AB∥CD,
∴△ABH∽△CEH,
∴AH:CH=AB:ED,
∵△ADE为等腰直角三角形,
∴AD=ED,
而AD=AB=DC,
∴EC=2AB,
∴AH:CH=1:2,
即HC=2AH.
同课章节目录
