4.2.2等差数列的前n项和 课件(共24张PPT)
文档属性
| 名称 | 4.2.2等差数列的前n项和 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-09 13:28:35 | ||
图片预览




文档简介
(共24张PPT)
等差数列的前n项和
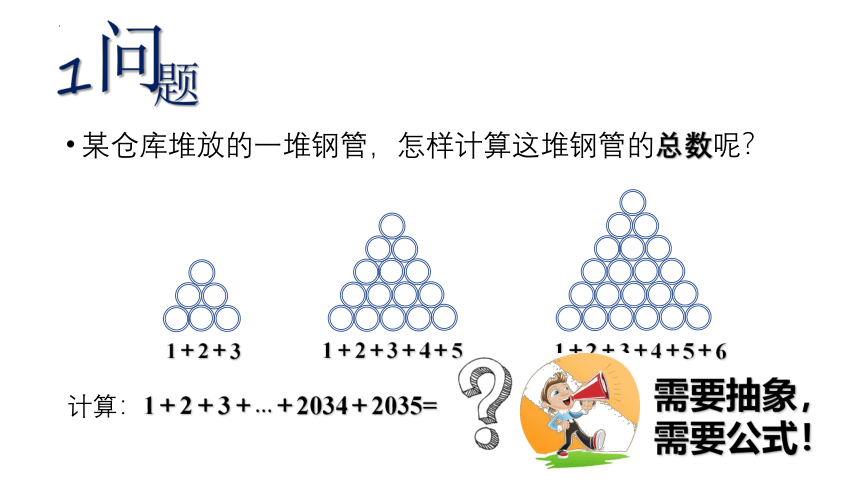
某仓库堆放的一堆钢管,怎样计算这堆钢管的总数呢?
1+2+3
1+2+3+4+5
1+2+3+4+5+6
计算:1+2+3+…+2034+2035=
问
题
1
需要抽象,
需要公式!
已知{an}是等差数列,求数列{an}的前n项和
Sn=a1+a2+…+an.
运算角度:
想找到一个没有…且关于n的简单的代数式!
问
题
1
记为Sn
问题:求前n个正整数的和:
就是毕达哥拉斯学派提出的“三角形数”.
如何求呢?
毕达哥拉斯(Pythagoras)
约公元前580年—约前500年
古希腊数学家、哲学家
f(1)=1
f(2) =3
f(3) =6
f(4) =10
f(5) =15
问
题
1
问题:求前n个正整数的和: f(n) =1+2+…+n.
目标:将f(n)写成关于n的简单表达式.
sss
ttt
ggg
iii
数学是自己思考的产物。首先要能够思考起来,
用自己的见解和别人的见解交换,会有很好地效果。
——陈省身
探
究
2
已知{an}是等差数列,求数列{an}的前n项和
Sn=a1+a2+…+an.
运算角度:
归
纳
3
f (n-1)
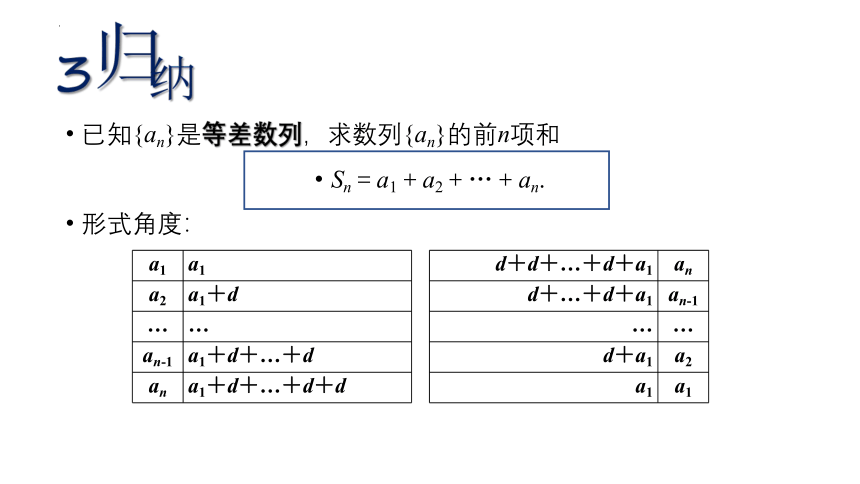
已知{an}是等差数列,求数列{an}的前n项和
Sn=a1+a2+…+an.
形式角度:
a1 a1
a2 a1+d
… …
an-1 a1+d+…+d
an a1+d+…+d+d
d+d+…+d+a1 an
d+…+d+a1 an-1
… …
d+a1 a2
a1 a1
归
纳
3
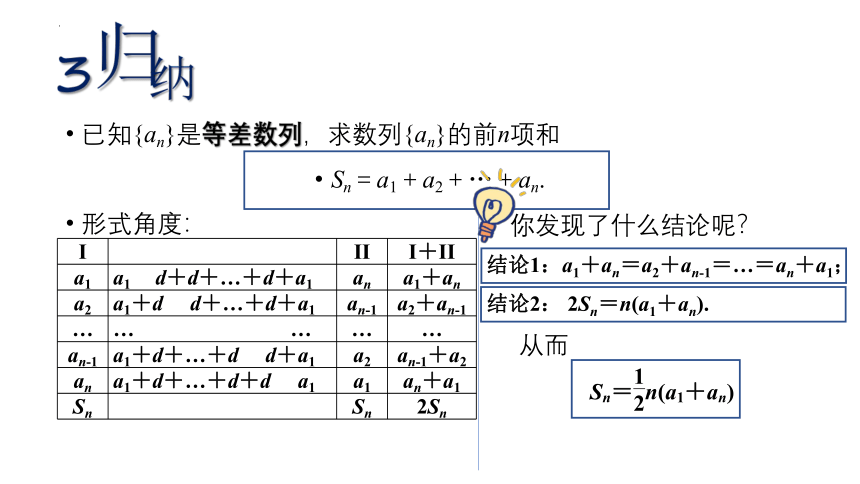
已知{an}是等差数列,求数列{an}的前n项和
Sn=a1+a2+…+an.
形式角度:
结论1:a1+an=a2+an-1=…=an+a1;
结论2: 2Sn=n(a1+an).
I II I+II
a1 a1 d+d+…+d+a1 an a1+an
a2 a1+d d+…+d+a1 an-1 a2+an-1
… … … … …
an-1 a1+d+…+d d+a1 a2 an-1+a2
an a1+d+…+d+d a1 a1 an+a1
Sn Sn 2Sn
你发现了什么结论呢?
从而
归
纳
3
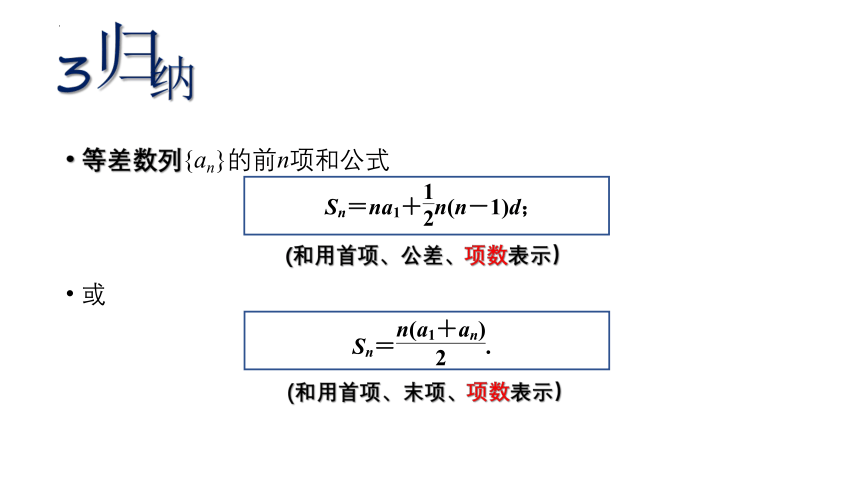
等差数列{an}的前n项和公式
或
(和用首项、公差、项数表示)
(和用首项、末项、项数表示)
归
纳
3
应
用
4
(和=均值×项数)
应
用
4
和式是宽度为1的矩形面积之和.
n 1 2 3 4 5 6 7 8 9 10
an 3 3.5 4 4.5 5 5.5 6 6.5 7 7.5
能否联想到物理学中某种表示?
应
用
4
例2.在等差数列中,完成如下问题:
(1)第1项到第3项的和为3,第4项到第6项的和为6,求第7项到第9项的和;
(2)第1项到第5项的和为5,第6项到第10项的和为10,求第11项到第15项的和;
(3)第1项到第4项的和为4,第5项到第8项的和为8,求第9项到第12项的和.
9
15
12
你能发现什么呢?
应
用
4
猜想:已知{an}是公差为d的等差数列,Sn是其前n项和,则
Sn,S2n-Sn,S3n-S2n,…
成等差数列.
探索:在等差数列{an}中
a1+a2+…+an,an+1+an+2+…+a2n,a2n+1+a2n+2+…+a3n,…
成等差数列.
成首项是 ,公差是 的等差数列.
Sn
n2 d
应
用
4
发现问题
提出问题
分析问题
解决问题
升
华
5
问题
探究
抽象
化归
建模
归纳猜想
倒序相加
应用
优化计算
数据意识
二次建模
升
华
5
杨辉在《详解九章算法》(1261)提出“三角垛”:
下广一面十二个,上尖. 问:计几何?
术文说:下广加一乘之. 下广加二,乘之,立高方积,如六而一.
答数:364.
思考:你能用今天的研究方法加以研究吗?
杨辉,字谦光,汉族,
南宋杰出的数学家
升
华
5
若n为偶数,则
f(n) =1+2+… +(n-1)+n
=(1+n) +(2 +(n-1)) + …
=
分组配对
若n为奇数,则
f(n) = f(n-1) +n
=
=
几何直观
n+1列
n行
归纳猜想
f(1)=1, f(2) =3, f(3) =6, f(4) =10, f(5) =15,…
猜测: f(n)=An2+Bn+C,
解得:
n 1 2 3 4 5
f(n) 1 3 6 10 15
猜想正确吗?
裂项相消
22-12=3,
32-22=5,
…
(n+1)2-n2=2n+1,
将这n个等式的左、右分别相加,得
(n+1)2-12=(2×1+1)+(2×2+1)+…+(2n+1),
即
2(1+2+…+n)+n=n(n+2),
裂项相消
数学有两个侧面,一方面它是欧几里得式严谨的科学,从这方面看数学像是一门系统的演绎科学;但另一方面,创造过程中的数学看起来却像一门实验性的归纳科学.
——G·波利亚
George Polya(1887-1985)
美籍匈牙利数学家。
Thanks!
等差数列的前n项和
某仓库堆放的一堆钢管,怎样计算这堆钢管的总数呢?
1+2+3
1+2+3+4+5
1+2+3+4+5+6
计算:1+2+3+…+2034+2035=
问
题
1
需要抽象,
需要公式!
已知{an}是等差数列,求数列{an}的前n项和
Sn=a1+a2+…+an.
运算角度:
想找到一个没有…且关于n的简单的代数式!
问
题
1
记为Sn
问题:求前n个正整数的和:
就是毕达哥拉斯学派提出的“三角形数”.
如何求呢?
毕达哥拉斯(Pythagoras)
约公元前580年—约前500年
古希腊数学家、哲学家
f(1)=1
f(2) =3
f(3) =6
f(4) =10
f(5) =15
问
题
1
问题:求前n个正整数的和: f(n) =1+2+…+n.
目标:将f(n)写成关于n的简单表达式.
sss
ttt
ggg
iii
数学是自己思考的产物。首先要能够思考起来,
用自己的见解和别人的见解交换,会有很好地效果。
——陈省身
探
究
2
已知{an}是等差数列,求数列{an}的前n项和
Sn=a1+a2+…+an.
运算角度:
归
纳
3
f (n-1)
已知{an}是等差数列,求数列{an}的前n项和
Sn=a1+a2+…+an.
形式角度:
a1 a1
a2 a1+d
… …
an-1 a1+d+…+d
an a1+d+…+d+d
d+d+…+d+a1 an
d+…+d+a1 an-1
… …
d+a1 a2
a1 a1
归
纳
3
已知{an}是等差数列,求数列{an}的前n项和
Sn=a1+a2+…+an.
形式角度:
结论1:a1+an=a2+an-1=…=an+a1;
结论2: 2Sn=n(a1+an).
I II I+II
a1 a1 d+d+…+d+a1 an a1+an
a2 a1+d d+…+d+a1 an-1 a2+an-1
… … … … …
an-1 a1+d+…+d d+a1 a2 an-1+a2
an a1+d+…+d+d a1 a1 an+a1
Sn Sn 2Sn
你发现了什么结论呢?
从而
归
纳
3
等差数列{an}的前n项和公式
或
(和用首项、公差、项数表示)
(和用首项、末项、项数表示)
归
纳
3
应
用
4
(和=均值×项数)
应
用
4
和式是宽度为1的矩形面积之和.
n 1 2 3 4 5 6 7 8 9 10
an 3 3.5 4 4.5 5 5.5 6 6.5 7 7.5
能否联想到物理学中某种表示?
应
用
4
例2.在等差数列中,完成如下问题:
(1)第1项到第3项的和为3,第4项到第6项的和为6,求第7项到第9项的和;
(2)第1项到第5项的和为5,第6项到第10项的和为10,求第11项到第15项的和;
(3)第1项到第4项的和为4,第5项到第8项的和为8,求第9项到第12项的和.
9
15
12
你能发现什么呢?
应
用
4
猜想:已知{an}是公差为d的等差数列,Sn是其前n项和,则
Sn,S2n-Sn,S3n-S2n,…
成等差数列.
探索:在等差数列{an}中
a1+a2+…+an,an+1+an+2+…+a2n,a2n+1+a2n+2+…+a3n,…
成等差数列.
成首项是 ,公差是 的等差数列.
Sn
n2 d
应
用
4
发现问题
提出问题
分析问题
解决问题
升
华
5
问题
探究
抽象
化归
建模
归纳猜想
倒序相加
应用
优化计算
数据意识
二次建模
升
华
5
杨辉在《详解九章算法》(1261)提出“三角垛”:
下广一面十二个,上尖. 问:计几何?
术文说:下广加一乘之. 下广加二,乘之,立高方积,如六而一.
答数:364.
思考:你能用今天的研究方法加以研究吗?
杨辉,字谦光,汉族,
南宋杰出的数学家
升
华
5
若n为偶数,则
f(n) =1+2+… +(n-1)+n
=(1+n) +(2 +(n-1)) + …
=
分组配对
若n为奇数,则
f(n) = f(n-1) +n
=
=
几何直观
n+1列
n行
归纳猜想
f(1)=1, f(2) =3, f(3) =6, f(4) =10, f(5) =15,…
猜测: f(n)=An2+Bn+C,
解得:
n 1 2 3 4 5
f(n) 1 3 6 10 15
猜想正确吗?
裂项相消
22-12=3,
32-22=5,
…
(n+1)2-n2=2n+1,
将这n个等式的左、右分别相加,得
(n+1)2-12=(2×1+1)+(2×2+1)+…+(2n+1),
即
2(1+2+…+n)+n=n(n+2),
裂项相消
数学有两个侧面,一方面它是欧几里得式严谨的科学,从这方面看数学像是一门系统的演绎科学;但另一方面,创造过程中的数学看起来却像一门实验性的归纳科学.
——G·波利亚
George Polya(1887-1985)
美籍匈牙利数学家。
Thanks!
