4.3.2角的比较与运算
图片预览







文档简介
课件21张PPT。4.3 角(第3课时)
4.3.2 角的比较与运算(1)义务教育教科书 数学 七年级 上册课件说明 本节课主要学习角的比较,角的和差,角平分线.角的比较,角的和差,角平分线是本章重要的几何基础知识,也是后续学习图形与几何必备的知识基础.学习目标:
1. 理解角的大小、和差、角平分线的几何意义及数量关系,并会用文字语言、图形语言、符号语言进行综合描述.
2. 经历类比线段的长短、和差、中点学习角的大小、和差、角平分线等过程,体会类比思想.温故知新,引入课题1.角是怎样形成的图形?2.请同学们回忆一下,前面我们学习了线段的哪些内容?3. 如图,已知线段AB、CD,你有哪些办法比较它们的大小?温故知新,引入课题1.叠合法2.度量法 类比线段大小的比较,你认为该如何比较两个角的大小?试着画图来解决.观察思考,探究新知1.度量法∠ABC >∠DEFBCA70°30°2.叠合法观察思考,探究新知步骤:
1. 将两个角的顶点及一边重合,
2. 两个角的另一边落在重合一边的同侧,3.由两个角的另一边的位置确定两个角的
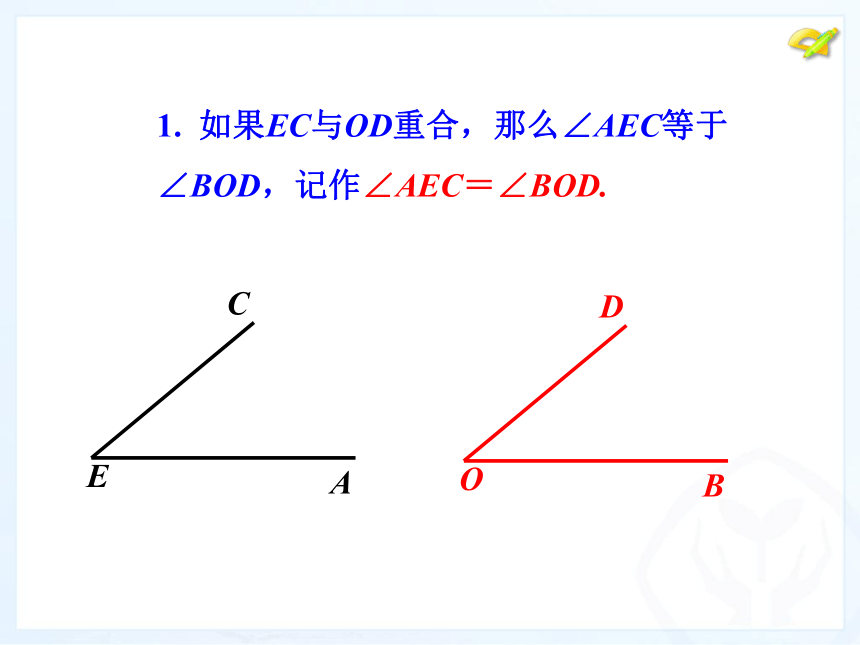
大小. 1. 如果EC与OD重合,那么∠AEC等于
∠BOD,记作∠AEC=∠BOD. 2.如果EC落在∠BOD的内部,那么∠AEC小
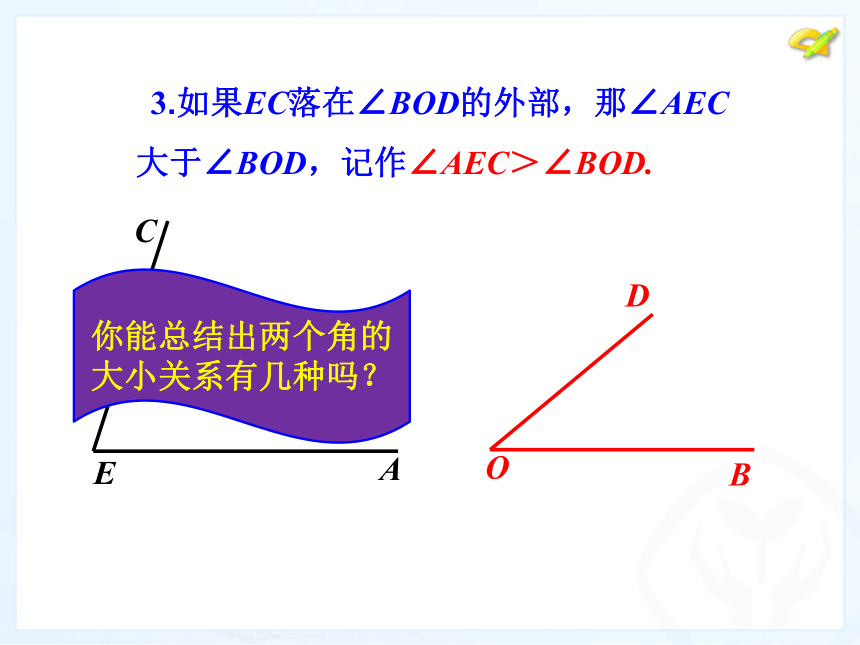
于∠BOD,记作∠AEC<∠BOD. 3.如果EC落在∠BOD的外部,那∠AEC
大于∠BOD,记作∠AEC>∠BOD.你能总结出两个角的大小关系有几种吗? 问题1
图中共有几个角?它们之间有什么关系?答:有三个角,关系是:∠BOC是 ∠AOC与 ∠AOB的差,记作 ∠BOC=∠AOC-∠AOB.∠AOC是∠AOB与 ∠BOC的和,记作 ∠AOC=∠AOB+∠BOC,∠AOB是 ∠AOC与 ∠BOC的差,记作 ∠AOB=∠AOC-∠BOC,观察思考,探究新知问题2
利用一副三角板,你能画出哪些度数的角?这些角有什么规律?观察思考,探究新知 问题3
如图,如果∠AOB=∠BOC,那么
∠AOC=2∠AOB=2 ,
∠AOB=∠BOC= .∠AOC∠BOC我们把射线OB叫做∠AOC的角平分线. 类比线段中点的定义,你能给角平分线下定义吗? 从一个角的顶点出发,把这个角分成相等的两个角的射线,叫这个角的平分线.观察思考,探究新知角的三等分线角的四等分线 问题4
如何作一个角的平分线?你能想到什么方法?度量法折纸法1.估计图中∠1与∠2的大小关系,
并用适当的方法验证.练习巩固,应用新知 适当改变角的位置,可以用叠合法检验.2.如图,∠AOB=90o,OC平分∠AOB,OE平分∠AOD,若∠EOC=60o,∠AOC= , ∠AOE= , ∠EOD= .
练习巩固,应用新知 45o15o15o练习巩固,应用新知 3.如图所示:
(1)∠AOC是哪两个角的和?
∠AOC=∠AOB+∠BOC.
(2)∠AOB是哪两个角的差?
∠AOB=∠AOC-∠BOC或∠AOD-∠BOD.
(3)如果∠AOB=∠COD,则∠AOC与∠BOD的大小关系如何?∠AOC=∠BOD.今天你学到了哪些知识?小结与回顾作业:
教科书习题4.3第4,5,6题.下节课我们继续学习!再见
4.3.2 角的比较与运算(1)义务教育教科书 数学 七年级 上册课件说明 本节课主要学习角的比较,角的和差,角平分线.角的比较,角的和差,角平分线是本章重要的几何基础知识,也是后续学习图形与几何必备的知识基础.学习目标:
1. 理解角的大小、和差、角平分线的几何意义及数量关系,并会用文字语言、图形语言、符号语言进行综合描述.
2. 经历类比线段的长短、和差、中点学习角的大小、和差、角平分线等过程,体会类比思想.温故知新,引入课题1.角是怎样形成的图形?2.请同学们回忆一下,前面我们学习了线段的哪些内容?3. 如图,已知线段AB、CD,你有哪些办法比较它们的大小?温故知新,引入课题1.叠合法2.度量法 类比线段大小的比较,你认为该如何比较两个角的大小?试着画图来解决.观察思考,探究新知1.度量法∠ABC >∠DEFBCA70°30°2.叠合法观察思考,探究新知步骤:
1. 将两个角的顶点及一边重合,
2. 两个角的另一边落在重合一边的同侧,3.由两个角的另一边的位置确定两个角的
大小. 1. 如果EC与OD重合,那么∠AEC等于
∠BOD,记作∠AEC=∠BOD. 2.如果EC落在∠BOD的内部,那么∠AEC小
于∠BOD,记作∠AEC<∠BOD. 3.如果EC落在∠BOD的外部,那∠AEC
大于∠BOD,记作∠AEC>∠BOD.你能总结出两个角的大小关系有几种吗? 问题1
图中共有几个角?它们之间有什么关系?答:有三个角,关系是:∠BOC是 ∠AOC与 ∠AOB的差,记作 ∠BOC=∠AOC-∠AOB.∠AOC是∠AOB与 ∠BOC的和,记作 ∠AOC=∠AOB+∠BOC,∠AOB是 ∠AOC与 ∠BOC的差,记作 ∠AOB=∠AOC-∠BOC,观察思考,探究新知问题2
利用一副三角板,你能画出哪些度数的角?这些角有什么规律?观察思考,探究新知 问题3
如图,如果∠AOB=∠BOC,那么
∠AOC=2∠AOB=2 ,
∠AOB=∠BOC= .∠AOC∠BOC我们把射线OB叫做∠AOC的角平分线. 类比线段中点的定义,你能给角平分线下定义吗? 从一个角的顶点出发,把这个角分成相等的两个角的射线,叫这个角的平分线.观察思考,探究新知角的三等分线角的四等分线 问题4
如何作一个角的平分线?你能想到什么方法?度量法折纸法1.估计图中∠1与∠2的大小关系,
并用适当的方法验证.练习巩固,应用新知 适当改变角的位置,可以用叠合法检验.2.如图,∠AOB=90o,OC平分∠AOB,OE平分∠AOD,若∠EOC=60o,∠AOC= , ∠AOE= , ∠EOD= .
练习巩固,应用新知 45o15o15o练习巩固,应用新知 3.如图所示:
(1)∠AOC是哪两个角的和?
∠AOC=∠AOB+∠BOC.
(2)∠AOB是哪两个角的差?
∠AOB=∠AOC-∠BOC或∠AOD-∠BOD.
(3)如果∠AOB=∠COD,则∠AOC与∠BOD的大小关系如何?∠AOC=∠BOD.今天你学到了哪些知识?小结与回顾作业:
教科书习题4.3第4,5,6题.下节课我们继续学习!再见
