第四章 指数函数与对数函数 单元检测(含解析)
文档属性
| 名称 | 第四章 指数函数与对数函数 单元检测(含解析) | 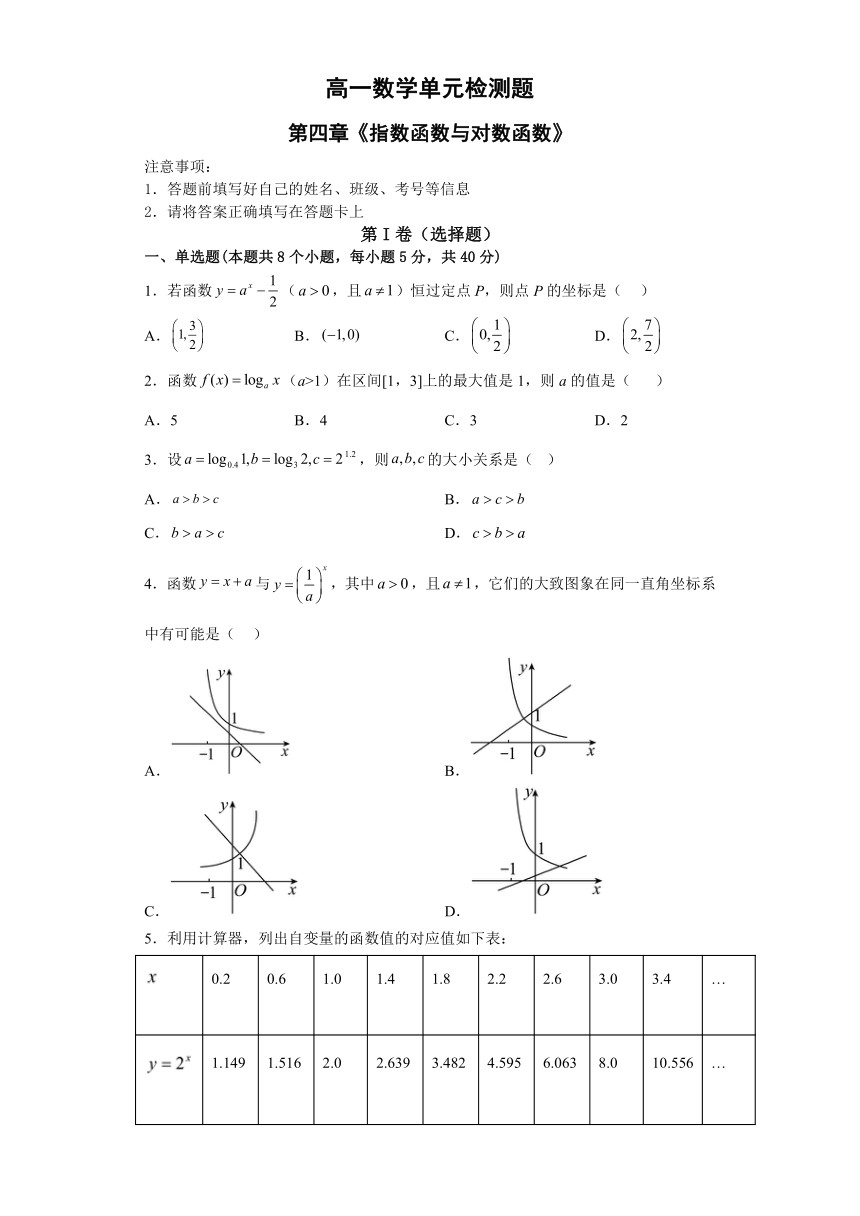 | |
| 格式 | docx | ||
| 文件大小 | 589.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-09 20:19:21 | ||
图片预览





文档简介
高一数学单元检测题
第四章《指数函数与对数函数》
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题(本题共8个小题,每小题5分,共40分)
1.若函数(,且)恒过定点P,则点P的坐标是( )
A. B. C. D.
2.函数(a>1)在区间[1,3]上的最大值是1,则a的值是( )
A.5 B.4 C.3 D.2
3.设,则的大小关系是( )
A. B.
C. D.
4.函数与,其中,且,它们的大致图象在同一直角坐标系中有可能是( )
A. B.
C. D.
5.利用计算器,列出自变量的函数值的对应值如下表:
0.2 0.6 1.0 1.4 1.8 2.2 2.6 3.0 3.4 …
1.149 1.516 2.0 2.639 3.482 4.595 6.063 8.0 10.556 …
0.04 0.36 1.0 1.96 3.24 4.84 6.76 9.0 11.56 …
那么方程的一个根位于下列区间 A.(0.6,1.0) B.(1.4,1.8) C.(1.8,2.2) D.(2.6,3.0)
6.如图,某池塘里浮萍的面积(单位:)与时间t(单位:月)的关系为,关于下列说法不正确的是( )
A.浮萍每月的增长率为2
B.浮萍每月增加的面积都相等
C.第4个月时,浮萍面积超过
D.若浮萍蔓延到所经过的时间分别是,、,则
7.已知是奇函数,且当时,.若,则( )
A. B. C. D.
8.函数f(x)=的零点个数是
A.1 B.2 C.3 D.4
二、多选题(本题共4个小题,每小题5分,共20分)
9.对于函数定义域内的任意(),当时,下述结论中正确的是( ).
A.
B.
C.
D.
10.下列说法正确的是( )
A.函数在定义域上是减函数
B.函数有且只有两个零点
C.函数的最小值是1
D.在同一坐标系中函数与的图象关于轴对称
11.若函数(,)在区间上的最大值与最小值的差为,则实数的值为( ).
A. B. C. D.
12.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设,用表示不超过的最大整数,则称为高斯函数,例如:,.已知函数,则关于函数的叙述中正确的是( )
A.是偶函数 B.是奇函数
C.在上是增函数 D.的值域是
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题(本题共4个小题,每小题5分,共20分)
13.四人赛跑,假设其跑过的路程和时间的函数关系分别是:①,②,③,④.如果他们一直跑下去,最终跑在最前面的人具有的函数关系是____.(只要填序号)
14.函数y=loga(2x-3)+8的图象恒过定点A,且点A在幂函数f(x)的图象上,则f(3)=________.
15.若,,则________.
16.已知函数,,则________.
四、解答题(本题共6个小题,共70分)
17.计算下列各式的值:
(1);
(2).
18.已知函数(且)的图象经过点和.
(1)求的解析式;
(2),求实数x的值;
19.已知f(x)=ax,g(x)=(a>0,且a≠1).
(1)讨论函数f(x)和g(x)的单调性;
(2)如果f(x)20.已知函数,,设.
(1)求的定义域;
(2)判断的奇偶性,并说明理由;
(3)若,求x的范围.
21.已知函数的图像恒过定点,且点又在函数的图像上.
(1)求实数的值;
(2)解不等式;
(3)有两个不等实根时,求的取值范围.
22.通过市场调查,得到某种纪念章每1枚的市场价y(单位:元)与上市时间x(单位:天)的数据如下表:
上市时间x/天 4 10 36
市场价y/元 90 51 90
(1)根据表中数据,从下列函数中选取一个恰当的函数描述该纪念章的市场价y与上市时间x的变化关系:
①y=ax+b;②y=ax2+bx+c;③y=alogbx.
(2)利用你选取的函数,求该纪念章市场价最低时的上市天数及最低的价格.
(3)设你选取的函数为f(x),若对任意实数k,方程f(x)=kx+2m+120恒有两个相异的实根,求m的取值范围.
高一数学单元检测题
第四章《指数函数与对数函数》
参考答案:
1.C【详解】当时,,所以函数(,且)恒过定点
2.C【详解】因为,所以函数在区间[1,3]上为增函数,
因为函数(a>1)在区间[1,3]上的最大值是1,
所以,解得,
3.D【详解】因,则,
函数在上单调递增,,于是有,即,
函数在R上单调递增,,则,即,
所以的大小关系是.
4.B【详解】对于A,C,由于函数是增函数,图象应该呈上升趋势,所以A,C错误;
对于B,若函数的图象是正确的,则,所以,所以函数是正确的,所以B正确;
对于D,若函数的图象是正确的,则,所以,所以函数是增函数,所以D错误,
5.C【详解】构造f(x)=2x-x2,则f(1.8)=0.242,f(2.2)=-0.245,故在(1.8,2.2)内存在一点使f(x)=2x-x2=0,所以方程2x=x2的一个根就位于区间(1.8,2.2)上.选C
点睛:判断函数零点(方程的根)所在区间的方法
6.B【详解】图象可知,函数过点,
,函数解析式为,
浮萍每月的增长率为,故选项A正确,
函数是指数函数,是曲线型函数,浮萍每月增加的面积不相等,故选项B错误,
当时,,故选项C正确,
对于D选项,,,,,
又,,故选项D正确,
7.B【详解】是奇函数,且当时,.若,
,则,得,
得,即,得,得,
8.C【详解】对于函数的零点个数
转化为方程的根的个数问题,分别画出左右两式表示的函数:如图.
由图象可得两个函数有两个交点.
又一次函数的根的个数是:1.
故函数的零点个数为3
9.CD【详解】A选项,函数的定义域为,故无意义,错,
B选项,,,而,错,
C选项,,对,
D选项,在单调递增,则,对,
10.CD【详解】对于A,在定义域上不具有单调性,故命题错误;
对于B,函数有三个零点,一个负值,两个正值,故命题错误;
对于C,∵|x|≥0,∴2|x|≥20=1,∴函数y=2|x|的最小值是1,故命题正确;
对于D,在同一坐标系中,函数y=2x与y=2﹣x的图象关于y轴对称,命题正确.
11.CD【详解】当时,在上单调递增,
此时,解得:,
当时,在上单调递减,
此时,解得:,
所以则实数的值为或,
12.BC【详解】根据题意知,.
∵,
,
,
∴函数既不是奇函数也不是偶函数,A错误;
,
∴是奇函数,B正确;
在R上是增函数,由复合函数的单调性知在R上是增函数,C正确;
,,,
,,D错误.
13.④【详解】由函数的性质可知,指数函数的增长速度是先慢后快,最终跑在最前面的是指数函数,所以最终跑在最前面的人具有的函数关系是④,
故答案为:④
14.27【详解】由题意,,则,定点A为(2,8),
设f(x)=xα,则2α=8,α=3,∴f(x)=x3,∴f(3)=33=27.
故答案为:27
15.1【详解】由可得,
又,
所以.
故答案为:.
16.【详解】因为,
,且,则.
17.解:
(1) ;
(2).
18.【详解】(1)由已知得,,,(且)
解得,;
故;
(2),即或3,
∴或3,
∴或16.
19.【详解】(1)当a>1时,f (x)=ax是R上的增函数,
由于0<<1,所以g(x)=是R上的减函数;
当0由于>1,所以g(x)=是R上的增函数;
(2),
当a>1时,x<0;当00.
∴当a>1时,x的取值范围是;
当020.【详解】(1)根据题意,函数,,
可得,
则有,解可得,即函数的定义域为;
(2)由(1)知,函数,
其定义域为,关于原点对称,
又由,
即,所以函数为定义域上的奇函数.
(3)由,即,
则满足且,解可得,
所以x的取值范围为.
21.【详解】(1)函数的图像恒过定点A,A点的坐标为(2, 2)
又因为A点在上,则:
(2)由题意知:
而在定义域上单调递增,知
,即
∴不等式的解集为
(3)由知:,方程有两个不等实根
若令,有它们的函数图像有两个交点,如下图示
由图像可知:,故b的取值范围为
22.【详解】(1)∵随着时间x的增加,y的值先减少后增加,而在所给的三个函数中y=ax+b和y=alogbx显然都是单调函数,不满足题意,
∴y=ax2+bx+c最合适.
(2)把点(4,90),(10,51),(36,90)代入方程,得
解方程组,得
∴y=x2-10x+126= (x-20)2+26.
∴当x=20时,y有最小值,ymin=26.
故该纪念章市场价最低时的上市天数为20,最低价格为26元.
(3)由(2)知f(x)=x2-10x+126,
∵f(x)=kx+2m+120恒有两个相异的实根,
则x2-(k+10)x+6-2m=0恒有两个相异的实根,
∴Δ=[-(k+10)]2-4×(6-2m)>0恒成立,
即2m>-(k+10)2+6对任意k∈R恒成立,而-(k+10)2+6≤6,
∴只需2m>6,即m>3.
故m的取值范围为(3,+∞).
第四章《指数函数与对数函数》
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题(本题共8个小题,每小题5分,共40分)
1.若函数(,且)恒过定点P,则点P的坐标是( )
A. B. C. D.
2.函数(a>1)在区间[1,3]上的最大值是1,则a的值是( )
A.5 B.4 C.3 D.2
3.设,则的大小关系是( )
A. B.
C. D.
4.函数与,其中,且,它们的大致图象在同一直角坐标系中有可能是( )
A. B.
C. D.
5.利用计算器,列出自变量的函数值的对应值如下表:
0.2 0.6 1.0 1.4 1.8 2.2 2.6 3.0 3.4 …
1.149 1.516 2.0 2.639 3.482 4.595 6.063 8.0 10.556 …
0.04 0.36 1.0 1.96 3.24 4.84 6.76 9.0 11.56 …
那么方程的一个根位于下列区间 A.(0.6,1.0) B.(1.4,1.8) C.(1.8,2.2) D.(2.6,3.0)
6.如图,某池塘里浮萍的面积(单位:)与时间t(单位:月)的关系为,关于下列说法不正确的是( )
A.浮萍每月的增长率为2
B.浮萍每月增加的面积都相等
C.第4个月时,浮萍面积超过
D.若浮萍蔓延到所经过的时间分别是,、,则
7.已知是奇函数,且当时,.若,则( )
A. B. C. D.
8.函数f(x)=的零点个数是
A.1 B.2 C.3 D.4
二、多选题(本题共4个小题,每小题5分,共20分)
9.对于函数定义域内的任意(),当时,下述结论中正确的是( ).
A.
B.
C.
D.
10.下列说法正确的是( )
A.函数在定义域上是减函数
B.函数有且只有两个零点
C.函数的最小值是1
D.在同一坐标系中函数与的图象关于轴对称
11.若函数(,)在区间上的最大值与最小值的差为,则实数的值为( ).
A. B. C. D.
12.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设,用表示不超过的最大整数,则称为高斯函数,例如:,.已知函数,则关于函数的叙述中正确的是( )
A.是偶函数 B.是奇函数
C.在上是增函数 D.的值域是
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题(本题共4个小题,每小题5分,共20分)
13.四人赛跑,假设其跑过的路程和时间的函数关系分别是:①,②,③,④.如果他们一直跑下去,最终跑在最前面的人具有的函数关系是____.(只要填序号)
14.函数y=loga(2x-3)+8的图象恒过定点A,且点A在幂函数f(x)的图象上,则f(3)=________.
15.若,,则________.
16.已知函数,,则________.
四、解答题(本题共6个小题,共70分)
17.计算下列各式的值:
(1);
(2).
18.已知函数(且)的图象经过点和.
(1)求的解析式;
(2),求实数x的值;
19.已知f(x)=ax,g(x)=(a>0,且a≠1).
(1)讨论函数f(x)和g(x)的单调性;
(2)如果f(x)
(1)求的定义域;
(2)判断的奇偶性,并说明理由;
(3)若,求x的范围.
21.已知函数的图像恒过定点,且点又在函数的图像上.
(1)求实数的值;
(2)解不等式;
(3)有两个不等实根时,求的取值范围.
22.通过市场调查,得到某种纪念章每1枚的市场价y(单位:元)与上市时间x(单位:天)的数据如下表:
上市时间x/天 4 10 36
市场价y/元 90 51 90
(1)根据表中数据,从下列函数中选取一个恰当的函数描述该纪念章的市场价y与上市时间x的变化关系:
①y=ax+b;②y=ax2+bx+c;③y=alogbx.
(2)利用你选取的函数,求该纪念章市场价最低时的上市天数及最低的价格.
(3)设你选取的函数为f(x),若对任意实数k,方程f(x)=kx+2m+120恒有两个相异的实根,求m的取值范围.
高一数学单元检测题
第四章《指数函数与对数函数》
参考答案:
1.C【详解】当时,,所以函数(,且)恒过定点
2.C【详解】因为,所以函数在区间[1,3]上为增函数,
因为函数(a>1)在区间[1,3]上的最大值是1,
所以,解得,
3.D【详解】因,则,
函数在上单调递增,,于是有,即,
函数在R上单调递增,,则,即,
所以的大小关系是.
4.B【详解】对于A,C,由于函数是增函数,图象应该呈上升趋势,所以A,C错误;
对于B,若函数的图象是正确的,则,所以,所以函数是正确的,所以B正确;
对于D,若函数的图象是正确的,则,所以,所以函数是增函数,所以D错误,
5.C【详解】构造f(x)=2x-x2,则f(1.8)=0.242,f(2.2)=-0.245,故在(1.8,2.2)内存在一点使f(x)=2x-x2=0,所以方程2x=x2的一个根就位于区间(1.8,2.2)上.选C
点睛:判断函数零点(方程的根)所在区间的方法
6.B【详解】图象可知,函数过点,
,函数解析式为,
浮萍每月的增长率为,故选项A正确,
函数是指数函数,是曲线型函数,浮萍每月增加的面积不相等,故选项B错误,
当时,,故选项C正确,
对于D选项,,,,,
又,,故选项D正确,
7.B【详解】是奇函数,且当时,.若,
,则,得,
得,即,得,得,
8.C【详解】对于函数的零点个数
转化为方程的根的个数问题,分别画出左右两式表示的函数:如图.
由图象可得两个函数有两个交点.
又一次函数的根的个数是:1.
故函数的零点个数为3
9.CD【详解】A选项,函数的定义域为,故无意义,错,
B选项,,,而,错,
C选项,,对,
D选项,在单调递增,则,对,
10.CD【详解】对于A,在定义域上不具有单调性,故命题错误;
对于B,函数有三个零点,一个负值,两个正值,故命题错误;
对于C,∵|x|≥0,∴2|x|≥20=1,∴函数y=2|x|的最小值是1,故命题正确;
对于D,在同一坐标系中,函数y=2x与y=2﹣x的图象关于y轴对称,命题正确.
11.CD【详解】当时,在上单调递增,
此时,解得:,
当时,在上单调递减,
此时,解得:,
所以则实数的值为或,
12.BC【详解】根据题意知,.
∵,
,
,
∴函数既不是奇函数也不是偶函数,A错误;
,
∴是奇函数,B正确;
在R上是增函数,由复合函数的单调性知在R上是增函数,C正确;
,,,
,,D错误.
13.④【详解】由函数的性质可知,指数函数的增长速度是先慢后快,最终跑在最前面的是指数函数,所以最终跑在最前面的人具有的函数关系是④,
故答案为:④
14.27【详解】由题意,,则,定点A为(2,8),
设f(x)=xα,则2α=8,α=3,∴f(x)=x3,∴f(3)=33=27.
故答案为:27
15.1【详解】由可得,
又,
所以.
故答案为:.
16.【详解】因为,
,且,则.
17.解:
(1) ;
(2).
18.【详解】(1)由已知得,,,(且)
解得,;
故;
(2),即或3,
∴或3,
∴或16.
19.【详解】(1)当a>1时,f (x)=ax是R上的增函数,
由于0<<1,所以g(x)=是R上的减函数;
当0
(2),
当a>1时,x<0;当0
∴当a>1时,x的取值范围是;
当0
可得,
则有,解可得,即函数的定义域为;
(2)由(1)知,函数,
其定义域为,关于原点对称,
又由,
即,所以函数为定义域上的奇函数.
(3)由,即,
则满足且,解可得,
所以x的取值范围为.
21.【详解】(1)函数的图像恒过定点A,A点的坐标为(2, 2)
又因为A点在上,则:
(2)由题意知:
而在定义域上单调递增,知
,即
∴不等式的解集为
(3)由知:,方程有两个不等实根
若令,有它们的函数图像有两个交点,如下图示
由图像可知:,故b的取值范围为
22.【详解】(1)∵随着时间x的增加,y的值先减少后增加,而在所给的三个函数中y=ax+b和y=alogbx显然都是单调函数,不满足题意,
∴y=ax2+bx+c最合适.
(2)把点(4,90),(10,51),(36,90)代入方程,得
解方程组,得
∴y=x2-10x+126= (x-20)2+26.
∴当x=20时,y有最小值,ymin=26.
故该纪念章市场价最低时的上市天数为20,最低价格为26元.
(3)由(2)知f(x)=x2-10x+126,
∵f(x)=kx+2m+120恒有两个相异的实根,
则x2-(k+10)x+6-2m=0恒有两个相异的实根,
∴Δ=[-(k+10)]2-4×(6-2m)>0恒成立,
即2m>-(k+10)2+6对任意k∈R恒成立,而-(k+10)2+6≤6,
∴只需2m>6,即m>3.
故m的取值范围为(3,+∞).
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
