第一章集合与函数的概念 综合复习讲义(含答案)
文档属性
| 名称 | 第一章集合与函数的概念 综合复习讲义(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 518.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-09 20:35:44 | ||
图片预览





文档简介
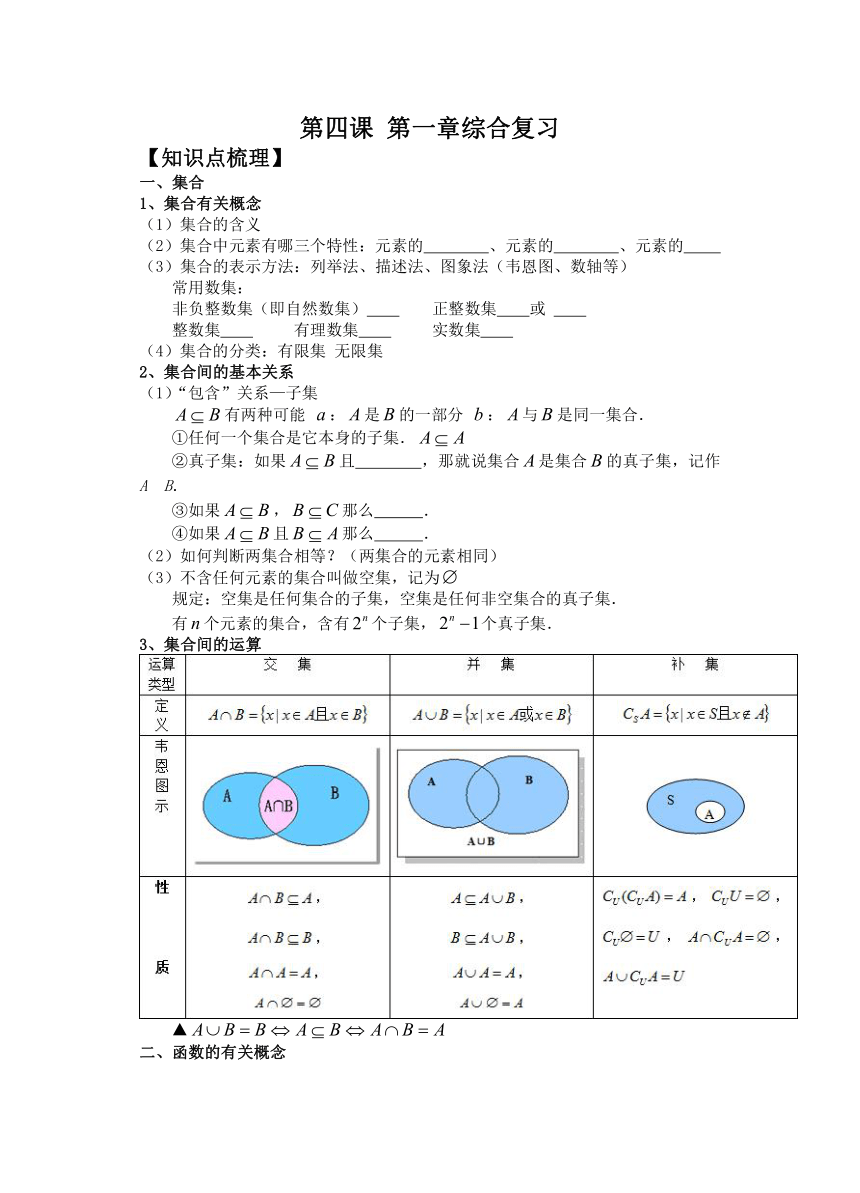
第四课 第一章综合复习
【知识点梳理】
一、集合
1、集合有关概念
(1)集合的含义
(2)集合中元素有哪三个特性:元素的 、元素的 、元素的
集合的表示方法:列举法、描述法、图象法(韦恩图、数轴等)
常用数集:
非负整数集(即自然数集) 正整数集 或
整数集 有理数集 实数集
(4)集合的分类:有限集 无限集
2、集合间的基本关系
(1)“包含”关系—子集
有两种可能 :是的一部分 :与是同一集合.
①任何一个集合是它本身的子集.
②真子集:如果且 ,那就说集合是集合的真子集,记作AB.
③如果,那么 .
④如果且那么 .
(2)如何判断两集合相等?(两集合的元素相同)
(3)不含任何元素的集合叫做空集,记为
规定:空集是任何集合的子集,空集是任何非空集合的真子集.
有个元素的集合,含有个子集,个真子集.
3、集合间的运算
▲
二、函数的有关概念
1、函数的概念
2、定义域:能使函数式有意义的实数的集合称为函数的定义域(或题意直接给出).
求函数的定义域有哪些常见类型?
(1)分式的分母 ;
(2)偶次方根的被开方数 ;
(3)对数式的真数必须 ;
(4)指数、对数式的底必须 且 ;
(5)零次幂的指数不可以 ;
(6)如果函数是由一些基本函数通过四则运算结合而成的,那么它的定义域是使各部分都有意义的的值组成的集合;
(7)已知的定义域为,求的定义域,只需;已知的定义域,则的定义域为的值域;
(8)实际问题中的函数的定义域还要保证实际问题有意义.
相同函数的判断方法:①表达式相同(与表示自变量和函数值的字母无关);②定义域一致 (两点必须同时具备)
3、函数的解析表达式
(1)函数的解析式是函数的一种表示方法,要求两个变量之间的函数关系时,一是要求出它们之间的对应法则,二是要求出函数的定义域.
(2)求函数的解析式的方法
①待定系数法②换元法③消元法(方程组法)④赋值法
三、函数的性质
1、函数的单调性
(1)增函数与减函数的定义(可用于判断函数的单调性)
(2)图象的特点
如果函数在某个区间是增函数或减函数,那么说函数在这一区间上具有(严格的)单调性,在单调区间上增函数的图象从左到右是 的,减函数的图象从左到右是 的.
(3)函数单调区间与单调性的判定方法
(A)定义法
①任取,且;
②作差;
③变形(通常是因式分解和配方);
④定号(即判断差的正负);
⑤下结论(指出函数在给定的区间上的单调性).
(B)观察图象法(从图象上看升降)
(C)复合函数的单调性:“同增异减”
(D)利用函数的运算性质(在公共定义域内)
增+增=增;减+减=减;增-减=增;减-增=减
注意:函数的单调区间只能是其定义域的子区间,不能把单调性相同的区间和在一起写成其并集.
2、函数的最值(值域)
①图象法②单调性法③反函数法④配方法⑤判别式法⑥换元法(⑦不等式法⑧数形结合法)
3、函数的奇偶性
(1)偶函数
一般地,对于函数的定义域内的任意一个,都有 ,那么就叫做偶函数.
(2)奇函数
一般地,对于函数的定义域内的任意一个,都有 ,那么就叫做奇函数.
(3)具有奇偶性的函数的图象的特征
偶函数的图象关于轴对称;奇函数的图象关于原点对称.特别地,如果奇函数的定义域包含有0,则 .
利用定义判断函数奇偶性的步骤:
①首先确定函数的定义域,并判断其是否关于原点对称;
②确定与的关系;
③作出相应结论:若或,则是偶函数;若或,则是奇函数.
【典型例题】
题型一 集合的基本关系与运算
例题1:已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},若B A,求实数m的取值范围.
例题2:已知方程x2+px+q=0的两个不相等实根分别为α,β,集合A={α,β},B={2,4,5,6},C={1,2,3,4},A∩C=A,A∩B=.求p,q的值.
变式1:已知集合A={x|2a+1≤x≤3a-5},B={x|x<-1,或x>16},分别根据下列条件求实数a的取值范围.
(1)A∩B=;(2)A (A∩B).
题型二 函数的定义域、值域
例题3:函数y=+的定义域为( )
A.{x|x≤1} B.{x|x≥0} C.{x|x≥1或x≤0} D.{x|0≤x≤1}
例题4:画出函数f(x)=-x2+2x+3的图象,并根据图象回答下列问题:
(1)比较f(0)、f(1)、f(3)的大小;
(2)若x1(3)求函数f(x)的值域.
题型三 函数的表达式、分段函数
例题5:如果f()=,则当x≠0,1时,f(x)等于( )
A. B. C. D.-1
例题6:已知f(x)=,
(1)画出f(x)的图象;
(2)求f(x)的定义域和值域.
题型四 函数的单调性、奇偶性
例题7:已知f(x)=,试判断f(x)在[1,+∞)上的单调性,并证明.
例题8:判断下列函数的奇偶性:
(1)f(x)=3,x∈R;
(2)f(x)=5x4-4x2+7,x∈[-3,3];
(3)f(x)=|2x-1|-|2x+1|;
(4)f(x)=
变式2:已知函数f(x)=x2-2x+2.
(1)求f(x)在区间[,3]上的最大值和最小值;
(2)若g(x)=f(x)-mx在[2,4]上是单调函数,求m的取值范围.
变式3:已知函数f(x)=1-.
(1)若g(x)=f(x)-a为奇函数,求a的值;
(2)试判断f(x)在(0,+∞)内的单调性,并用定义证明.
高中数学必修一第一章阶段检测
一:选择题(每小题5分,共50分)
1.已知集合则( )
A. B. C. D.
2.设全集,集合,,则=( )
A. B. C. D.
3.设:→是集合到集合的映射,若,,则=( )
A. B. C. D.
4.函数的定义域是( )
A. B. C. D.
5.设,则的值为( )
A. B. C. D.
6.若函数为偶函数,则=( )
A. B. C. D.
7.函数的图象是( )
8.若奇函数在区间上是增函数且最小值为,则在区间上是( )
A.增函数且最大值为 B.增函数且最小值为
C.减函数且最小值为 D.减函数且最大值为
9.某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了,再走余下的路,下图中轴表示离学校的距离,轴表示出发后的时间,则适合题意的图形是( )
10.若二次函数在区间上为减函数,那么( )
A. B. C. D.
二:填空题(每小题5分,共20分)
11.若集合满足,则集合的个数为_____________.
12.已知函数,若,则=_____________.
13.已知函数,若,则_____________.
14.函数在区间上具有单调性,则的取值范围为_____________.
三:解答题(本大题共6小题,满分80分)
15.(本小题满分12分) 设集合,, .
(1)求;
(2)求;
(3)若,求实数的取值范围.
16.(本小题满分12分) 已知二次函数满足:,且.
(1)求的解析式;
(2)求在区间上的最大值与最小值.
17.(本小题满分14分)已知函数,且,.
(1)求、的值;
(2)判断函数的奇偶性;
(3)判断在上的单调性并加以证明.
18.(本小题满分14分)已知是定义在上的奇函数,当时,.
(1)求及的值;
(2)求的解析式并画出简图;
(3)写出的单调区间(不用证明).
19.(本小题满分14分)某商品进货单价为元,若销售价为元,可卖出个,如果销售单价每涨元,销售量就减少个,为了获得最大利润,则此商品的最佳售价应为多少?并求出最大利润.
20.(本小题满分14分)已知函数.
(1)讨论函数的单调性;
(2)解关于的方程;
(3)当时,在上的最小值为,求的值.
参考答案:
【典型例题】
题型一 集合的基本关系与运算
例题1:已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},若B A,求实数m的取值范围.
【解析】A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},且B A.
①若B=,则m+1>2m-1,解得m<2,此时有B A;
②若B≠ ,则m+1≤2m-1,即m≥2,
由B A,得,解得2≤m≤3.
由①②得m≤3.
∴实数m的取值范围是{m|m≤3}.
例题2:已知方程x2+px+q=0的两个不相等实根分别为α,β,集合A={α,β},B={2,4,5,6},C={1,2,3,4},A∩C=A,A∩B=.求p,q的值.
【解析】由A∩C=A,A∩B=,可得:A={1,3},
即方程x2+px+q=0的两个实根为1,3.
∴,∴.
变式1:已知集合A={x|2a+1≤x≤3a-5},B={x|x<-1,或x>16},分别根据下列条件求实数a的取值范围.
(1)A∩B=;(2)A (A∩B).
【解析】(1)若A=,则A∩B=成立.
此时2a+1>3a-5,即a<6.
若A≠,如图所示,则
解得6≤a≤7.
综上,满足条件A∩B=的实数a的取值范围是{a|a≤7}.
(2)因为A (A∩B),且(A∩B) A,
所以A∩B=A,即A B.
显然A=满足条件,此时a<6.
若A≠,如图所示,则或
由解得a∈; 由解得a>.
综上,满足条件A (A∩B)的实数a的取值范围是{a|a<6或a>}.
题型二 函数的定义域、值域
例题3:函数y=+的定义域为( )
A.{x|x≤1} B.{x|x≥0} C.{x|x≥1或x≤0} D.{x|0≤x≤1}
【解析】D.
例题4:画出函数f(x)=-x2+2x+3的图象,并根据图象回答下列问题:
(1)比较f(0)、f(1)、f(3)的大小;
(2)若x1(3)求函数f(x)的值域.
【解析】因为函数f(x)=-x2+2x+3的定义域为R,列表:
x … -2 -1 0 1 2 3 4 …
y … -5 0 3 4 3 0 -5 …
连线,描点,得函数图象如图:
(1)根据图象,容易发现f(0)=3,f(1)=4,f(3)=0,
所以f(3)(2)根据图象,容易发现当x1(3)根据图象,可以看出函数的图象是以(1,4)为顶点,开口向下的抛物线,因此,函数的值域为(-∞,4].
题型三 函数的表达式、分段函数
例题5:如果f()=,则当x≠0,1时,f(x)等于( )
A. B. C. D.-1
【解析】B.
例题6:已知f(x)=,
(1)画出f(x)的图象;
(2)求f(x)的定义域和值域.
【解析】(1)利用描点法,作出f(x)的图象,如图所示.
(2)由条件知,函数f(x)的定义域为R.
由图象知,当-1≤x≤1时,f(x)=x2的值域为[0,1],
当x>1或x<-1时,f(x)=1,
所以f(x)的值域为[0,1].
题型四 函数的单调性、奇偶性
例题7:已知f(x)=,试判断f(x)在[1,+∞)上的单调性,并证明.
【解析】函数f(x)=在[1,+∞)上是增函数.
证明如下:
任取x1,x2∈[1,+∞),且x1则f(x2)-f(x1)=-
=
=.
∵1≤x1∴x2+x1>0,x2-x1>0,+>0.
∴f(x2)-f(x1)>0,即f(x2)>f(x1),
故函数f(x)在[1,+∞)上是增函数.
例题8:判断下列函数的奇偶性:
(1)f(x)=3,x∈R;
(2)f(x)=5x4-4x2+7,x∈[-3,3];
(3)f(x)=|2x-1|-|2x+1|;
(4)f(x)=
【解析】(1)f(-x)=3=f(x),∴f(x)是偶函数.
(2)∵x∈[-3,3],f(-x)=5(-x)4-4(-x)2+7=5x4-4x2+7=f(x),∴f(x)是偶函数.
(3)f(-x)=|-2x-1|-|-2x+1|=-(|2x-1|-|2x+1|)=-f(x),∴f(x)是奇函数.
(4)当x>0时,f(x)=1-x2,此时-x<0,
∴f(-x)=(-x)2-1=x2-1,∴f(-x)=-f(x);
当x<0时,f(x)=x2-1,此时-x>0,f(-x)=1-(-x)2=1-x2,
∴f(-x)=-f(x);
当x=0时,f(-0)=-f(0)=0.
综上,对x∈R,总有f(-x)=-f(x),
∴f(x)为R上的奇函数.
变式2:已知函数f(x)=x2-2x+2.
(1)求f(x)在区间[,3]上的最大值和最小值;
(2)若g(x)=f(x)-mx在[2,4]上是单调函数,求m的取值范围.
【解析】(1)∵f(x)=x2-2x+2=(x-1)2+1,x∈[,3],
∴f(x)的最小值是f(1)=1,
又f()=,f(3)=5,
所以f(x)在区间[,3]上的最大值是5,最小值是1.
(2)∵g(x)=f(x)-mx=x2-(m+2)x+2,
∴≤2或≥4,
即m≤2或m≥6.
故m的取值范围是(-∞,2]∪[6,+∞).
变式3:已知函数f(x)=1-.
(1)若g(x)=f(x)-a为奇函数,求a的值;
(2)试判断f(x)在(0,+∞)内的单调性,并用定义证明.
【解析】(1)由已知g(x)=f(x)-a得,g(x)=1-a-,
∵g(x)是奇函数,
∴g(-x)=-g(x),即1-a-=-(1-a-),解得a=1.
(2)函数f(x)在(0,+∞)内为增函数.
设0<x1<x2,则f(x1)-f(x2)
=1--(1-)=.
∵0<x1<x2,∴x1-x2<0,x1x2>0,从而<0,即f(x1)<f(x2).
所以函数f(x)在(0,+∞)内是单调增函数.
高中数学必修一第一章阶段检测参考答案
一:选择题(每小题5分,共50分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B B A C D A D B
二:填空题(每小题5分,共20分)
11.3 12.-13 13.-3 14.或
三:解答题(共80分)
15.(本小题满分12分)
(1) ……………2分
∴ ……………4分
(2)∵ ……………6分
∴ ……………8分
(3)∵,∴
∴,∴ ……………12分
16.(本小题满分12分)
(1)∵,∴, ……………1分
∴
∴ ………4分
∴
∴ ………………6分
(2) ……………8分
∵,∴在上是减函数,在上是增函数
又> …………………………………………10分
∴. ……………………12分
17.(本小题满分14分)
(1)依题意有, ……………2分
得 ……………………………………………4分
(2)的定义域为关于原点对称, ……………5分
∵ ∴函数为奇函数. ……7分
(3)设,且 ……………………………………………8分
…………………………………………………………………………………………11分
∵,且
∴,, ……………………………………………12分
∴,即 ……………………………………………13分
∴在上是增函数. ……………………………………………14分
18.(本小题满分14分)
(1)∵是定义在上的奇函数,
∴,∴, ………………………………………………………2分
∴当时,
∴ ………………………………………………………4分
(2)当时,
∴ ………………………………………………6分
∵是定义在上的奇函数,∴
∴,即()
∴的解析式为 …………………………………………8分
的图象如下图
………………………………………………10分
(3)由的图象可知:的增区间为,减区间为…14分
19.(本小题满分14分)
设商品的售价定为元,利润为元,则每件商品的利润为元,每件商品涨价了元,商品少卖了个,商品卖了个. ……3分
∴ ……………………………………7分
由,得
∴ ……………………………………10分
二次函数的对称轴为,且开口向下
∴当时,. ……………………………13分
答:商品的售价定为元时,销售利润最大,最大利润为元. ……………14分
(也可用配方法去求)
20.(本小题满分14分)
(1)当时,函数在上为减函数;……1分
当时,函数开口向上,对称轴为
∴函数在上为减函数,在上为增函数 ………………3分
当,函数开口向下,对称轴为
∴函数在上为增函数,在上为减函数 ………………5分
(2)方程,
当时,方程有1个实根, …………………6分
当时, …………………7分
①若,即时,方程没有实根 …………………8分
②若,即时,方程有1个实根 …………9分
③若,即,且时,方程有2个实根…10分
综上:当时,方程没有实根
当时,方程有1个实根
当时,方程有1个实根
当,且时,方程有2个实根 ………………11分
(3)当时,函数开口向上,对称轴为
∴在区间上为增函数 ………………12分
∴,得 ………………14分
【知识点梳理】
一、集合
1、集合有关概念
(1)集合的含义
(2)集合中元素有哪三个特性:元素的 、元素的 、元素的
集合的表示方法:列举法、描述法、图象法(韦恩图、数轴等)
常用数集:
非负整数集(即自然数集) 正整数集 或
整数集 有理数集 实数集
(4)集合的分类:有限集 无限集
2、集合间的基本关系
(1)“包含”关系—子集
有两种可能 :是的一部分 :与是同一集合.
①任何一个集合是它本身的子集.
②真子集:如果且 ,那就说集合是集合的真子集,记作AB.
③如果,那么 .
④如果且那么 .
(2)如何判断两集合相等?(两集合的元素相同)
(3)不含任何元素的集合叫做空集,记为
规定:空集是任何集合的子集,空集是任何非空集合的真子集.
有个元素的集合,含有个子集,个真子集.
3、集合间的运算
▲
二、函数的有关概念
1、函数的概念
2、定义域:能使函数式有意义的实数的集合称为函数的定义域(或题意直接给出).
求函数的定义域有哪些常见类型?
(1)分式的分母 ;
(2)偶次方根的被开方数 ;
(3)对数式的真数必须 ;
(4)指数、对数式的底必须 且 ;
(5)零次幂的指数不可以 ;
(6)如果函数是由一些基本函数通过四则运算结合而成的,那么它的定义域是使各部分都有意义的的值组成的集合;
(7)已知的定义域为,求的定义域,只需;已知的定义域,则的定义域为的值域;
(8)实际问题中的函数的定义域还要保证实际问题有意义.
相同函数的判断方法:①表达式相同(与表示自变量和函数值的字母无关);②定义域一致 (两点必须同时具备)
3、函数的解析表达式
(1)函数的解析式是函数的一种表示方法,要求两个变量之间的函数关系时,一是要求出它们之间的对应法则,二是要求出函数的定义域.
(2)求函数的解析式的方法
①待定系数法②换元法③消元法(方程组法)④赋值法
三、函数的性质
1、函数的单调性
(1)增函数与减函数的定义(可用于判断函数的单调性)
(2)图象的特点
如果函数在某个区间是增函数或减函数,那么说函数在这一区间上具有(严格的)单调性,在单调区间上增函数的图象从左到右是 的,减函数的图象从左到右是 的.
(3)函数单调区间与单调性的判定方法
(A)定义法
①任取,且;
②作差;
③变形(通常是因式分解和配方);
④定号(即判断差的正负);
⑤下结论(指出函数在给定的区间上的单调性).
(B)观察图象法(从图象上看升降)
(C)复合函数的单调性:“同增异减”
(D)利用函数的运算性质(在公共定义域内)
增+增=增;减+减=减;增-减=增;减-增=减
注意:函数的单调区间只能是其定义域的子区间,不能把单调性相同的区间和在一起写成其并集.
2、函数的最值(值域)
①图象法②单调性法③反函数法④配方法⑤判别式法⑥换元法(⑦不等式法⑧数形结合法)
3、函数的奇偶性
(1)偶函数
一般地,对于函数的定义域内的任意一个,都有 ,那么就叫做偶函数.
(2)奇函数
一般地,对于函数的定义域内的任意一个,都有 ,那么就叫做奇函数.
(3)具有奇偶性的函数的图象的特征
偶函数的图象关于轴对称;奇函数的图象关于原点对称.特别地,如果奇函数的定义域包含有0,则 .
利用定义判断函数奇偶性的步骤:
①首先确定函数的定义域,并判断其是否关于原点对称;
②确定与的关系;
③作出相应结论:若或,则是偶函数;若或,则是奇函数.
【典型例题】
题型一 集合的基本关系与运算
例题1:已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},若B A,求实数m的取值范围.
例题2:已知方程x2+px+q=0的两个不相等实根分别为α,β,集合A={α,β},B={2,4,5,6},C={1,2,3,4},A∩C=A,A∩B=.求p,q的值.
变式1:已知集合A={x|2a+1≤x≤3a-5},B={x|x<-1,或x>16},分别根据下列条件求实数a的取值范围.
(1)A∩B=;(2)A (A∩B).
题型二 函数的定义域、值域
例题3:函数y=+的定义域为( )
A.{x|x≤1} B.{x|x≥0} C.{x|x≥1或x≤0} D.{x|0≤x≤1}
例题4:画出函数f(x)=-x2+2x+3的图象,并根据图象回答下列问题:
(1)比较f(0)、f(1)、f(3)的大小;
(2)若x1
题型三 函数的表达式、分段函数
例题5:如果f()=,则当x≠0,1时,f(x)等于( )
A. B. C. D.-1
例题6:已知f(x)=,
(1)画出f(x)的图象;
(2)求f(x)的定义域和值域.
题型四 函数的单调性、奇偶性
例题7:已知f(x)=,试判断f(x)在[1,+∞)上的单调性,并证明.
例题8:判断下列函数的奇偶性:
(1)f(x)=3,x∈R;
(2)f(x)=5x4-4x2+7,x∈[-3,3];
(3)f(x)=|2x-1|-|2x+1|;
(4)f(x)=
变式2:已知函数f(x)=x2-2x+2.
(1)求f(x)在区间[,3]上的最大值和最小值;
(2)若g(x)=f(x)-mx在[2,4]上是单调函数,求m的取值范围.
变式3:已知函数f(x)=1-.
(1)若g(x)=f(x)-a为奇函数,求a的值;
(2)试判断f(x)在(0,+∞)内的单调性,并用定义证明.
高中数学必修一第一章阶段检测
一:选择题(每小题5分,共50分)
1.已知集合则( )
A. B. C. D.
2.设全集,集合,,则=( )
A. B. C. D.
3.设:→是集合到集合的映射,若,,则=( )
A. B. C. D.
4.函数的定义域是( )
A. B. C. D.
5.设,则的值为( )
A. B. C. D.
6.若函数为偶函数,则=( )
A. B. C. D.
7.函数的图象是( )
8.若奇函数在区间上是增函数且最小值为,则在区间上是( )
A.增函数且最大值为 B.增函数且最小值为
C.减函数且最小值为 D.减函数且最大值为
9.某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了,再走余下的路,下图中轴表示离学校的距离,轴表示出发后的时间,则适合题意的图形是( )
10.若二次函数在区间上为减函数,那么( )
A. B. C. D.
二:填空题(每小题5分,共20分)
11.若集合满足,则集合的个数为_____________.
12.已知函数,若,则=_____________.
13.已知函数,若,则_____________.
14.函数在区间上具有单调性,则的取值范围为_____________.
三:解答题(本大题共6小题,满分80分)
15.(本小题满分12分) 设集合,, .
(1)求;
(2)求;
(3)若,求实数的取值范围.
16.(本小题满分12分) 已知二次函数满足:,且.
(1)求的解析式;
(2)求在区间上的最大值与最小值.
17.(本小题满分14分)已知函数,且,.
(1)求、的值;
(2)判断函数的奇偶性;
(3)判断在上的单调性并加以证明.
18.(本小题满分14分)已知是定义在上的奇函数,当时,.
(1)求及的值;
(2)求的解析式并画出简图;
(3)写出的单调区间(不用证明).
19.(本小题满分14分)某商品进货单价为元,若销售价为元,可卖出个,如果销售单价每涨元,销售量就减少个,为了获得最大利润,则此商品的最佳售价应为多少?并求出最大利润.
20.(本小题满分14分)已知函数.
(1)讨论函数的单调性;
(2)解关于的方程;
(3)当时,在上的最小值为,求的值.
参考答案:
【典型例题】
题型一 集合的基本关系与运算
例题1:已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},若B A,求实数m的取值范围.
【解析】A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},且B A.
①若B=,则m+1>2m-1,解得m<2,此时有B A;
②若B≠ ,则m+1≤2m-1,即m≥2,
由B A,得,解得2≤m≤3.
由①②得m≤3.
∴实数m的取值范围是{m|m≤3}.
例题2:已知方程x2+px+q=0的两个不相等实根分别为α,β,集合A={α,β},B={2,4,5,6},C={1,2,3,4},A∩C=A,A∩B=.求p,q的值.
【解析】由A∩C=A,A∩B=,可得:A={1,3},
即方程x2+px+q=0的两个实根为1,3.
∴,∴.
变式1:已知集合A={x|2a+1≤x≤3a-5},B={x|x<-1,或x>16},分别根据下列条件求实数a的取值范围.
(1)A∩B=;(2)A (A∩B).
【解析】(1)若A=,则A∩B=成立.
此时2a+1>3a-5,即a<6.
若A≠,如图所示,则
解得6≤a≤7.
综上,满足条件A∩B=的实数a的取值范围是{a|a≤7}.
(2)因为A (A∩B),且(A∩B) A,
所以A∩B=A,即A B.
显然A=满足条件,此时a<6.
若A≠,如图所示,则或
由解得a∈; 由解得a>.
综上,满足条件A (A∩B)的实数a的取值范围是{a|a<6或a>}.
题型二 函数的定义域、值域
例题3:函数y=+的定义域为( )
A.{x|x≤1} B.{x|x≥0} C.{x|x≥1或x≤0} D.{x|0≤x≤1}
【解析】D.
例题4:画出函数f(x)=-x2+2x+3的图象,并根据图象回答下列问题:
(1)比较f(0)、f(1)、f(3)的大小;
(2)若x1
【解析】因为函数f(x)=-x2+2x+3的定义域为R,列表:
x … -2 -1 0 1 2 3 4 …
y … -5 0 3 4 3 0 -5 …
连线,描点,得函数图象如图:
(1)根据图象,容易发现f(0)=3,f(1)=4,f(3)=0,
所以f(3)
题型三 函数的表达式、分段函数
例题5:如果f()=,则当x≠0,1时,f(x)等于( )
A. B. C. D.-1
【解析】B.
例题6:已知f(x)=,
(1)画出f(x)的图象;
(2)求f(x)的定义域和值域.
【解析】(1)利用描点法,作出f(x)的图象,如图所示.
(2)由条件知,函数f(x)的定义域为R.
由图象知,当-1≤x≤1时,f(x)=x2的值域为[0,1],
当x>1或x<-1时,f(x)=1,
所以f(x)的值域为[0,1].
题型四 函数的单调性、奇偶性
例题7:已知f(x)=,试判断f(x)在[1,+∞)上的单调性,并证明.
【解析】函数f(x)=在[1,+∞)上是增函数.
证明如下:
任取x1,x2∈[1,+∞),且x1
=
=.
∵1≤x1
∴f(x2)-f(x1)>0,即f(x2)>f(x1),
故函数f(x)在[1,+∞)上是增函数.
例题8:判断下列函数的奇偶性:
(1)f(x)=3,x∈R;
(2)f(x)=5x4-4x2+7,x∈[-3,3];
(3)f(x)=|2x-1|-|2x+1|;
(4)f(x)=
【解析】(1)f(-x)=3=f(x),∴f(x)是偶函数.
(2)∵x∈[-3,3],f(-x)=5(-x)4-4(-x)2+7=5x4-4x2+7=f(x),∴f(x)是偶函数.
(3)f(-x)=|-2x-1|-|-2x+1|=-(|2x-1|-|2x+1|)=-f(x),∴f(x)是奇函数.
(4)当x>0时,f(x)=1-x2,此时-x<0,
∴f(-x)=(-x)2-1=x2-1,∴f(-x)=-f(x);
当x<0时,f(x)=x2-1,此时-x>0,f(-x)=1-(-x)2=1-x2,
∴f(-x)=-f(x);
当x=0时,f(-0)=-f(0)=0.
综上,对x∈R,总有f(-x)=-f(x),
∴f(x)为R上的奇函数.
变式2:已知函数f(x)=x2-2x+2.
(1)求f(x)在区间[,3]上的最大值和最小值;
(2)若g(x)=f(x)-mx在[2,4]上是单调函数,求m的取值范围.
【解析】(1)∵f(x)=x2-2x+2=(x-1)2+1,x∈[,3],
∴f(x)的最小值是f(1)=1,
又f()=,f(3)=5,
所以f(x)在区间[,3]上的最大值是5,最小值是1.
(2)∵g(x)=f(x)-mx=x2-(m+2)x+2,
∴≤2或≥4,
即m≤2或m≥6.
故m的取值范围是(-∞,2]∪[6,+∞).
变式3:已知函数f(x)=1-.
(1)若g(x)=f(x)-a为奇函数,求a的值;
(2)试判断f(x)在(0,+∞)内的单调性,并用定义证明.
【解析】(1)由已知g(x)=f(x)-a得,g(x)=1-a-,
∵g(x)是奇函数,
∴g(-x)=-g(x),即1-a-=-(1-a-),解得a=1.
(2)函数f(x)在(0,+∞)内为增函数.
设0<x1<x2,则f(x1)-f(x2)
=1--(1-)=.
∵0<x1<x2,∴x1-x2<0,x1x2>0,从而<0,即f(x1)<f(x2).
所以函数f(x)在(0,+∞)内是单调增函数.
高中数学必修一第一章阶段检测参考答案
一:选择题(每小题5分,共50分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B B A C D A D B
二:填空题(每小题5分,共20分)
11.3 12.-13 13.-3 14.或
三:解答题(共80分)
15.(本小题满分12分)
(1) ……………2分
∴ ……………4分
(2)∵ ……………6分
∴ ……………8分
(3)∵,∴
∴,∴ ……………12分
16.(本小题满分12分)
(1)∵,∴, ……………1分
∴
∴ ………4分
∴
∴ ………………6分
(2) ……………8分
∵,∴在上是减函数,在上是增函数
又> …………………………………………10分
∴. ……………………12分
17.(本小题满分14分)
(1)依题意有, ……………2分
得 ……………………………………………4分
(2)的定义域为关于原点对称, ……………5分
∵ ∴函数为奇函数. ……7分
(3)设,且 ……………………………………………8分
…………………………………………………………………………………………11分
∵,且
∴,, ……………………………………………12分
∴,即 ……………………………………………13分
∴在上是增函数. ……………………………………………14分
18.(本小题满分14分)
(1)∵是定义在上的奇函数,
∴,∴, ………………………………………………………2分
∴当时,
∴ ………………………………………………………4分
(2)当时,
∴ ………………………………………………6分
∵是定义在上的奇函数,∴
∴,即()
∴的解析式为 …………………………………………8分
的图象如下图
………………………………………………10分
(3)由的图象可知:的增区间为,减区间为…14分
19.(本小题满分14分)
设商品的售价定为元,利润为元,则每件商品的利润为元,每件商品涨价了元,商品少卖了个,商品卖了个. ……3分
∴ ……………………………………7分
由,得
∴ ……………………………………10分
二次函数的对称轴为,且开口向下
∴当时,. ……………………………13分
答:商品的售价定为元时,销售利润最大,最大利润为元. ……………14分
(也可用配方法去求)
20.(本小题满分14分)
(1)当时,函数在上为减函数;……1分
当时,函数开口向上,对称轴为
∴函数在上为减函数,在上为增函数 ………………3分
当,函数开口向下,对称轴为
∴函数在上为增函数,在上为减函数 ………………5分
(2)方程,
当时,方程有1个实根, …………………6分
当时, …………………7分
①若,即时,方程没有实根 …………………8分
②若,即时,方程有1个实根 …………9分
③若,即,且时,方程有2个实根…10分
综上:当时,方程没有实根
当时,方程有1个实根
当时,方程有1个实根
当,且时,方程有2个实根 ………………11分
(3)当时,函数开口向上,对称轴为
∴在区间上为增函数 ………………12分
∴,得 ………………14分
