苏教版(2019)高中数学必修第二册 第9章 平面向量 章末复习课 课件(共35张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学必修第二册 第9章 平面向量 章末复习课 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-10 10:01:59 | ||
图片预览







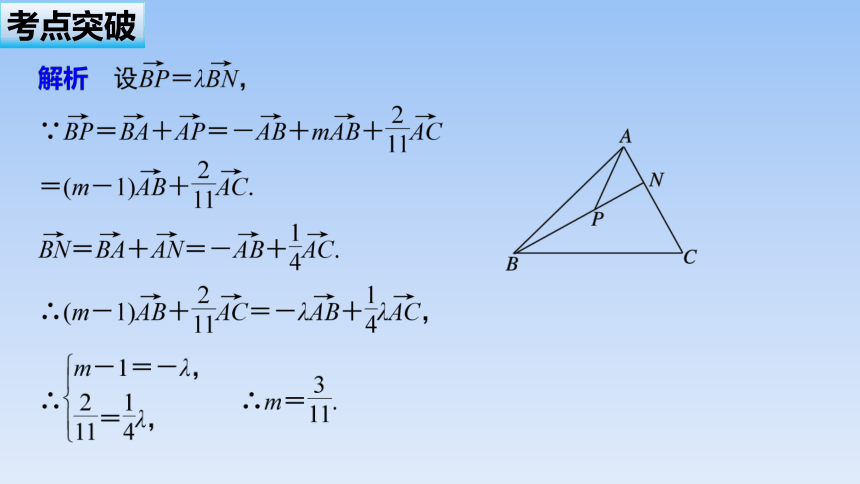


文档简介
(共35张PPT)
章末复习课
第九章 平面向量
内
容
索
引
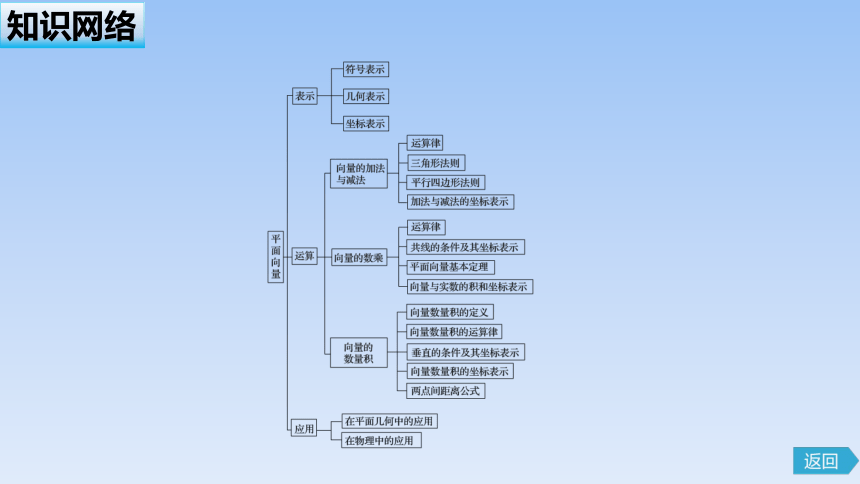
知识网络
考点突破
真题体验
1
知识网络
PART ONE
知识网络
2
考点突破
PART TWO
一、向量的线性运算
1.向量的线性运算有平面向量及其坐标运算的加法、减法、数乘运算,以及平面向量的基本定理、共线定理,主要考查向量的线性运算和根据线性运算求参问题.
2.通过向量的线性运算,培养数学运算和逻辑推理素养.
考点突破
例1 (1)已知向量a=(2,1),b=(-3,4),则2a-b等于
A.(7,-2) B.(1,-2)
C.(1,-3) D.(7,2)
解析 ∵a=(2,1),b=(-3,4),
∴2a-b=2(2,1)-(-3,4)=(4,2)-(-3,4)
=(4+3,2-4)=(7,-2).
√
考点突破
考点突破
考点突破
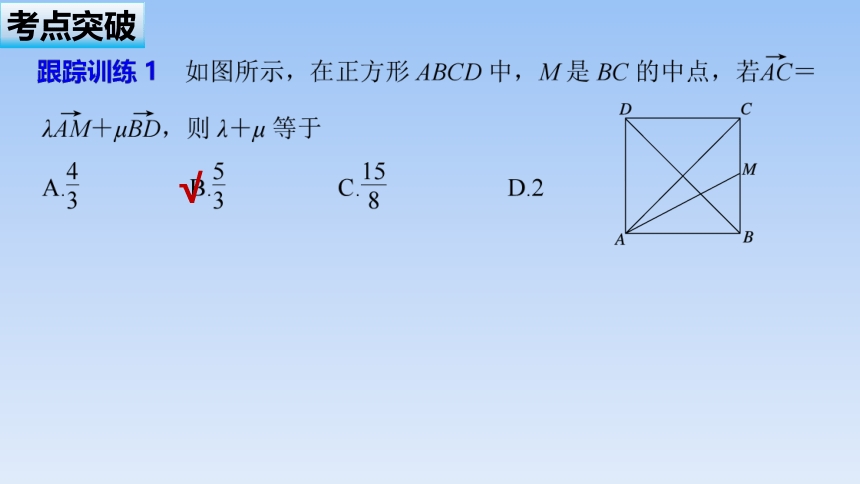
向量共线定理和平面向量基本定理是进行向量合成与分解的核心,是向量线性运算的关键所在,常应用它们解决平面几何中的共线、共点问题.
反思感悟
√
考点突破
考点突破
二、向量的数量积
1.向量的数量积是向量的核心内容,重点是数量积的运算,利用向量的数量积判断两向量平行、垂直,求两向量的夹角,计算向量的长度等.
2.通过向量的数量积运算,提升逻辑推理和数学运算素养.
考点突破
A.30° B.45° C.60° D.120°
√
考点突破
解析 设a与b的夹角为θ,
又|a-b|2=|a|2+|b|2-2a·b=1,
即1+|b|2-1=1,
故|b|=1. ②
又0°≤θ≤180°,所以θ=60°,故选C.
考点突破
9
考点突破
(1)向量数量积的两种计算方法
①当已知向量的模和夹角θ时,可利用定义法求解,即a·b=|a||b|cos θ;
②当已知向量的坐标时,可利用坐标法求解,即若a=(x1,y1),b=(x2,y2),则a·b=x1x2+y1y2.
(2)利用向量的数量积可以解决以下问题
①设a=(x1,y1),b=(x2,y2),
a∥b x1y2-x2y1=0,
a⊥b x1x2+y1y2=0(a,b均为非零向量);
反思感悟
②求向量的夹角和模的问题
两向量夹角的余弦值(0≤θ≤π,a,b为非零向量)
反思感悟
考点突破
三、向量坐标法在平面几何中的应用
1.向量在平面几何中的应用是用向量的线性运算及数量积解决平面几何中的平行、垂直、长度、夹角等问题.
2.对于有些平面图形的问题,常建立平面直角坐标系,转化为代数运算解决.考查学生转化与化归和数形结合的能力.
考点突破
考点突破
解析 作CO⊥AB于点O,建立如图所示的平面直角坐标系,
考点突破
把几何图形放到适当的坐标系中,就赋予了有关点与向量具体的坐标,这样就能进行相应的代数运算和向量运算,从而解决问题.这样的解题方法具有普遍性.
反思感悟
考点突破
解析 由题意,得∠AOC=90°,故以O为坐标原点,OC,OA所在直线分别为x轴,y轴建立平面直角坐标系,如图所示.
考点突破
3
真题体验
PART THREE
解析 作出示意图如图所示.
1.(2018·全国Ⅰ)在△ABC中,AD为BC边上的中线,E为AD的中点,则
√
1
2
3
4
5
真题体验
A.-3 B.-2 C.2 D.3
√
1
2
3
4
5
真题体验
3.(2019·全国Ⅰ)已知非零向量a,b满足|a|=2|b|,且(a-b)⊥b,则a与b的夹角为
√
解析 设a与b的夹角为α,∵(a-b)⊥b,∴(a-b)·b=0,
∴a·b=b2,∴|a|·|b|cos α=|b|2,又|a|=2|b|,
1
2
3
4
5
真题体验
1
2
3
4
5
4.(2020·全国Ⅱ)已知单位向量a,b的夹角为60°,则在下列向量中,与b垂直的是
A.a+2b B.2a+b C.a-2b D.2a-b
√
真题体验
1
2
3
4
5
解析 由题意得|a|=|b|=1,
设a,b的夹角为θ=60°,
真题体验
1
2
3
4
5
5.(2020·江苏)在△ABC中,AB=4,AC=3,∠BAC=90°,D在边BC
真题体验
解析 如图,以点A为坐标原点,AB,AC所在的直线分别为x轴、y轴建立平面直角坐标系,
1
2
3
4
5
真题体验
1
2
3
4
5
真题体验
1
2
3
4
5
∴P(0,9),此时C与D重合,CD=0.
真题体验
章末复习课
第九章 平面向量
内
容
索
引
知识网络
考点突破
真题体验
1
知识网络
PART ONE
知识网络
2
考点突破
PART TWO
一、向量的线性运算
1.向量的线性运算有平面向量及其坐标运算的加法、减法、数乘运算,以及平面向量的基本定理、共线定理,主要考查向量的线性运算和根据线性运算求参问题.
2.通过向量的线性运算,培养数学运算和逻辑推理素养.
考点突破
例1 (1)已知向量a=(2,1),b=(-3,4),则2a-b等于
A.(7,-2) B.(1,-2)
C.(1,-3) D.(7,2)
解析 ∵a=(2,1),b=(-3,4),
∴2a-b=2(2,1)-(-3,4)=(4,2)-(-3,4)
=(4+3,2-4)=(7,-2).
√
考点突破
考点突破
考点突破
向量共线定理和平面向量基本定理是进行向量合成与分解的核心,是向量线性运算的关键所在,常应用它们解决平面几何中的共线、共点问题.
反思感悟
√
考点突破
考点突破
二、向量的数量积
1.向量的数量积是向量的核心内容,重点是数量积的运算,利用向量的数量积判断两向量平行、垂直,求两向量的夹角,计算向量的长度等.
2.通过向量的数量积运算,提升逻辑推理和数学运算素养.
考点突破
A.30° B.45° C.60° D.120°
√
考点突破
解析 设a与b的夹角为θ,
又|a-b|2=|a|2+|b|2-2a·b=1,
即1+|b|2-1=1,
故|b|=1. ②
又0°≤θ≤180°,所以θ=60°,故选C.
考点突破
9
考点突破
(1)向量数量积的两种计算方法
①当已知向量的模和夹角θ时,可利用定义法求解,即a·b=|a||b|cos θ;
②当已知向量的坐标时,可利用坐标法求解,即若a=(x1,y1),b=(x2,y2),则a·b=x1x2+y1y2.
(2)利用向量的数量积可以解决以下问题
①设a=(x1,y1),b=(x2,y2),
a∥b x1y2-x2y1=0,
a⊥b x1x2+y1y2=0(a,b均为非零向量);
反思感悟
②求向量的夹角和模的问题
两向量夹角的余弦值(0≤θ≤π,a,b为非零向量)
反思感悟
考点突破
三、向量坐标法在平面几何中的应用
1.向量在平面几何中的应用是用向量的线性运算及数量积解决平面几何中的平行、垂直、长度、夹角等问题.
2.对于有些平面图形的问题,常建立平面直角坐标系,转化为代数运算解决.考查学生转化与化归和数形结合的能力.
考点突破
考点突破
解析 作CO⊥AB于点O,建立如图所示的平面直角坐标系,
考点突破
把几何图形放到适当的坐标系中,就赋予了有关点与向量具体的坐标,这样就能进行相应的代数运算和向量运算,从而解决问题.这样的解题方法具有普遍性.
反思感悟
考点突破
解析 由题意,得∠AOC=90°,故以O为坐标原点,OC,OA所在直线分别为x轴,y轴建立平面直角坐标系,如图所示.
考点突破
3
真题体验
PART THREE
解析 作出示意图如图所示.
1.(2018·全国Ⅰ)在△ABC中,AD为BC边上的中线,E为AD的中点,则
√
1
2
3
4
5
真题体验
A.-3 B.-2 C.2 D.3
√
1
2
3
4
5
真题体验
3.(2019·全国Ⅰ)已知非零向量a,b满足|a|=2|b|,且(a-b)⊥b,则a与b的夹角为
√
解析 设a与b的夹角为α,∵(a-b)⊥b,∴(a-b)·b=0,
∴a·b=b2,∴|a|·|b|cos α=|b|2,又|a|=2|b|,
1
2
3
4
5
真题体验
1
2
3
4
5
4.(2020·全国Ⅱ)已知单位向量a,b的夹角为60°,则在下列向量中,与b垂直的是
A.a+2b B.2a+b C.a-2b D.2a-b
√
真题体验
1
2
3
4
5
解析 由题意得|a|=|b|=1,
设a,b的夹角为θ=60°,
真题体验
1
2
3
4
5
5.(2020·江苏)在△ABC中,AB=4,AC=3,∠BAC=90°,D在边BC
真题体验
解析 如图,以点A为坐标原点,AB,AC所在的直线分别为x轴、y轴建立平面直角坐标系,
1
2
3
4
5
真题体验
1
2
3
4
5
真题体验
1
2
3
4
5
∴P(0,9),此时C与D重合,CD=0.
真题体验
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
