苏教版(2019)高中数学必修第二册第9章 平面向量 单元综合测试B(含解析)
文档属性
| 名称 | 苏教版(2019)高中数学必修第二册第9章 平面向量 单元综合测试B(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-10 10:14:19 | ||
图片预览




文档简介
单元综合测试B
一、选择题(本题共12小题,每小题5分,共60分)
1.设是不共线的两个向量,下列四组向量:
①;
②;
③;
④.
其中与共线的组数为( )
A.1
B.2
C.3
D.4
2.平面上有三点,设,若的长度恰好相等,则有( )
A.三点必在同一直线上
B.必为等腰三角形且为顶角
C.必为直角三角形且
D.必为等腰直角三角形
3.设为基底向量,已知向量,若三点共线,则的值是( )
A.2
B.
C.
D.3
4.向量,则( )
A.
B.0
C.1
D.2
5.已知向量,若,则锐角为( )
A.
B.
C.
D.
6.设点是所在平面内的一点,满足,则点是的( )
A.三个内角的角平分线的交点
B.三条边的垂直平分线的交点
C.三条中线的交点
D.三条高线的交点
7.已知四点的坐标分别为,4),,则此四边形的形状为( )
A.梯形
B.菱形
C.矩形
D.正方形
8.已知平面向量,且,则( )
A.
B.
C.1
D.3
9.在中,点是的中点,,点在上,且满足,则( )
A.
B.
C.
D.
10.已知向量,则的值不可能是( )
A.
B.
C.2
D.
11.已知,且,则( )
A.
B.
C.0
D.
12.已知是平面内的一定点,是平面内不共线的三个动点,若动点满足,则( )
A.动点的轨迹一定通过的重心
B.动点的轨迹一定通过的内心
C.动点的轨迹一定通过的外心
D.动点的轨迹一定通过的垂心
二、填空题(本题共4小题,每小题5分,共20分)
13.以原点和为两个顶点作等腰直角三角形,则点的坐标为______.
14.若与的夹角为,若,则的值为______.
15.已知与的夹角为,则向量在向量上的投影向量是______.
16.已知为内一点,且,则与的面积之比是______.
三、解答题(共70分)
17.(10分)已知向量,其中.
(1)求;
(2)求与的夹角的余弦值.
18.(12分)某人骑车以大小为的速度向东行驶,感到风从正北方向吹来,而当速度大小为时,感到风从东北方向吹来,试求实际风速的大小和方向.
19.(12分)已知向量.
(1)若点能构成三角形,求实数应满足的条件;
(2)若为直角三角形,且为直角,求实数的值.
20.(12分)已知向量,向量与向量的夹角为,且.
(1)求向量;
(2)设向量,向量,其中,若,试求的取值范围.
21.(12分)如图,在中,与相交于点的延长线与边交于点.
(1)用和分别表示和;
(2)如果,求实数和的值;
(3)确定点在边上的位置.
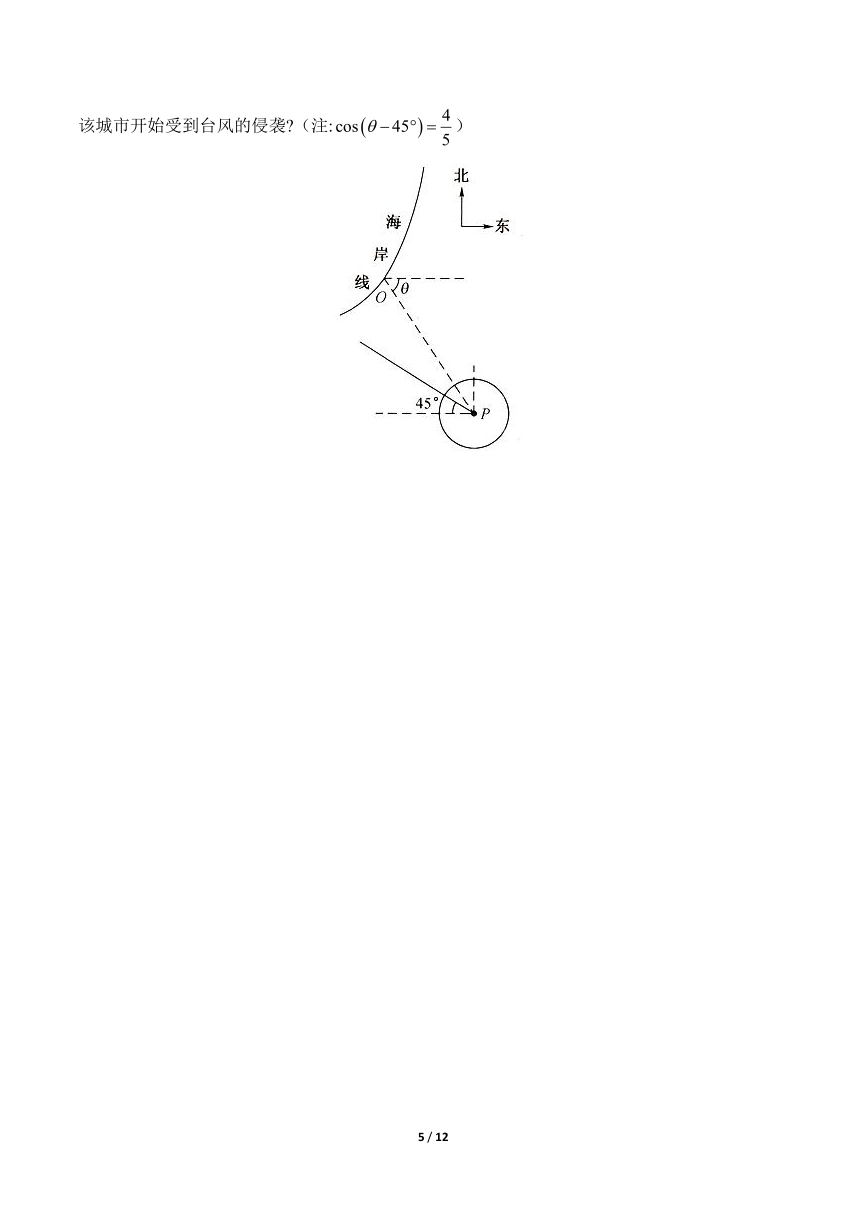
22.(12分)在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市(如图所示)的东偏南方向的海面处,并以的速度向西偏北方向移动.台风侵袭的范围为圆形区域,当前半径为,并以的速度不断增大.问几小时后该城市开始受到台风的侵袭 (注:)
参考答案
1.
答案:C
解析:①中,.③中,.④中,.
②中,不存在实数,使与不共线.
2.
答案:C
解析:∵,∴,如图所示,
即中,对角线相等,∴是矩形,且.
3.
答案:A
解析:易知,又三点共线,则,则.
4.
答案:C
解析:∵,∴
5.
答案:A
解析:∵.又∵为锐角,∴.
6.
答案:D
解析:由,得,即
∴.同理可证.∴,即点是的三条高线的交点.
7.
答案:A
解析:∵,∴共线.
又该四边形为梯形.
8.
答案:C
解析:由题意得,解得.
9.
答案:A
解析:由题意可知点是的重心,∴,
10.
答案:D
解析:由题意得.
因为,所以,
所以.结合选项可知选D.
11.
答案:B
解析:由已知得,将等式两边平方得,化简得,
同理由两边平方,得
12.
答案:D
解析:由条件,得,
从而,
所以,则动点的轨迹一定通过的垂心.
13.
答案:或
解析:设则,.∵,
∴,即.①
设的中点为,则点.
在等腰直角中,,∴,即.②
解①②得或点的坐标为或
14.
答案:
解析:由题意知,
即,解得.
15.
答案:
解析:向量在上的投影向量为.
16.
答案:
解析:如图所示,取的中点,
则为的中点,
17.
答案:见解析
解析:(1)因为,所以,,
所以,,所以.
(2)设与的夹角为,则.
18.
答案:见解析
解析:设表示此人以大小为的速度向东行驶的向量,
无风时此人感到风速为,设实际风速为,那么此时人感到的风速为,如图,
设,∵这就是感到由正北方向吹来的风速.
∵,
于是当此人的速度大小是原来的2倍时,所感受到由东北方向吹来的风速就是,
由题意得,从而,为等腰直角三角形,
∴,
设.∴实际风速是大小为的西北风.
19.
答案:见解析
解析:已知向量,
(1)若点能构成三角形,则这三点不共线,∴.
故若点能构成三角形,则实数应满足.
(2)若为直角三角形,且为直角,则,解得.
故若为直三角形,且为直角,则实数.
20.
答案:见解析
解析:(1)令,则
解得或,所以
(2)
21.
答案:见解析
解析:(1)由,可得,
.
(2)将代入中,
有,
即,
又与不共线,∴
(3)设,由知,
∴
.
∵与不共线,
∴解得
∴,即,
∴点在的三等分点且靠近点处.
22.
答案:见解析
解析:如图,设小时后,台风中心移动到处,此时城市开始受到台风的侵袭,.
,
依题意得,解得.
故后该城市开始受到台风的侵袭.
3 / 12
一、选择题(本题共12小题,每小题5分,共60分)
1.设是不共线的两个向量,下列四组向量:
①;
②;
③;
④.
其中与共线的组数为( )
A.1
B.2
C.3
D.4
2.平面上有三点,设,若的长度恰好相等,则有( )
A.三点必在同一直线上
B.必为等腰三角形且为顶角
C.必为直角三角形且
D.必为等腰直角三角形
3.设为基底向量,已知向量,若三点共线,则的值是( )
A.2
B.
C.
D.3
4.向量,则( )
A.
B.0
C.1
D.2
5.已知向量,若,则锐角为( )
A.
B.
C.
D.
6.设点是所在平面内的一点,满足,则点是的( )
A.三个内角的角平分线的交点
B.三条边的垂直平分线的交点
C.三条中线的交点
D.三条高线的交点
7.已知四点的坐标分别为,4),,则此四边形的形状为( )
A.梯形
B.菱形
C.矩形
D.正方形
8.已知平面向量,且,则( )
A.
B.
C.1
D.3
9.在中,点是的中点,,点在上,且满足,则( )
A.
B.
C.
D.
10.已知向量,则的值不可能是( )
A.
B.
C.2
D.
11.已知,且,则( )
A.
B.
C.0
D.
12.已知是平面内的一定点,是平面内不共线的三个动点,若动点满足,则( )
A.动点的轨迹一定通过的重心
B.动点的轨迹一定通过的内心
C.动点的轨迹一定通过的外心
D.动点的轨迹一定通过的垂心
二、填空题(本题共4小题,每小题5分,共20分)
13.以原点和为两个顶点作等腰直角三角形,则点的坐标为______.
14.若与的夹角为,若,则的值为______.
15.已知与的夹角为,则向量在向量上的投影向量是______.
16.已知为内一点,且,则与的面积之比是______.
三、解答题(共70分)
17.(10分)已知向量,其中.
(1)求;
(2)求与的夹角的余弦值.
18.(12分)某人骑车以大小为的速度向东行驶,感到风从正北方向吹来,而当速度大小为时,感到风从东北方向吹来,试求实际风速的大小和方向.
19.(12分)已知向量.
(1)若点能构成三角形,求实数应满足的条件;
(2)若为直角三角形,且为直角,求实数的值.
20.(12分)已知向量,向量与向量的夹角为,且.
(1)求向量;
(2)设向量,向量,其中,若,试求的取值范围.
21.(12分)如图,在中,与相交于点的延长线与边交于点.
(1)用和分别表示和;
(2)如果,求实数和的值;
(3)确定点在边上的位置.
22.(12分)在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市(如图所示)的东偏南方向的海面处,并以的速度向西偏北方向移动.台风侵袭的范围为圆形区域,当前半径为,并以的速度不断增大.问几小时后该城市开始受到台风的侵袭 (注:)
参考答案
1.
答案:C
解析:①中,.③中,.④中,.
②中,不存在实数,使与不共线.
2.
答案:C
解析:∵,∴,如图所示,
即中,对角线相等,∴是矩形,且.
3.
答案:A
解析:易知,又三点共线,则,则.
4.
答案:C
解析:∵,∴
5.
答案:A
解析:∵.又∵为锐角,∴.
6.
答案:D
解析:由,得,即
∴.同理可证.∴,即点是的三条高线的交点.
7.
答案:A
解析:∵,∴共线.
又该四边形为梯形.
8.
答案:C
解析:由题意得,解得.
9.
答案:A
解析:由题意可知点是的重心,∴,
10.
答案:D
解析:由题意得.
因为,所以,
所以.结合选项可知选D.
11.
答案:B
解析:由已知得,将等式两边平方得,化简得,
同理由两边平方,得
12.
答案:D
解析:由条件,得,
从而,
所以,则动点的轨迹一定通过的垂心.
13.
答案:或
解析:设则,.∵,
∴,即.①
设的中点为,则点.
在等腰直角中,,∴,即.②
解①②得或点的坐标为或
14.
答案:
解析:由题意知,
即,解得.
15.
答案:
解析:向量在上的投影向量为.
16.
答案:
解析:如图所示,取的中点,
则为的中点,
17.
答案:见解析
解析:(1)因为,所以,,
所以,,所以.
(2)设与的夹角为,则.
18.
答案:见解析
解析:设表示此人以大小为的速度向东行驶的向量,
无风时此人感到风速为,设实际风速为,那么此时人感到的风速为,如图,
设,∵这就是感到由正北方向吹来的风速.
∵,
于是当此人的速度大小是原来的2倍时,所感受到由东北方向吹来的风速就是,
由题意得,从而,为等腰直角三角形,
∴,
设.∴实际风速是大小为的西北风.
19.
答案:见解析
解析:已知向量,
(1)若点能构成三角形,则这三点不共线,∴.
故若点能构成三角形,则实数应满足.
(2)若为直角三角形,且为直角,则,解得.
故若为直三角形,且为直角,则实数.
20.
答案:见解析
解析:(1)令,则
解得或,所以
(2)
21.
答案:见解析
解析:(1)由,可得,
.
(2)将代入中,
有,
即,
又与不共线,∴
(3)设,由知,
∴
.
∵与不共线,
∴解得
∴,即,
∴点在的三等分点且靠近点处.
22.
答案:见解析
解析:如图,设小时后,台风中心移动到处,此时城市开始受到台风的侵袭,.
,
依题意得,解得.
故后该城市开始受到台风的侵袭.
3 / 12
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
