人教B版高中数学必修第一册2.2.4 《均值不等式及其应用》 课件(共30张PPT)
文档属性
| 名称 | 人教B版高中数学必修第一册2.2.4 《均值不等式及其应用》 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-10 10:29:56 | ||
图片预览










文档简介
(共30张PPT)
2.2.4 均值不等式及其应用
第二章 等式与不等式
2.2 不等式
学习目标
1.掌握均值不等式,
2.结合具体实例,能用均值不等式解决简单的最大值或最小值问题.
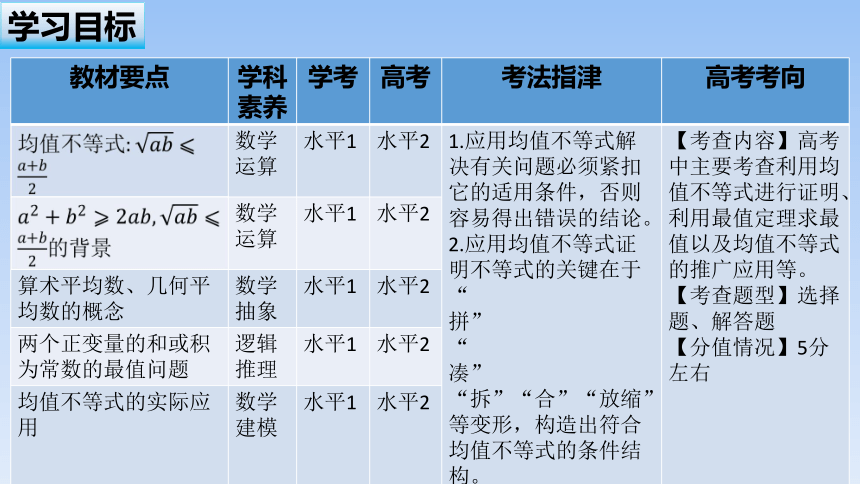
学习目标
教材要点 学科素养 学考 高考 考法指津 高考考向
均值不等式 数学运算 水平1 水平2 1.应用均值不等式解决有关问题必须紧扣它的适用条件,否则容易得出错误的结论。 2.应用均值不等式证明不等式的关键在于“拼”“凑”“拆”“合”“放缩”等变形,构造出符合均值不等式的条件结构。 【考查内容】高考中主要考查利用均值不等式进行证明、利用最值定理求最值以及均值不等式的推广应用等。
【考查题型】选择题、解答题
【分值情况】5分左右
的背景 数学运算 水平1 水平2
算术平均数、几何平均数的概念 数学抽象 水平1 水平2
两个正变量的和或积为常数的最值问题 逻辑推理 水平1 水平2
均值不等式的实际应用 数学建模 水平1 水平2
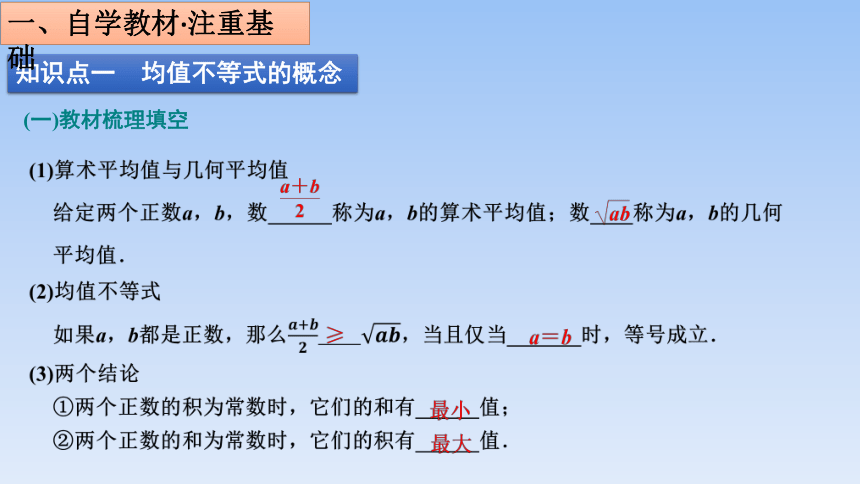
知识点一 均值不等式的概念
(一)教材梳理填空
一、自学教材·注重基础
(1)算术平均值与几何平均值
给定两个正数a,b,数______称为a,b的算术平均值;数____称为a,b的几何平均值.
(2)均值不等式
如果a,b都是正数,那么____,当且仅当_______时,等号成立.
(3)两个结论
①两个正数的积为常数时,它们的和有______值;
②两个正数的和为常数时,它们的积有______值.
(二)基本知能小试
√
×
×
一、自学教材·注重基础
知识点一 均值不等式的概念
1.判断正误
(1)对于任意a,b∈R,a2+b2≥2ab,a+b≥2 均成立. ( )
(2)若a,b同号,则≥2. ( )
(3)若a>0,b>0,则ab≤恒成立. ( )
(4)若a>0,b>0,且a≠b,则a+b>2 . ( )
√
(二)基本知能小试
一、自学教材·注重基础
知识点一 均值不等式的概念
2.设x,y满足x+y=40,且x,y都是正数,则xy的最大值是 ( )
A.400 B.100 C.40 D.20
A
解析:.
当且仅当x=y=20时,等号成立.
3.不等式(x-2y)+≥2成立的前提条件为________.
解析:因为不等式成立的前提条件是各项均为正数,所以x-2y>0,即x>2y.
(二)基本知能小试
一、自学教材·注重基础
知识点一 均值不等式的概念
4.如果a>0,那么a++2的最小值是________.
解析:因为a>0,
所以,
当且仅当a=1时等号成立.
题型一 用均值不等式证明不等式
二、提升新知·注重综合
对均值不等式的理解
(1)均值不等式成立的条件是a>0,b>0.
(2)均值不等式只有一种形式,即.都不是均值不等式.
前两个不等式可认为是均值不等式的变形式,第三个不等式是重要不等式,不是均值不等式.
证明
二、提升新知·注重综合
题型一 用均值不等式证明不等式
例1、 (1)已知x,y都是正数,求证:(x+y)(x2+y2)(x3+y3)≥8x3y3;
(2)已知a,b,c为正数,且a+b+c=1,求证:.
(1)∵x,y都是正数,
∴x+y≥2>0,
x2+y2≥2>0,x3+y3≥2>0.
∴(x+y)(x2+y2)(x3+y3)≥2 ·2 ·2 =8x3y3,
即(x+y)(x2+y2)(x3+y3)≥8x3y3,
当且仅当x=y时,等号成立.
(2)
,
当且仅当a=b=c=时,等号成立.
方法总结
二、提升新知·注重综合
题型一 用均值不等式证明不等式
利用均值不等式证明不等式的策略与注意事项
注意事项
策略
①多次使用均值不等式时,要注意等号能否成立;②对不能直接使用均值不等式的证明可重新组合,形成均值不等式模型,再使用.
从已证不等式和问题的已知条件出发,借助不等式的性质和有关定理,经过逐步的逻辑推理,最后转化为所求问题,其特征是以“已知”看“可知”,逐步推向“未知”.
变式训练
二、提升新知·注重综合
题型一 用均值不等式证明不等式
1. 已知a,b,c为不全相等的正实数,求证:.
证明:∵a>0,b>0,c>0,∴a+b≥2 >0,
,
∴ ,
即.
由于a,b,c为不全相等的正实数,故等号不成立.
∴.
变式训练
二、提升新知·注重综合
题型一 用均值不等式证明不等式
2.已知a,b,c均为正实数,且a+b+c=1.求证:.
证明:因为a,b,c均为正实数,a+b+c=1,
所以,
同理.
上述三个不等式两边均为正,分别相乘,
得.
当且仅当a=b=c=时,等号成立.
题型二 利用均值不等式求最值
二、提升新知·注重综合
利用均值不等式求最值,必须按照“一正,二定,三相等”的原则,即:
(1)一正:符合均值不等式成立的前提条件,a>0,b>0;
(2)二定:化不等式的一边为定值;
(3)三相等:必须存在取“=”号的条件,即“=”号成立.
以上三点缺一不可.
解析
二、提升新知·注重综合
题型二 利用均值不等式求最值
例2、(1)若x<0,求+3x的最大值;
(2)若x>2,求的最小值;
(3)已知,求x(1-2x)的最大值.
(1)因为x<0,
所以,
当且仅当,即x=-2时等号成立,
所以+3x的最大值为-12.
(2)因为x>2,所以,当且仅当,即x=3时等号成立,所以的最小值为4.
解析
二、提升新知·注重综合
题型二 利用均值不等式求最值
例2、(1)若x<0,求+3x的最大值;
(2)若x>2,求的最小值;
(3)已知,求x(1-2x)的最大值.
(3)因为,
所以,
当且仅当2x=1-2x,即x= 时等号成立,所以的最大值为.
方法总结
二、提升新知·注重综合
题型二 利用均值不等式求最值
均值不等式求最值的2种常用方法
常数代换法
拼凑法
常数代换法解题的关键是通过代数式的变形,构造和式或积式为定值的式子,然后利用均值不等式求解最值.应用此种方法求解最值时,应把“1”的表达式与所求最值的表达式相乘求积或相除求商
拼凑法求解最值,其实质就是先通过代数式变形拼凑出和或积为常数的两项,然后利用均值不等式求解最值.利用均值不等式求解最值时,要注意“一正、二定、三相等”,尤其是要注意验证等号成立的条件
变式训练
二、提升新知·注重综合
题型二 利用均值不等式求最值
1.[直接利用均值不等式求最值]已知x>0,y>0,且x+y=8,则(1+x)(1+y)的最大值为 ( )
A.16 B.25 C.9 D.36
B
解析:因为x>0,y>0,且x+y=8,
所以(1+x)(1+y)=1+x+y+xy=9+xy≤9+2=9+42=25,
因此当且仅当x=y=4时,(1+x)(1+y)取最大值25.
变式训练
二、提升新知·注重综合
题型二 利用均值不等式求最值
2.[利用均值不等式解决恒成立问题]已知a>0,b>0,,若不等式2a+b≥9m恒成立,则m的最大值为________.
解析:由已知,可得,当且仅当时等号成立,
∴9m≤54,即m≤6.
6
变式训练
二、提升新知·注重综合
题型二 利用均值不等式求最值
3.[借助拼凑法利用均值不等式求最值] 已知x<,则4x-2+的最大值为________.
解析:因为x< ,所以4x-5<0,则5-4x>0,
所以4x-2+ =4x-5++3.
因为,
所以.
所以.
当且仅当,即x=1时,等号成立.
故当x=1时,取最大值1.
1
变式训练
二、提升新知·注重综合
题型二 利用均值不等式求最值
4.[借助常数代换法利用均值不等式求最值]已知x>0,y>0,且,则x+y的最小值为________.
解析:∵x>0,y>0,=1,
∴x+y=()(x+y)=+10≥6+10=16,
当且仅当,又=1,即x=4,y=12时,上式取等号.
故当x=4,y=12时,x+y取得最小值16.
16
解析
二、提升新知·注重综合
题型三 利用均值不等式解应用题
例3、如图所示,用总长为定值l的篱笆围成长方形的场地,以墙为一边,并用平行于一边的篱笆隔开.
(1)设场地面积为y,垂直于墙的边长为x,试将y表示成x的表达式.
(2)怎样围才能使得场地的面积最大?最大面积是多少?
(1)设场地面积为y,垂直于墙的边长为x,
它的面积y=x(l-3x).
由x>0,且l-3x>0,可得x的范围为.
(2),
当x=时,这块长方形场地的面积最大,
这时的长为l-3x=l,最大面积为.
方法总结
二、提升新知·注重综合
题型三 利用均值不等式解应用题
求实际问题中最值的解题4步骤
(1)先读懂题意,设出变量,理清思踣,列岀函数关系式.
(2)把实际问题抽象成函数的最大值或最小值问题.
(3)在定义域内,求函数的最大值或最小值时,一般先考虑均值不等式.
(4)回到实际问题中,正确写出答案
变式训练
二、提升新知·注重综合
题型三 利用均值不等式解应用题
1.[利用均值不等式求实际问题中的最小值]将一根铁丝切割成三段做一个面积为2 m2,形状为直角三角形的框架,在下列四种长度的铁丝中,选用最合理(够用且浪费最少)的是( )
A.6.5 m B.6.8 m C.7 m D.7.2 m
C
解析:设两直角边分别为a,b,直角三角形的框架的周长为l,则
(m)(当且仅当a=b时,取等号).因为要求够用且浪费最少,故选C.
变式训练
二、提升新知·注重综合
题型三 利用均值不等式解应用题
2.[利用均值不等式求实际问题中的最大值]某公司购买一批机器投入生产,据市场分析,每台机器生产的产品可获得的总利润y(单位:万元)与机器运转时间x(单位:年)的关系为y=-x2+18x-25(x∈N*),则当每台机器运转________年时,年平均利润最大,最大值是________万元.
解析:每台机器运转x年的年平均利润为,且x>0,
故,当且仅当x=5时等号成立,
此时年平均利润最大,最大值为8万元.
5
8
变式训练
二、提升新知·注重综合
题型三 利用均值不等式解应用题
3.[利用均值不等式求实际问题中的最大值]某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场,其总面积为3 000 m2,其中场地四周(阴影部分)为通道,通道宽度均为2 m,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米.
(1)分别写出用x表示y和S的关系式;
(2)怎样设计能使S取得最大值,最大值为多少?
变式训练
二、提升新知·注重综合
题型三 利用均值不等式解应用题
解析:(1)由已知xy=3 000,2a+6=y,则y=(6<x<500),
S=(x-4)a+(x-6)a=(2x-10)a=(2x-10)
=(x-5)(y-6)=3 030-6x-(6<x<500).
(2)S=3 030-6x-≤3 030-2
=3 030-2×300=2 430.
当且仅当6x=,即x=50时,“=”成立,此时x=50,y=60,Smax=2 430.
即设计x=50 m,y=60 m时,运动场地面积最大,最大值为2 430 m2.
当堂练习
一、基础经典题
三、训练素养·注重应用、创新
1.下列不等式中,正确的是 ( )
A. B.a2+b2≥4ab
C. D.
D
解析: a<0,则不成立,故A错;a=1,b=1,a2+b2<4ab,故B错,a=4,b=16,则,故C错;由均值不等式可知D项正确.
当堂练习
一、基础经典题
三、训练素养·注重应用、创新
2.已知x<0,则有 ( )
A.最大值为0 B.最小值为0
C.最大值为-4 D.最小值为-4
C
解析:∵x<0,
,
当且仅当,即x=-1时取等号.
3.的最小值是____________.
解析:,当且仅当x2= -1时等号成立.
当堂练习
一、基础经典题
三、训练素养·注重应用、创新
4.某公司一年购买某种货物400吨,每次都购买x吨,运费为4万元/次,一年的总存储费用为4x万元,要使一年的总运费与总存储费用之和最小,则x=________吨.
解析:每年购买次数为次.
∴总费用=,
当且仅当,即x=20时等号成立.
20
当堂练习
二、创新应用题
三、训练素养·注重应用、创新
5.设a,b,c都是正数,试证明不等式:.
证明:因为a>0,b>0,c>0,
所以,
所以,
当且仅当,
即a=b=c时,等号成立.
所以.
2.2.4 均值不等式及其应用
第二章 等式与不等式
2.2 不等式
学习目标
1.掌握均值不等式,
2.结合具体实例,能用均值不等式解决简单的最大值或最小值问题.
学习目标
教材要点 学科素养 学考 高考 考法指津 高考考向
均值不等式 数学运算 水平1 水平2 1.应用均值不等式解决有关问题必须紧扣它的适用条件,否则容易得出错误的结论。 2.应用均值不等式证明不等式的关键在于“拼”“凑”“拆”“合”“放缩”等变形,构造出符合均值不等式的条件结构。 【考查内容】高考中主要考查利用均值不等式进行证明、利用最值定理求最值以及均值不等式的推广应用等。
【考查题型】选择题、解答题
【分值情况】5分左右
的背景 数学运算 水平1 水平2
算术平均数、几何平均数的概念 数学抽象 水平1 水平2
两个正变量的和或积为常数的最值问题 逻辑推理 水平1 水平2
均值不等式的实际应用 数学建模 水平1 水平2
知识点一 均值不等式的概念
(一)教材梳理填空
一、自学教材·注重基础
(1)算术平均值与几何平均值
给定两个正数a,b,数______称为a,b的算术平均值;数____称为a,b的几何平均值.
(2)均值不等式
如果a,b都是正数,那么____,当且仅当_______时,等号成立.
(3)两个结论
①两个正数的积为常数时,它们的和有______值;
②两个正数的和为常数时,它们的积有______值.
(二)基本知能小试
√
×
×
一、自学教材·注重基础
知识点一 均值不等式的概念
1.判断正误
(1)对于任意a,b∈R,a2+b2≥2ab,a+b≥2 均成立. ( )
(2)若a,b同号,则≥2. ( )
(3)若a>0,b>0,则ab≤恒成立. ( )
(4)若a>0,b>0,且a≠b,则a+b>2 . ( )
√
(二)基本知能小试
一、自学教材·注重基础
知识点一 均值不等式的概念
2.设x,y满足x+y=40,且x,y都是正数,则xy的最大值是 ( )
A.400 B.100 C.40 D.20
A
解析:.
当且仅当x=y=20时,等号成立.
3.不等式(x-2y)+≥2成立的前提条件为________.
解析:因为不等式成立的前提条件是各项均为正数,所以x-2y>0,即x>2y.
(二)基本知能小试
一、自学教材·注重基础
知识点一 均值不等式的概念
4.如果a>0,那么a++2的最小值是________.
解析:因为a>0,
所以,
当且仅当a=1时等号成立.
题型一 用均值不等式证明不等式
二、提升新知·注重综合
对均值不等式的理解
(1)均值不等式成立的条件是a>0,b>0.
(2)均值不等式只有一种形式,即.都不是均值不等式.
前两个不等式可认为是均值不等式的变形式,第三个不等式是重要不等式,不是均值不等式.
证明
二、提升新知·注重综合
题型一 用均值不等式证明不等式
例1、 (1)已知x,y都是正数,求证:(x+y)(x2+y2)(x3+y3)≥8x3y3;
(2)已知a,b,c为正数,且a+b+c=1,求证:.
(1)∵x,y都是正数,
∴x+y≥2>0,
x2+y2≥2>0,x3+y3≥2>0.
∴(x+y)(x2+y2)(x3+y3)≥2 ·2 ·2 =8x3y3,
即(x+y)(x2+y2)(x3+y3)≥8x3y3,
当且仅当x=y时,等号成立.
(2)
,
当且仅当a=b=c=时,等号成立.
方法总结
二、提升新知·注重综合
题型一 用均值不等式证明不等式
利用均值不等式证明不等式的策略与注意事项
注意事项
策略
①多次使用均值不等式时,要注意等号能否成立;②对不能直接使用均值不等式的证明可重新组合,形成均值不等式模型,再使用.
从已证不等式和问题的已知条件出发,借助不等式的性质和有关定理,经过逐步的逻辑推理,最后转化为所求问题,其特征是以“已知”看“可知”,逐步推向“未知”.
变式训练
二、提升新知·注重综合
题型一 用均值不等式证明不等式
1. 已知a,b,c为不全相等的正实数,求证:.
证明:∵a>0,b>0,c>0,∴a+b≥2 >0,
,
∴ ,
即.
由于a,b,c为不全相等的正实数,故等号不成立.
∴.
变式训练
二、提升新知·注重综合
题型一 用均值不等式证明不等式
2.已知a,b,c均为正实数,且a+b+c=1.求证:.
证明:因为a,b,c均为正实数,a+b+c=1,
所以,
同理.
上述三个不等式两边均为正,分别相乘,
得.
当且仅当a=b=c=时,等号成立.
题型二 利用均值不等式求最值
二、提升新知·注重综合
利用均值不等式求最值,必须按照“一正,二定,三相等”的原则,即:
(1)一正:符合均值不等式成立的前提条件,a>0,b>0;
(2)二定:化不等式的一边为定值;
(3)三相等:必须存在取“=”号的条件,即“=”号成立.
以上三点缺一不可.
解析
二、提升新知·注重综合
题型二 利用均值不等式求最值
例2、(1)若x<0,求+3x的最大值;
(2)若x>2,求的最小值;
(3)已知,求x(1-2x)的最大值.
(1)因为x<0,
所以,
当且仅当,即x=-2时等号成立,
所以+3x的最大值为-12.
(2)因为x>2,所以,当且仅当,即x=3时等号成立,所以的最小值为4.
解析
二、提升新知·注重综合
题型二 利用均值不等式求最值
例2、(1)若x<0,求+3x的最大值;
(2)若x>2,求的最小值;
(3)已知,求x(1-2x)的最大值.
(3)因为,
所以,
当且仅当2x=1-2x,即x= 时等号成立,所以的最大值为.
方法总结
二、提升新知·注重综合
题型二 利用均值不等式求最值
均值不等式求最值的2种常用方法
常数代换法
拼凑法
常数代换法解题的关键是通过代数式的变形,构造和式或积式为定值的式子,然后利用均值不等式求解最值.应用此种方法求解最值时,应把“1”的表达式与所求最值的表达式相乘求积或相除求商
拼凑法求解最值,其实质就是先通过代数式变形拼凑出和或积为常数的两项,然后利用均值不等式求解最值.利用均值不等式求解最值时,要注意“一正、二定、三相等”,尤其是要注意验证等号成立的条件
变式训练
二、提升新知·注重综合
题型二 利用均值不等式求最值
1.[直接利用均值不等式求最值]已知x>0,y>0,且x+y=8,则(1+x)(1+y)的最大值为 ( )
A.16 B.25 C.9 D.36
B
解析:因为x>0,y>0,且x+y=8,
所以(1+x)(1+y)=1+x+y+xy=9+xy≤9+2=9+42=25,
因此当且仅当x=y=4时,(1+x)(1+y)取最大值25.
变式训练
二、提升新知·注重综合
题型二 利用均值不等式求最值
2.[利用均值不等式解决恒成立问题]已知a>0,b>0,,若不等式2a+b≥9m恒成立,则m的最大值为________.
解析:由已知,可得,当且仅当时等号成立,
∴9m≤54,即m≤6.
6
变式训练
二、提升新知·注重综合
题型二 利用均值不等式求最值
3.[借助拼凑法利用均值不等式求最值] 已知x<,则4x-2+的最大值为________.
解析:因为x< ,所以4x-5<0,则5-4x>0,
所以4x-2+ =4x-5++3.
因为,
所以.
所以.
当且仅当,即x=1时,等号成立.
故当x=1时,取最大值1.
1
变式训练
二、提升新知·注重综合
题型二 利用均值不等式求最值
4.[借助常数代换法利用均值不等式求最值]已知x>0,y>0,且,则x+y的最小值为________.
解析:∵x>0,y>0,=1,
∴x+y=()(x+y)=+10≥6+10=16,
当且仅当,又=1,即x=4,y=12时,上式取等号.
故当x=4,y=12时,x+y取得最小值16.
16
解析
二、提升新知·注重综合
题型三 利用均值不等式解应用题
例3、如图所示,用总长为定值l的篱笆围成长方形的场地,以墙为一边,并用平行于一边的篱笆隔开.
(1)设场地面积为y,垂直于墙的边长为x,试将y表示成x的表达式.
(2)怎样围才能使得场地的面积最大?最大面积是多少?
(1)设场地面积为y,垂直于墙的边长为x,
它的面积y=x(l-3x).
由x>0,且l-3x>0,可得x的范围为.
(2),
当x=时,这块长方形场地的面积最大,
这时的长为l-3x=l,最大面积为.
方法总结
二、提升新知·注重综合
题型三 利用均值不等式解应用题
求实际问题中最值的解题4步骤
(1)先读懂题意,设出变量,理清思踣,列岀函数关系式.
(2)把实际问题抽象成函数的最大值或最小值问题.
(3)在定义域内,求函数的最大值或最小值时,一般先考虑均值不等式.
(4)回到实际问题中,正确写出答案
变式训练
二、提升新知·注重综合
题型三 利用均值不等式解应用题
1.[利用均值不等式求实际问题中的最小值]将一根铁丝切割成三段做一个面积为2 m2,形状为直角三角形的框架,在下列四种长度的铁丝中,选用最合理(够用且浪费最少)的是( )
A.6.5 m B.6.8 m C.7 m D.7.2 m
C
解析:设两直角边分别为a,b,直角三角形的框架的周长为l,则
(m)(当且仅当a=b时,取等号).因为要求够用且浪费最少,故选C.
变式训练
二、提升新知·注重综合
题型三 利用均值不等式解应用题
2.[利用均值不等式求实际问题中的最大值]某公司购买一批机器投入生产,据市场分析,每台机器生产的产品可获得的总利润y(单位:万元)与机器运转时间x(单位:年)的关系为y=-x2+18x-25(x∈N*),则当每台机器运转________年时,年平均利润最大,最大值是________万元.
解析:每台机器运转x年的年平均利润为,且x>0,
故,当且仅当x=5时等号成立,
此时年平均利润最大,最大值为8万元.
5
8
变式训练
二、提升新知·注重综合
题型三 利用均值不等式解应用题
3.[利用均值不等式求实际问题中的最大值]某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场,其总面积为3 000 m2,其中场地四周(阴影部分)为通道,通道宽度均为2 m,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米.
(1)分别写出用x表示y和S的关系式;
(2)怎样设计能使S取得最大值,最大值为多少?
变式训练
二、提升新知·注重综合
题型三 利用均值不等式解应用题
解析:(1)由已知xy=3 000,2a+6=y,则y=(6<x<500),
S=(x-4)a+(x-6)a=(2x-10)a=(2x-10)
=(x-5)(y-6)=3 030-6x-(6<x<500).
(2)S=3 030-6x-≤3 030-2
=3 030-2×300=2 430.
当且仅当6x=,即x=50时,“=”成立,此时x=50,y=60,Smax=2 430.
即设计x=50 m,y=60 m时,运动场地面积最大,最大值为2 430 m2.
当堂练习
一、基础经典题
三、训练素养·注重应用、创新
1.下列不等式中,正确的是 ( )
A. B.a2+b2≥4ab
C. D.
D
解析: a<0,则不成立,故A错;a=1,b=1,a2+b2<4ab,故B错,a=4,b=16,则,故C错;由均值不等式可知D项正确.
当堂练习
一、基础经典题
三、训练素养·注重应用、创新
2.已知x<0,则有 ( )
A.最大值为0 B.最小值为0
C.最大值为-4 D.最小值为-4
C
解析:∵x<0,
,
当且仅当,即x=-1时取等号.
3.的最小值是____________.
解析:,当且仅当x2= -1时等号成立.
当堂练习
一、基础经典题
三、训练素养·注重应用、创新
4.某公司一年购买某种货物400吨,每次都购买x吨,运费为4万元/次,一年的总存储费用为4x万元,要使一年的总运费与总存储费用之和最小,则x=________吨.
解析:每年购买次数为次.
∴总费用=,
当且仅当,即x=20时等号成立.
20
当堂练习
二、创新应用题
三、训练素养·注重应用、创新
5.设a,b,c都是正数,试证明不等式:.
证明:因为a>0,b>0,c>0,
所以,
所以,
当且仅当,
即a=b=c时,等号成立.
所以.
