24.1.4 圆周角课件
文档属性
| 名称 | 24.1.4 圆周角课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 396.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-01-05 10:50:24 | ||
图片预览


文档简介
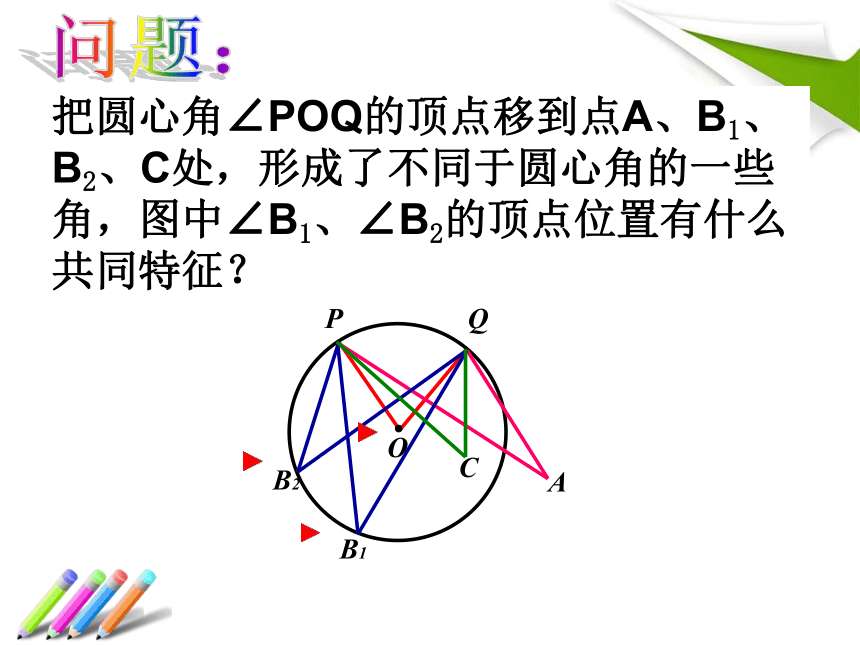
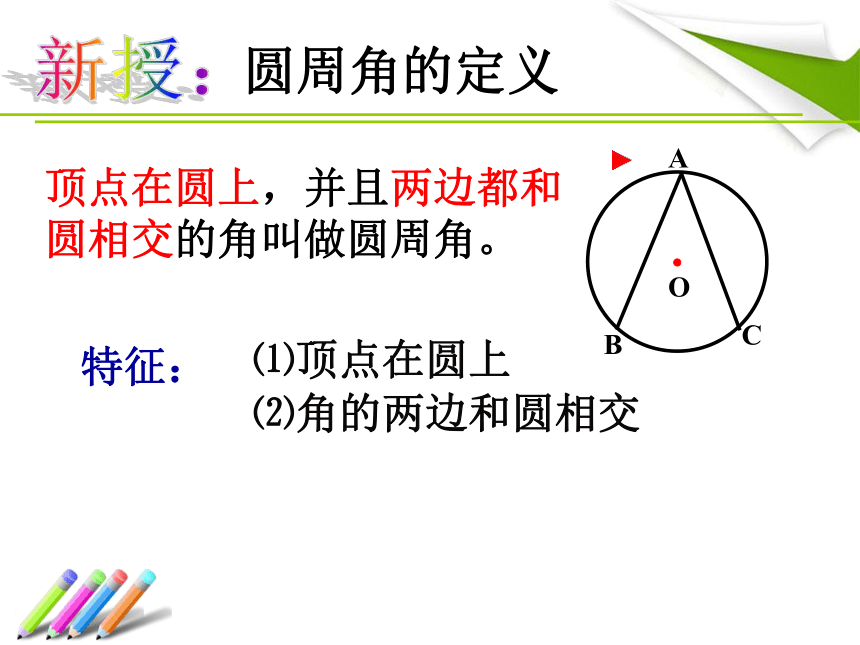
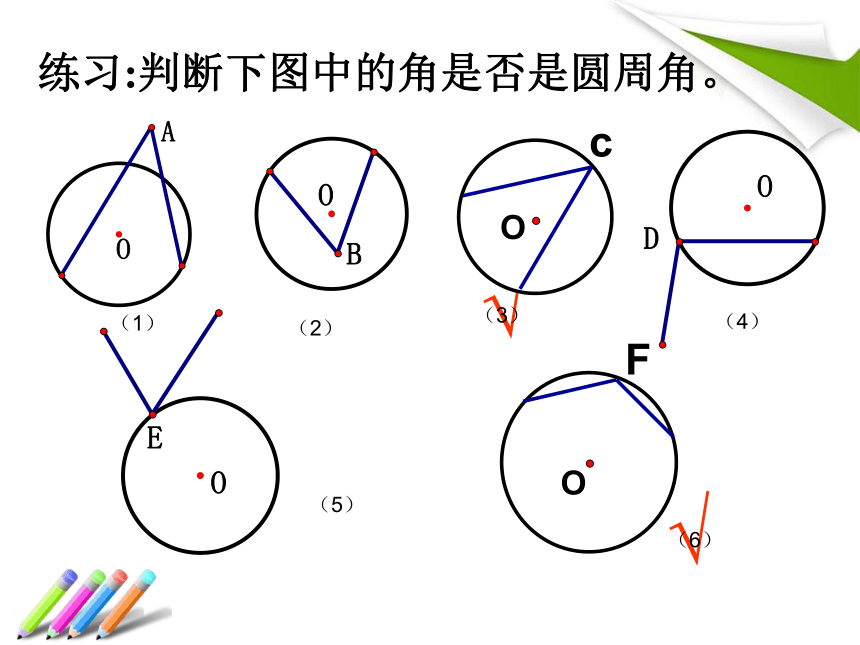
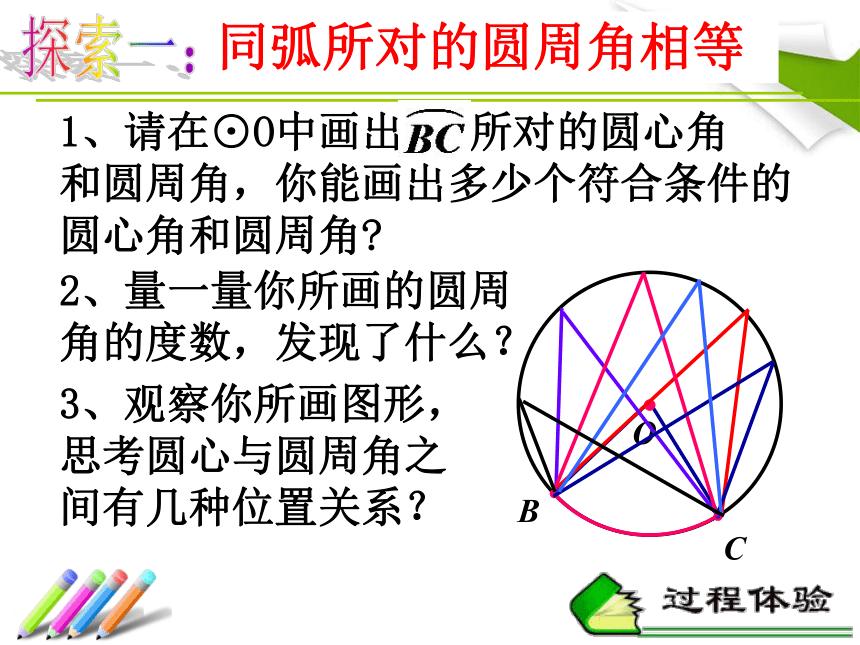
课件24张PPT。圆周角把圆心角∠POQ的顶点移到点A、B1、B2、C处,形成了不同于圆心角的一些角,图中∠B1、∠B2的顶点位置有什么共同特征?问题:圆周角的定义顶点在圆上,并且两边都和圆相交的角叫做圆周角。⑴顶点在圆上⑵角的两边和圆相交特征:新授:练习:判断下图中的角是否是圆周角。√√(1)(2)(3)(4)(5)(6)探索一:O2、量一量你所画的圆周角的度数,发现了什么? 同弧所对的圆周角相等 1、请在⊙O中画出 所对的圆心角
和圆周角,你能画出多少个符合条件的
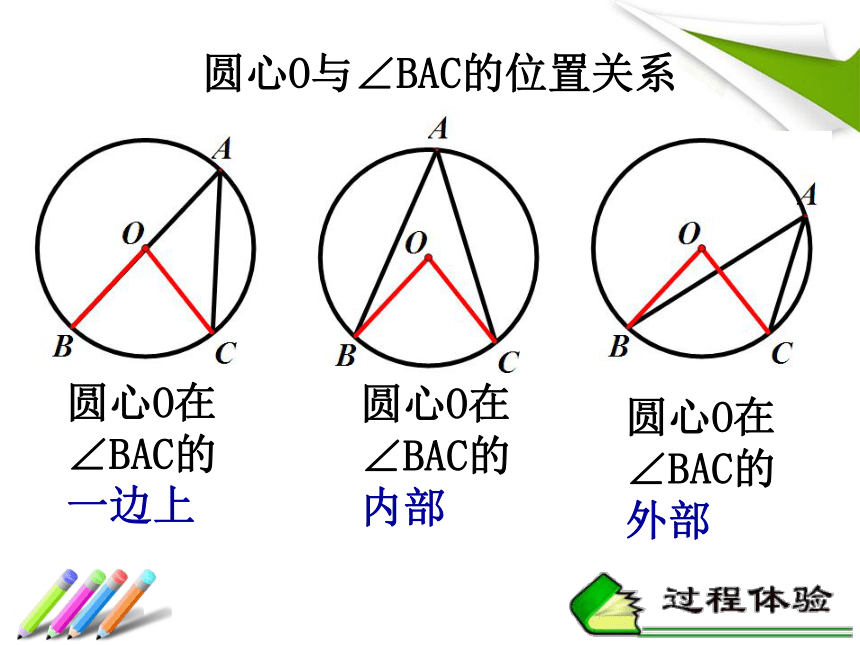
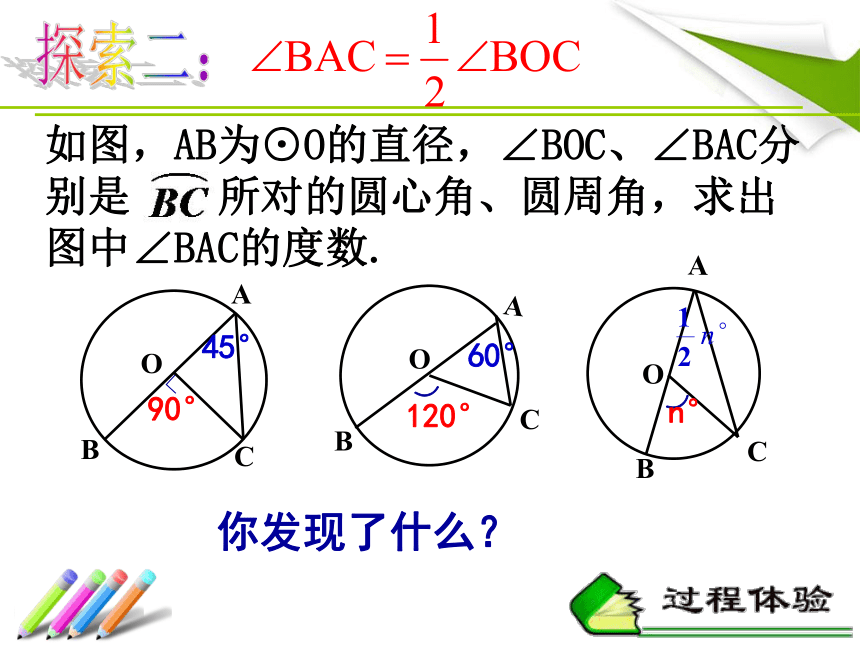
圆心角和圆周角?3、观察你所画图形,思考圆心与圆周角之间有几种位置关系?圆心与圆周角的位置关系圆心O与∠BAC的位置关系 圆心O在∠BAC的一边上圆心O在∠BAC的内部圆心O在∠BAC的外部探索二:⌒ABCn°O你发现了什么?45°60°如图,AB为⊙O的直径,∠BOC、∠BAC分别是 所对的圆心角、圆周角,求出图中∠BAC的度数.已知:⊙O中, 所对的圆周角是∠BAC,圆心角是∠BOC。
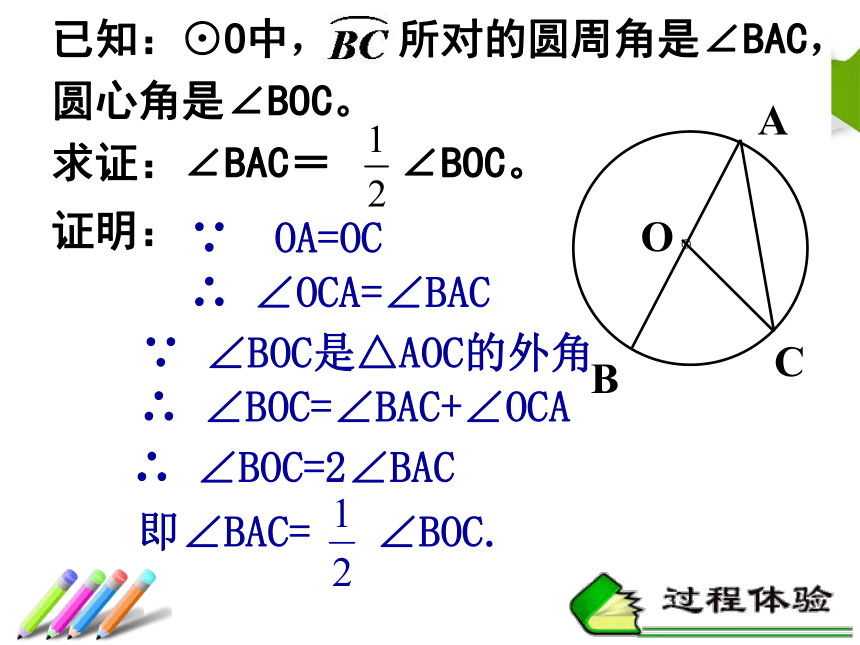
求证:∠BAC= ∠BOC。∵ OA=OC∴ ∠OCA=∠BAC证明:∵ ∠BOC是△AOC的外角∴ ∠BOC=∠BAC+∠OCA∴ ∠BOC=2∠BAC即∠BAC= ∠BOC.圆心O在∠BAC的一边上圆心O在∠BAC的内部圆心O在∠BAC的外部思考:当圆心O在∠BAC的内部或外部时,
还成立吗?圆心O在∠BAC的内部圆心O在∠BAC的外部结论:同弧所对的圆周角的度数,都等于该弧所对的圆心角的一半。 ===思考:若两条弧相等,则它们所对的圆心角有什么关系?所对的圆周角呢?同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半。圆周角定理:1、如图,点A、B、C、D在圆O上,点A与点D在点B、C所在直线的同侧,∠BAC= 35°,则(1)∠BDC= ,理由是 ;
(2)∠BOC= ,理由是 。知识应用35°70°同弧所对的圆周角相等。同弧所对的圆周角等于该弧所对的圆心角的一半。2.如图,D是弧AC的中点,与∠ABD相等的角的个数是( ).
A.4个 B.3 个 C.2 个 D.1个 BABC==知识应用观察图形,思考问题:3、如图,点A、B、C在⊙O上,点D在圆外,CD、BD分别交⊙O于点E、F,比较∠BAC与∠BDC的大小,并说明理由。CF知识应用BE思维拓展变一变:当点D在圆内时,比较∠BAC与∠BDC的大小?课堂感悟:1、圆周角2、圆周角定理⑴顶点在圆上⑵角的两边和圆相交同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.你本节课有什么收获?课堂感悟:分类由特殊到一般转化由一般到特殊谢谢
和圆周角,你能画出多少个符合条件的
圆心角和圆周角?3、观察你所画图形,思考圆心与圆周角之间有几种位置关系?圆心与圆周角的位置关系圆心O与∠BAC的位置关系 圆心O在∠BAC的一边上圆心O在∠BAC的内部圆心O在∠BAC的外部探索二:⌒ABCn°O你发现了什么?45°60°如图,AB为⊙O的直径,∠BOC、∠BAC分别是 所对的圆心角、圆周角,求出图中∠BAC的度数.已知:⊙O中, 所对的圆周角是∠BAC,圆心角是∠BOC。
求证:∠BAC= ∠BOC。∵ OA=OC∴ ∠OCA=∠BAC证明:∵ ∠BOC是△AOC的外角∴ ∠BOC=∠BAC+∠OCA∴ ∠BOC=2∠BAC即∠BAC= ∠BOC.圆心O在∠BAC的一边上圆心O在∠BAC的内部圆心O在∠BAC的外部思考:当圆心O在∠BAC的内部或外部时,
还成立吗?圆心O在∠BAC的内部圆心O在∠BAC的外部结论:同弧所对的圆周角的度数,都等于该弧所对的圆心角的一半。 ===思考:若两条弧相等,则它们所对的圆心角有什么关系?所对的圆周角呢?同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半。圆周角定理:1、如图,点A、B、C、D在圆O上,点A与点D在点B、C所在直线的同侧,∠BAC= 35°,则(1)∠BDC= ,理由是 ;
(2)∠BOC= ,理由是 。知识应用35°70°同弧所对的圆周角相等。同弧所对的圆周角等于该弧所对的圆心角的一半。2.如图,D是弧AC的中点,与∠ABD相等的角的个数是( ).
A.4个 B.3 个 C.2 个 D.1个 BABC==知识应用观察图形,思考问题:3、如图,点A、B、C在⊙O上,点D在圆外,CD、BD分别交⊙O于点E、F,比较∠BAC与∠BDC的大小,并说明理由。CF知识应用BE思维拓展变一变:当点D在圆内时,比较∠BAC与∠BDC的大小?课堂感悟:1、圆周角2、圆周角定理⑴顶点在圆上⑵角的两边和圆相交同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.你本节课有什么收获?课堂感悟:分类由特殊到一般转化由一般到特殊谢谢
同课章节目录
