苏教版五年级下册数学 圆的面积 课件 (共26张PPT)
文档属性
| 名称 | 苏教版五年级下册数学 圆的面积 课件 (共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 928.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-09 15:09:49 | ||
图片预览





文档简介
(共26张PPT)
圆 的 面 积
1.圆的( )决定圆的大小。
2.圆的周长除以它( )的商是一个固定不变的数,我们把它叫做( ),用字母( )表示。
半径
直径
圆周率
填 空
圆的面积除以( )的商,也是一个固定不变的数。
b
z
猜 想
圆的面积÷半径=?
圆的面积÷直径=?
圆的面积÷半径的平方=?
O
r
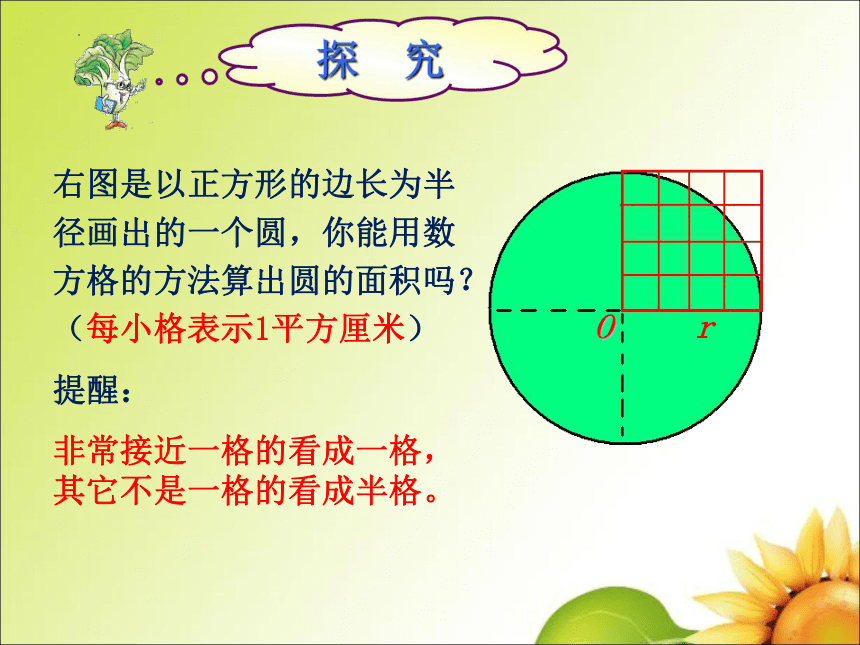
右图是以正方形的边长为半径画出的一个圆,你能用数方格的方法算出圆的面积吗?(每小格表示1平方厘米)
提醒:
非常接近一格的看成一格,其它不是一格的看成半格。
探 究
圆的直径 (厘米) 圆的半径(厘米) 正方形面积 (平方厘米) 个圆的面积 (平方厘米) 圆的面积
(平方厘米)
图1
图2
图3
8
4
16
13
52
1
2
3
4
5
6
7
8
9
10
11
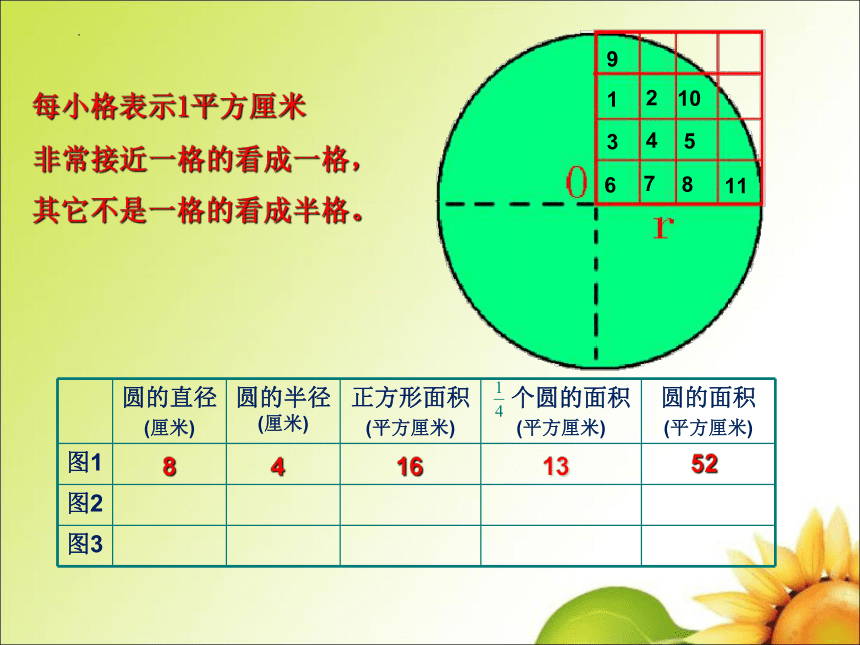
每小格表示1平方厘米
非常接近一格的看成一格,
其它不是一格的看成半格。
圆的直径 (厘米) 圆的半径 (厘米) 正方形面积 (平方厘米) 个圆的面积 (平方厘米) 圆的面积
(平方厘米)
图1
图2
图3
O
O
r
r
图2
图3
8
4
16
13
52
6
3
9
7.5
10
5
25
19.5
30
78
圆的直径 (厘米) 圆的半径(厘米) 正方形面积 (平方厘米) 个圆的面积 (平方厘米) 圆的面积
(平方厘米)
图1
图2
图3
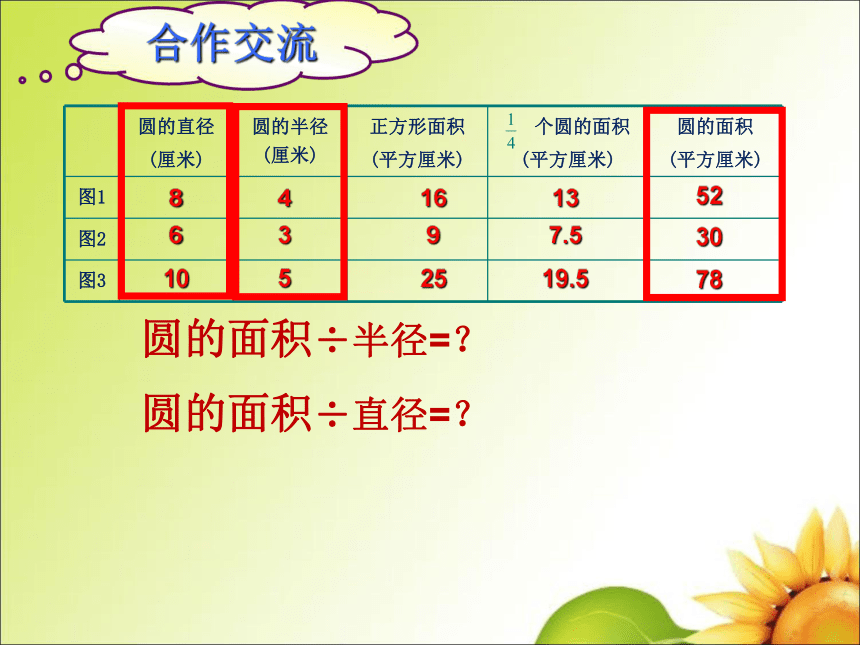
圆的面积÷半径=?
圆的面积÷直径=?
8
4
16
13
6
3
9
7.5
10
5
25
19.5
52
30
78
合作交流
圆的直径 (厘米) 圆的半径(厘米) 正方形面积 (平方厘米) 个圆的面积 (平方厘米) 圆的面积
(平方厘米)
图1
图2
图3
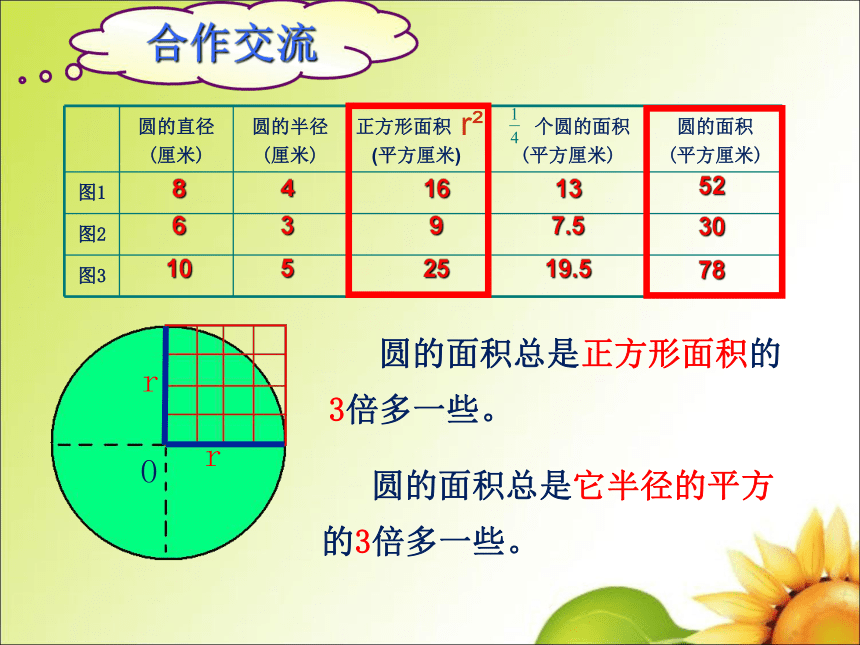
8
4
16
13
6
3
9
7.5
10
5
25
19.5
52
30
78
合作交流
O
r
圆的面积总是正方形面积的 3倍多一些。
圆的面积总是它半径的平方的3倍多一些。
r
r
疑问一:
它是一个固定不变的数吗?
疑问二:
是圆周率吗?
圆的面积÷半径的平方=
大约1700年前,我国的数学家刘徽用“割圆术”来求圆周长的近似值。他从内接正六边形算起,逐渐把边数加倍,正十二边形、正二十四边形……计算得出圆周率是3.14。并指出,内接正多边形的边数越多,周长越接近圆的周长。
……
60°
h
a
三角形的面积
正六边形的面积
S=ah÷2
S=ah÷2×6
S= h÷2
6a
6a
正六边形的周长
o
S= × h÷2
45°
h
三角形的面积怎样计算?
正八边形的面积
S=ah÷2
S=ah÷2×8
S= h÷2
8a
8a
S= × h÷2
正八边形的周长
a
正六边形的面积
S= h÷2
6a
正八边形的面积
S= h÷2
8a
S= ×h÷2
正六边形周长
S= ×h÷2
正八边形周长
正十边形的面积
正十二边形的面积
S= ×h÷2
正十边形周长
S= ×h÷2
正十二边形周长
正十边形的面积
正十二边形的面积
S= ×h÷2
正十边形周长
S= ×h÷2
正十二边形周长
S= ×h÷2
正六边形周长
S= ×h÷2
正八边形周长
正六边形的面积
正八边形的面积
正多边形的边数越来越多,正多边形就越来越接近……
h
O
……
r
圆的面积
h
O
r
正多边形周长
正多边形面积
=
×
h
÷2
圆的周长
=
×
÷2
正多边形的边数越来越多,正多边形就越来越接近圆。
S
C
H
= 2
r
r
×
÷2
S =
r2
r
r
×
=
疑问一:
它是一个固定不变的数吗?
疑问二:
是圆周率吗?
圆的面积÷半径的平方=?
S =
r2
S ÷r2 =
一个自动旋转喷水器最大喷水距离大约是5米。它旋转一周后喷灌的面积约有多少平方米?
5m
o
一个自动旋转喷水器最大喷水距离大约是5米。它旋转一周后喷灌的面积约有多少平方米?
3.14× 5
=3.14×25
=78.5(m )
S = ×5
= ×25
=25
一个自动旋转喷水器最大喷水距离大约是5米。它旋转一周后喷灌的面积约有多少平方米?
计算下面各圆的面积
3cm
8m
o
o
3cm
o
3.14×3
=3.14×9
=28.26(cm )
S= ×3
= ×9
= 9
8m
o
3.14×(8÷2)
=3.14×16
=50.24(m )
S= ×(8÷2)
= ×16
=16
我的收获
圆 的 面 积
1.圆的( )决定圆的大小。
2.圆的周长除以它( )的商是一个固定不变的数,我们把它叫做( ),用字母( )表示。
半径
直径
圆周率
填 空
圆的面积除以( )的商,也是一个固定不变的数。
b
z
猜 想
圆的面积÷半径=?
圆的面积÷直径=?
圆的面积÷半径的平方=?
O
r
右图是以正方形的边长为半径画出的一个圆,你能用数方格的方法算出圆的面积吗?(每小格表示1平方厘米)
提醒:
非常接近一格的看成一格,其它不是一格的看成半格。
探 究
圆的直径 (厘米) 圆的半径(厘米) 正方形面积 (平方厘米) 个圆的面积 (平方厘米) 圆的面积
(平方厘米)
图1
图2
图3
8
4
16
13
52
1
2
3
4
5
6
7
8
9
10
11
每小格表示1平方厘米
非常接近一格的看成一格,
其它不是一格的看成半格。
圆的直径 (厘米) 圆的半径 (厘米) 正方形面积 (平方厘米) 个圆的面积 (平方厘米) 圆的面积
(平方厘米)
图1
图2
图3
O
O
r
r
图2
图3
8
4
16
13
52
6
3
9
7.5
10
5
25
19.5
30
78
圆的直径 (厘米) 圆的半径(厘米) 正方形面积 (平方厘米) 个圆的面积 (平方厘米) 圆的面积
(平方厘米)
图1
图2
图3
圆的面积÷半径=?
圆的面积÷直径=?
8
4
16
13
6
3
9
7.5
10
5
25
19.5
52
30
78
合作交流
圆的直径 (厘米) 圆的半径(厘米) 正方形面积 (平方厘米) 个圆的面积 (平方厘米) 圆的面积
(平方厘米)
图1
图2
图3
8
4
16
13
6
3
9
7.5
10
5
25
19.5
52
30
78
合作交流
O
r
圆的面积总是正方形面积的 3倍多一些。
圆的面积总是它半径的平方的3倍多一些。
r
r
疑问一:
它是一个固定不变的数吗?
疑问二:
是圆周率吗?
圆的面积÷半径的平方=
大约1700年前,我国的数学家刘徽用“割圆术”来求圆周长的近似值。他从内接正六边形算起,逐渐把边数加倍,正十二边形、正二十四边形……计算得出圆周率是3.14。并指出,内接正多边形的边数越多,周长越接近圆的周长。
……
60°
h
a
三角形的面积
正六边形的面积
S=ah÷2
S=ah÷2×6
S= h÷2
6a
6a
正六边形的周长
o
S= × h÷2
45°
h
三角形的面积怎样计算?
正八边形的面积
S=ah÷2
S=ah÷2×8
S= h÷2
8a
8a
S= × h÷2
正八边形的周长
a
正六边形的面积
S= h÷2
6a
正八边形的面积
S= h÷2
8a
S= ×h÷2
正六边形周长
S= ×h÷2
正八边形周长
正十边形的面积
正十二边形的面积
S= ×h÷2
正十边形周长
S= ×h÷2
正十二边形周长
正十边形的面积
正十二边形的面积
S= ×h÷2
正十边形周长
S= ×h÷2
正十二边形周长
S= ×h÷2
正六边形周长
S= ×h÷2
正八边形周长
正六边形的面积
正八边形的面积
正多边形的边数越来越多,正多边形就越来越接近……
h
O
……
r
圆的面积
h
O
r
正多边形周长
正多边形面积
=
×
h
÷2
圆的周长
=
×
÷2
正多边形的边数越来越多,正多边形就越来越接近圆。
S
C
H
= 2
r
r
×
÷2
S =
r2
r
r
×
=
疑问一:
它是一个固定不变的数吗?
疑问二:
是圆周率吗?
圆的面积÷半径的平方=?
S =
r2
S ÷r2 =
一个自动旋转喷水器最大喷水距离大约是5米。它旋转一周后喷灌的面积约有多少平方米?
5m
o
一个自动旋转喷水器最大喷水距离大约是5米。它旋转一周后喷灌的面积约有多少平方米?
3.14× 5
=3.14×25
=78.5(m )
S = ×5
= ×25
=25
一个自动旋转喷水器最大喷水距离大约是5米。它旋转一周后喷灌的面积约有多少平方米?
计算下面各圆的面积
3cm
8m
o
o
3cm
o
3.14×3
=3.14×9
=28.26(cm )
S= ×3
= ×9
= 9
8m
o
3.14×(8÷2)
=3.14×16
=50.24(m )
S= ×(8÷2)
= ×16
=16
我的收获
