八年级数学第15章轴对称图形与等腰三角形期末复习课件
文档属性
| 名称 | 八年级数学第15章轴对称图形与等腰三角形期末复习课件 |  | |
| 格式 | zip | ||
| 文件大小 | 345.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-01-05 11:14:47 | ||
图片预览



文档简介
课件28张PPT。八年级数学期末复习课件
第15章 轴对称图形与等腰三角形
(复习题教材P149-153)沪科版八年级数学第15章轴对称图形与等腰三角形复习题1.已知:点A(a,b)与点B(c,d).
(1)如果点A,B关于y轴对称,那么a,b,c,d应满足什么条件?
(2)如果点A,B关于x轴对称,那么a,b,c,d应满足什么条件?答:(1)a=-c,b=d.
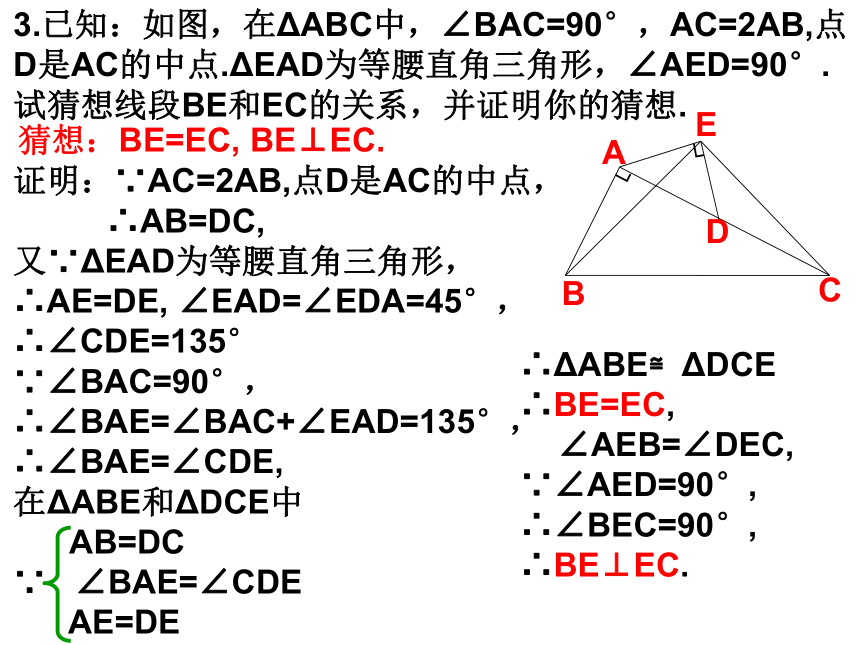
(2)a=c,b=-d.2.直线 与直线y=2x关于y轴对称,写出直线 所表示的函数表达式.答:y=-2x3.已知:如图,在ΔABC中,∠BAC=90°,AC=2AB,点
D是AC的中点.ΔEAD为等腰直角三角形,∠AED=90°.试猜想线段BE和EC的关系,并证明你的猜想.┐┐CBDAE猜想:BE=EC, BE⊥EC.证明:∵AC=2AB,点D是AC的中点,
∴AB=DC,
又∵ΔEAD为等腰直角三角形,
∴AE=DE, ∠EAD=∠EDA=45°,
∴∠CDE=135°
∵∠BAC=90°,
∴∠BAE=∠BAC+∠EAD=135°,
∴∠BAE=∠CDE,
在ΔABE和ΔDCE中
AB=DC
∵ ∠BAE=∠CDE
AE=DE
∴ΔABE≌ΔDCE
∴BE=EC,
∠AEB=∠DEC,
∵∠AED=90°,
∴∠BEC=90°,
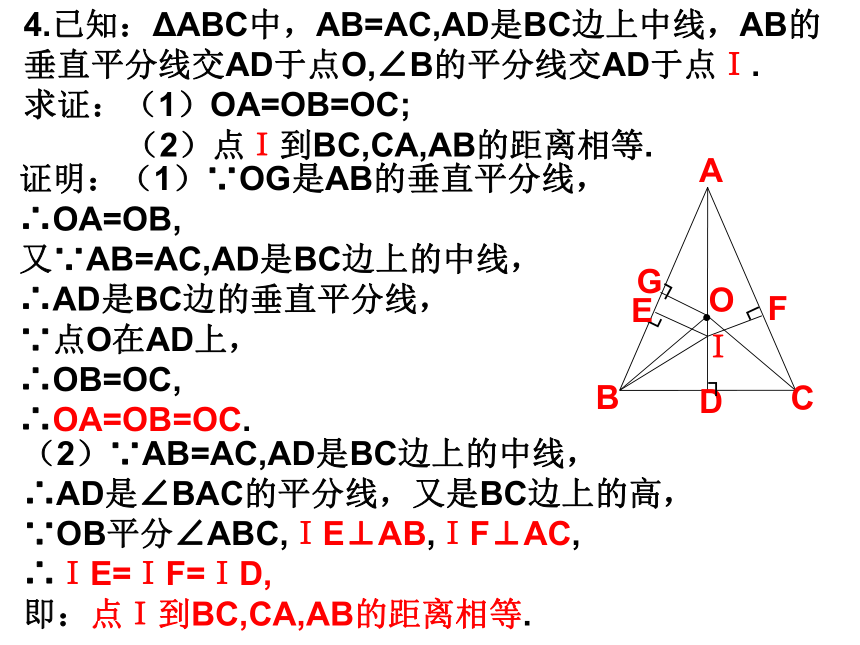
∴BE⊥EC.4.已知:ΔABC中,AB=AC,AD是BC边上中线,AB的垂直平分线交AD于点O,∠B的平分线交AD于点I.
求证:(1)OA=OB=OC;
(2)点I到BC,CA,AB的距离相等.?ODCBAI┐┐┐┐EGF证明:(1)∵OG是AB的垂直平分线,
∴OA=OB,
又∵AB=AC,AD是BC边上的中线,
∴AD是BC边的垂直平分线,
∵点O在AD上,
∴OB=OC,
∴OA=OB=OC.(2)∵AB=AC,AD是BC边上的中线,
∴AD是∠BAC的平分线,又是BC边上的高,
∵OB平分∠ABC,IE⊥AB,IF⊥AC,
∴IE=IF=ID,
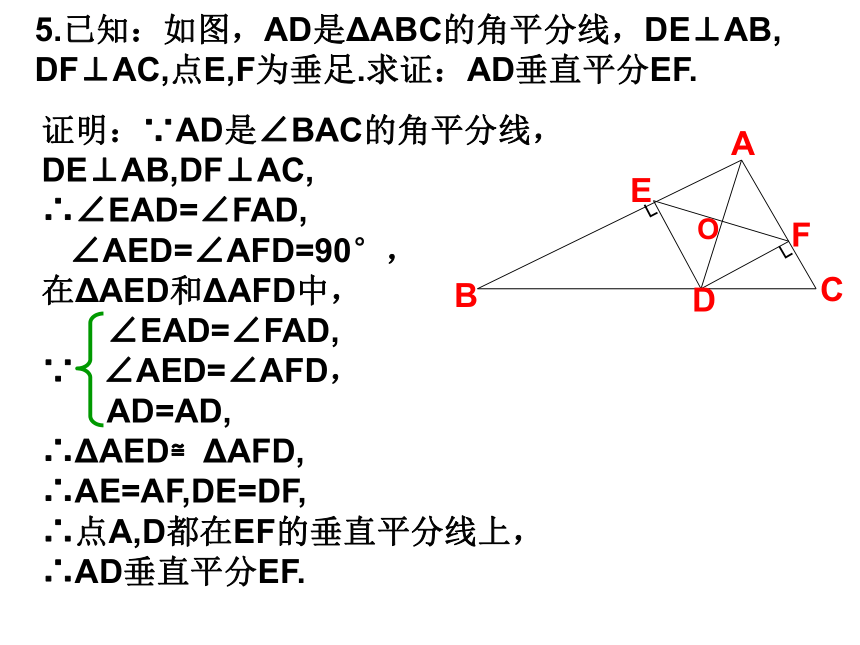
即:点I到BC,CA,AB的距离相等.5.已知:如图,AD是ΔABC的角平分线,DE⊥AB,
DF⊥AC,点E,F为垂足.求证:AD垂直平分EF.BCDFEA┐┐证明:∵AD是∠BAC的角平分线, DE⊥AB,DF⊥AC,
∴∠EAD=∠FAD,
∠AED=∠AFD=90°,
在ΔAED和ΔAFD中,
∠EAD=∠FAD,
∵ ∠AED=∠AFD,
AD=AD,
∴ΔAED≌ΔAFD,
∴AE=AF,DE=DF,
∴点A,D都在EF的垂直平分线上,
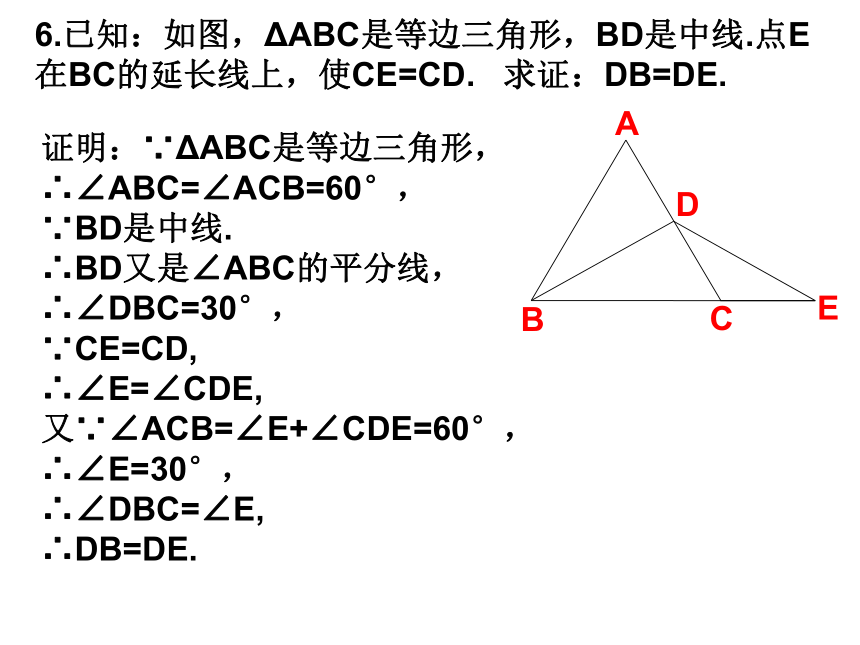
∴AD垂直平分EF.O6.已知:如图,ΔABC是等边三角形,BD是中线.点E在BC的延长线上,使CE=CD. 求证:DB=DE.ECBDA证明:∵ΔABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵BD是中线.
∴BD又是∠ABC的平分线,
∴∠DBC=30°,
∵CE=CD,
∴∠E=∠CDE,
又∵∠ACB=∠E+∠CDE=60°,
∴∠E=30°,
∴∠DBC=∠E,
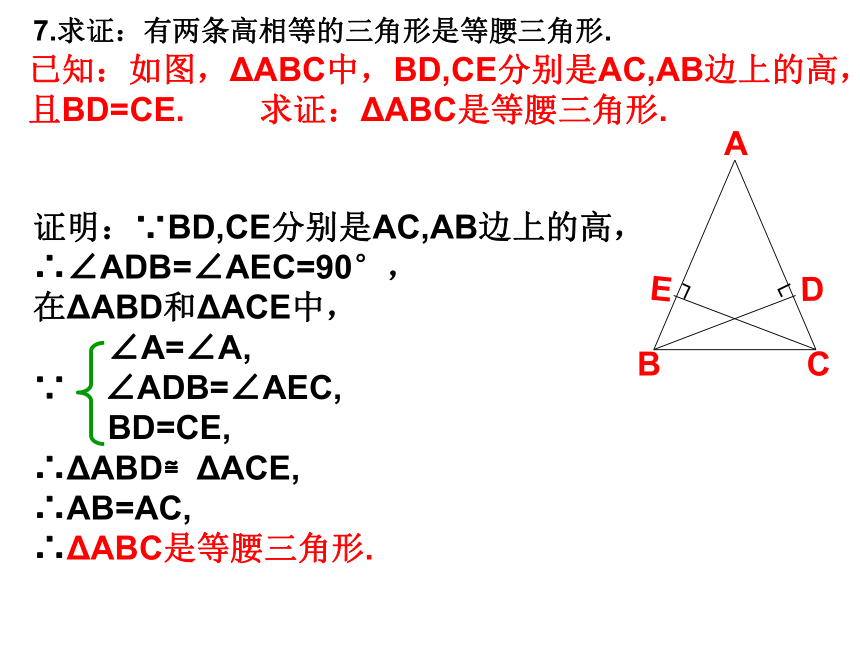
∴DB=DE.7.求证:有两条高相等的三角形是等腰三角形.已知:如图,ΔABC中,BD,CE分别是AC,AB边上的高,且BD=CE. 求证:ΔABC是等腰三角形.DECBA┐┐证明:∵BD,CE分别是AC,AB边上的高,
∴∠ADB=∠AEC=90°,
在ΔABD和ΔACE中,
∠A=∠A,
∵ ∠ADB=∠AEC,
BD=CE,
∴ΔABD≌ΔACE,
∴AB=AC,
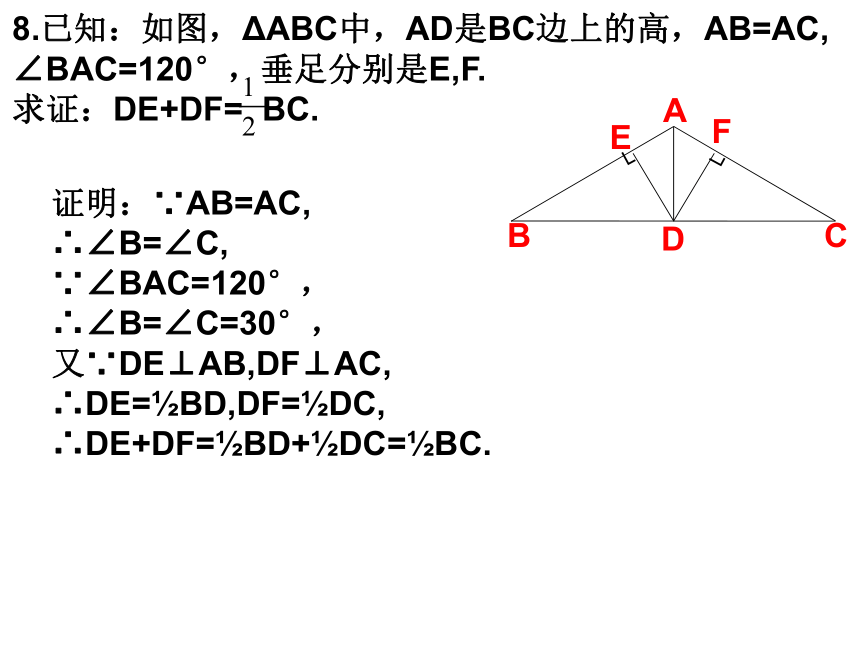
∴ΔABC是等腰三角形.8.已知:如图,ΔABC中,AD是BC边上的高,AB=AC,
∠BAC=120°,垂足分别是E,F.
求证:DE+DF= BC.┐┐FEBCDA证明:∵AB=AC,
∴∠B=∠C,
∵∠BAC=120°,
∴∠B=∠C=30°,
又∵DE⊥AB,DF⊥AC,
∴DE=?BD,DF=?DC,
∴DE+DF=?BD+?DC=?BC. 9.已知:如图,在ΔABC中,AB=AC,∠A=120°,AC的垂直平分线EF交AC于点E,交BC于点F.
求证:BF=2CF.┐FEBCA证明:连接AF,
∵AB=AC,
∴∠B=∠C,
∵∠A=120°,
∴∠B=∠C=30°,
∵EF是AC的垂直平分线,
∴AF=CF,
∴∠FAC=∠C=30°,
∴∠BAF=90°,
∴BF=2AF,
∴BF=2CF.10.已知:如图,AD⊥DE,BE⊥DE,AC,BC分别平分∠DAB,∠ABE,点C在线段DE上.求证:AB=AD+BE.DBECA┐┐F┐证明:过C作CF⊥AB,垂足为F,
又∵⊥AD,CE⊥BE,
AC平分∠DAB,BC平分∠ABE,
∴CD=CF=CE,
在RtΔACD和RtΔACF中,
AC=AC,
CD=CF,
∴RtΔACD≌RtΔACF,
∴AF=AD,
在RtΔBCE和RtΔBCF中,
BC=BC,
CE=CF,
∴RtΔBCE≌RtΔBCF,
∴BF=BE,
∴AB=AF+BF=AD+BE.11.已知:如图,在ΔABC中,∠A=90°,AB=AC,点D在BC上,BD=AB,作DE⊥BC,点E在边AC上.
求证:(1)BE平分∠ABC;(2)AE=ED=DC.CDEAB┐┐证明:(1)在RtΔABE和RtΔDBE中,
BE=BE,
AB=DB,
∴RtΔABE≌RtΔDBE,
∴∠ABE=∠DBE,
∴BE平分∠ABC;
(2)∵∠A=90°,AB=AC,
∴∠C=45°,
又∵DE⊥BC,
∴∠DEC=∠C=45°,
∴ED=DC,
∵RtΔABE≌RtΔDBE,∴AE=ED,
∴AE=ED=DC.12.已知:如图,在ΔABC中,以它的边AB,AC为边,分别在形外作等边三角形ABD,ACE,连接BE,DC.
求证:BE=DC.EDCBA证明:∵ΔABD和ΔACE都是等边三角形,
∴AB=AD,AE=AC,
∠BAD=∠CAE=60°,
∴∠BAE=∠DAC,
在ΔABE和ΔADC中,
AB=AD,
∵ ∠BAE=∠DAC,
AE=AC,
∴ΔABE≌ΔADC,
∴BE=DC.13.已知:如图,线段CD与∠AOB,通过作图求一点P,使PC=PD,并且点P到∠AOB两边的距离相等.OBDCA?14.已知:如图,RtΔABC中,∠C=90°,沿过点B的一条直线BE折叠这个三角形,使点C与边AB上的点D重合.要使D恰好为AB的中点,问还需增加一个什么条件?说明你增加的条件及依据.ABDEC可以增加:∠A=30°或BC=?AB,
或∠ABC=60°,或∠ABC=2∠A.理由:∵∠C=90°,∠A=30°,
∴BC=?AB,
由折叠可知BC=BD=?AB,
∴D为AB的中点.1.根据下列点的坐标的变化,判断它们进行了怎样的变换?
(1) (-3,-1) ( 3,-1);
(2) (-5, 6) (-5, 1);
(3) ( 4, 3) ( 4,-3);
(4) ( 2, -3) ( 3,-2).B组复习题答;:(1)关于y轴对称(或沿x轴方向向右平移6个单位).
(2)沿y轴方向向下平移5个单位(或关于直线y=3.5x对称).
(3)关于x轴对称(或沿y轴方向向下平移6个单位).
(4)关于直线y=-x对称(或先沿x轴方向向右平移1个单位,再沿y轴方向向上平移1个单位).2. BD是ΔABC的角平分线,BD的垂直平分线交CA的延长线于点E.求证:∠EAB=∠EBC.EDCBA┐证明:∵E在BD的垂直平分线上,
∴EB=ED,
∴∠EBD=∠EDB,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
又∵∠EAB=∠EDB+∠ABD,
∠EBC=∠EBD+∠DBC,
∴∠EAB=∠EBC3.已知:O是线段AB的中点,直线MN经过点O,点C,D在直线MN上,∠1=∠2=45°.
(1)若点C与点O重合[图(1)],请直接写出AC与BD的数量关系和位置关系;
(2)若点C,D不重合[图(2)],求证:AC=BD,AC⊥BD.CONANMDO(C)BAMDB211⌒⌒2⌒⌒(1)AC=BD,
AC⊥BD.3.已知:O是线段AB的中点,直线MN经过点O,点C,D在直线MN上,∠1=∠2=45°.
(2)若点C,D不重合[图(2)],求证:AC=BD,AC⊥BD.CONAMDB21⌒⌒E证明:过B作BE//AC,交MN于点E,
∴∠A=∠OBE,
又∵O是线段AB的中点,
∴OA=OB,
在ΔOAC和ΔOBE中,
∠A=∠OBE,
∵ ∠AOC=∠BOE,
OA=OB,
∴ΔOAC≌ΔOBE,
∴AC=BE,∠OCA=∠OEB,
∴∠1=∠BED
∴∠BED=∠2∵∠1=∠2=45°,
∴∠2=∠BED=45°,
∴BE=BD,∠DBE=90°,
∴AC=BD,BE⊥BD
∵BE//AC,
∴AC⊥BD4.已知:如图,在ΔABC中,∠ACB=90°,D,E是边AB上的两点,且AD=AC,BE=BC. 求证:∠DCE=45°.ACEDB证明:∵AD=AC,BE=BC,
∴∠ACD=∠ADC,∠BEC=∠BCE,
又∵∠A+∠ACD+∠ADC=180°,
∠B+∠BEC+∠BCE=180°,
∴∠A+2∠ACD=180°,∠B+2∠BCE=180°,
∴∠A+∠B+2∠ACD+2∠BCE=360°,
∴∠A+∠B+2∠ACD+2∠BCD+2∠DCE=360°,
∴∠A+∠B+2∠ACB+2∠DCE=360°,
又∵∠ACB=90°,∠A+∠B+∠ACB=180°,
∴2∠DCE=90°,
∴∠DCE=45°.5.已知:如图,点D在等边三角形ABC的边AC上,点E在边AB的延长线上,使BE=CD,DE交BC于点P.
求证:PD=PE.ABEPDCF证明:过D作DF//AB交BC于F,
∴∠CDF=∠A,∠CFD=∠CBA,
∠FDP=∠E,
又∵ΔABC是等边三角形,
∴∠A=∠CBA=∠C=60°,
∴∠C=∠CDF=∠CFD,
∴ΔCDF是等边三角形,
∴CD=FD,
∵BE=CD,
∴FD=BE,在ΔFDP和ΔBEP中,
∠FDP=∠E,
∵ ∠DPF=∠EPB,
FD=BE,
∴ΔFDP≌ΔBEP,
∴PD=PE.6.(1)已知:如图(1),在ΔABC中,∠ABC,∠ACB
的平分线交于点O,过点O的直线DE//BC,DE分别与AB,
AC交于点D,E.求证:BD+CE=DE.CBEODA(1)证明:∵DE//BC,
∴∠DOB=∠OBC,∠EOC=∠OCB,
又∵OB平分∠ABC,OC平分∠ACB,
∴∠OBD=∠OBC,∠OCE=∠OCB,
∴∠DOB=∠OBD,∠EOC=∠OCE,
∴BD=DO,CE=OE,
∴BD+CE=DO+OE,
∴BD+CE=DE.(2)将(1)题条件“∠ACB的平分线”改为“∠ACB
的外角平分线”,如图(2)所示.原来的关系式BD+CE
=DE还成立吗?如果不成立,你能推断出BD,CE,DE存
在的数量关系式吗?请证明你的推断.CBOEDA答:不成立.
BD-CE=DE.
证明:∵DE//BC,
∴∠DOB=∠OBC,∠EOC=∠OCF,
∵OB平分∠ABC,OC平分∠ACF,
∴∠OBD=∠OBC,∠OCE=∠OCF,
∴∠DOB=∠OBD,∠EOC=∠OCE,
∴BD=DO,CE=OE,
∴BD-CE=DO-OE,
∴BD-CE=DE.FC组复习题1.已知:等腰三角形ABC中,AB=AC.
(1)P为底边BC上任一点,自点P向两腰作垂线PE,PF,点E,F为垂足.求证:PE+PF等于定值;
(2)若点P在底边BC延长线上时,情况如何?FEPBAC┐┐证明:连接AP,设腰上的高为h1,
由SΔABC=SΔPAB+SΔPAC,得
?AB?PE+?AC?PF=?AB?h1.
又∵AB=AC,
∴ PE+PF=h1.
故,PE+PF等于定值.1.已知:等腰三角形ABC中,AB=AC.
(1)P为底边BC上任一点,自点P向两腰作垂线PE,PF,
点E,F为垂足.求证:PE+PF等于定值;
(2)若点P在底边BC延长线上时,情况如何?FEPCBA┐┐证明:连接AP,设腰上的高为h1,
由SΔABC=SΔPAB-SΔPAC,得
?AB?PE-?AC?PF=?AB?h1.
又∵AB=AC,
∴ PE-PF=h1.
故,PE-PF等于定值.如果,点P在底边CB延长线上时,有PF-PE=h1.2.已知:等边三角形ABC.
(1)P为ΔABC内任一点,自点P向三边作垂线PD,PE,
PF,点D,E,F为垂足.求证:PD+PE+PF等于定值;
(2)若点P在ΔABC外时,情况如何?PDFECBA┐┐┐证明:连接PA,PB,PC,
设等边ΔABC的高为h,
由SΔABC=SΔPAB+SΔPBC+SΔPAC,得
?AB?PD+?BC?PE+?AC?PF=?BC?h.
又∵AB=BC=AC,
∴PD+PE+PF=h,
故:PD+PE+PF等于定值.EDFPCBA┐┐┐当P在BA与CA的延长线所围成的区域内时,
证明:连接PA,PB,PC,
设等边ΔABC的高为h,
由SΔABC=SΔPBC-SΔPAB-SΔPAC,得
?BC?PE-?AB?PD-?AC?PF=?BC?h.
又∵AB=BC=AC,
∴PE-PD-PF=h,FEDPCBA┐┐┐当P在BA与BC的延长线所围成的区域内时,
证明:连接PA,PB,PC,
设等边ΔABC的高为h,
由SΔABC=SΔPBC+SΔPAB-SΔPAC,得
?BC?PE+?AB?PD-?AC?PF=?BC?h.
又∵AB=BC=AC,
∴PE+PD-PF=h,当P在AC与BC的延长线所围成的区域内时,
当P在AB与AC的延长线所围成的区域内时,
当P在AB与CB的延长线所围成的区域内时,
当P在CB与CA的延长线所围成的区域内时,
可以用类似的方法计算.
第15章 轴对称图形与等腰三角形
(复习题教材P149-153)沪科版八年级数学第15章轴对称图形与等腰三角形复习题1.已知:点A(a,b)与点B(c,d).
(1)如果点A,B关于y轴对称,那么a,b,c,d应满足什么条件?
(2)如果点A,B关于x轴对称,那么a,b,c,d应满足什么条件?答:(1)a=-c,b=d.
(2)a=c,b=-d.2.直线 与直线y=2x关于y轴对称,写出直线 所表示的函数表达式.答:y=-2x3.已知:如图,在ΔABC中,∠BAC=90°,AC=2AB,点
D是AC的中点.ΔEAD为等腰直角三角形,∠AED=90°.试猜想线段BE和EC的关系,并证明你的猜想.┐┐CBDAE猜想:BE=EC, BE⊥EC.证明:∵AC=2AB,点D是AC的中点,
∴AB=DC,
又∵ΔEAD为等腰直角三角形,
∴AE=DE, ∠EAD=∠EDA=45°,
∴∠CDE=135°
∵∠BAC=90°,
∴∠BAE=∠BAC+∠EAD=135°,
∴∠BAE=∠CDE,
在ΔABE和ΔDCE中
AB=DC
∵ ∠BAE=∠CDE
AE=DE
∴ΔABE≌ΔDCE
∴BE=EC,
∠AEB=∠DEC,
∵∠AED=90°,
∴∠BEC=90°,
∴BE⊥EC.4.已知:ΔABC中,AB=AC,AD是BC边上中线,AB的垂直平分线交AD于点O,∠B的平分线交AD于点I.
求证:(1)OA=OB=OC;
(2)点I到BC,CA,AB的距离相等.?ODCBAI┐┐┐┐EGF证明:(1)∵OG是AB的垂直平分线,
∴OA=OB,
又∵AB=AC,AD是BC边上的中线,
∴AD是BC边的垂直平分线,
∵点O在AD上,
∴OB=OC,
∴OA=OB=OC.(2)∵AB=AC,AD是BC边上的中线,
∴AD是∠BAC的平分线,又是BC边上的高,
∵OB平分∠ABC,IE⊥AB,IF⊥AC,
∴IE=IF=ID,
即:点I到BC,CA,AB的距离相等.5.已知:如图,AD是ΔABC的角平分线,DE⊥AB,
DF⊥AC,点E,F为垂足.求证:AD垂直平分EF.BCDFEA┐┐证明:∵AD是∠BAC的角平分线, DE⊥AB,DF⊥AC,
∴∠EAD=∠FAD,
∠AED=∠AFD=90°,
在ΔAED和ΔAFD中,
∠EAD=∠FAD,
∵ ∠AED=∠AFD,
AD=AD,
∴ΔAED≌ΔAFD,
∴AE=AF,DE=DF,
∴点A,D都在EF的垂直平分线上,
∴AD垂直平分EF.O6.已知:如图,ΔABC是等边三角形,BD是中线.点E在BC的延长线上,使CE=CD. 求证:DB=DE.ECBDA证明:∵ΔABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵BD是中线.
∴BD又是∠ABC的平分线,
∴∠DBC=30°,
∵CE=CD,
∴∠E=∠CDE,
又∵∠ACB=∠E+∠CDE=60°,
∴∠E=30°,
∴∠DBC=∠E,
∴DB=DE.7.求证:有两条高相等的三角形是等腰三角形.已知:如图,ΔABC中,BD,CE分别是AC,AB边上的高,且BD=CE. 求证:ΔABC是等腰三角形.DECBA┐┐证明:∵BD,CE分别是AC,AB边上的高,
∴∠ADB=∠AEC=90°,
在ΔABD和ΔACE中,
∠A=∠A,
∵ ∠ADB=∠AEC,
BD=CE,
∴ΔABD≌ΔACE,
∴AB=AC,
∴ΔABC是等腰三角形.8.已知:如图,ΔABC中,AD是BC边上的高,AB=AC,
∠BAC=120°,垂足分别是E,F.
求证:DE+DF= BC.┐┐FEBCDA证明:∵AB=AC,
∴∠B=∠C,
∵∠BAC=120°,
∴∠B=∠C=30°,
又∵DE⊥AB,DF⊥AC,
∴DE=?BD,DF=?DC,
∴DE+DF=?BD+?DC=?BC. 9.已知:如图,在ΔABC中,AB=AC,∠A=120°,AC的垂直平分线EF交AC于点E,交BC于点F.
求证:BF=2CF.┐FEBCA证明:连接AF,
∵AB=AC,
∴∠B=∠C,
∵∠A=120°,
∴∠B=∠C=30°,
∵EF是AC的垂直平分线,
∴AF=CF,
∴∠FAC=∠C=30°,
∴∠BAF=90°,
∴BF=2AF,
∴BF=2CF.10.已知:如图,AD⊥DE,BE⊥DE,AC,BC分别平分∠DAB,∠ABE,点C在线段DE上.求证:AB=AD+BE.DBECA┐┐F┐证明:过C作CF⊥AB,垂足为F,
又∵⊥AD,CE⊥BE,
AC平分∠DAB,BC平分∠ABE,
∴CD=CF=CE,
在RtΔACD和RtΔACF中,
AC=AC,
CD=CF,
∴RtΔACD≌RtΔACF,
∴AF=AD,
在RtΔBCE和RtΔBCF中,
BC=BC,
CE=CF,
∴RtΔBCE≌RtΔBCF,
∴BF=BE,
∴AB=AF+BF=AD+BE.11.已知:如图,在ΔABC中,∠A=90°,AB=AC,点D在BC上,BD=AB,作DE⊥BC,点E在边AC上.
求证:(1)BE平分∠ABC;(2)AE=ED=DC.CDEAB┐┐证明:(1)在RtΔABE和RtΔDBE中,
BE=BE,
AB=DB,
∴RtΔABE≌RtΔDBE,
∴∠ABE=∠DBE,
∴BE平分∠ABC;
(2)∵∠A=90°,AB=AC,
∴∠C=45°,
又∵DE⊥BC,
∴∠DEC=∠C=45°,
∴ED=DC,
∵RtΔABE≌RtΔDBE,∴AE=ED,
∴AE=ED=DC.12.已知:如图,在ΔABC中,以它的边AB,AC为边,分别在形外作等边三角形ABD,ACE,连接BE,DC.
求证:BE=DC.EDCBA证明:∵ΔABD和ΔACE都是等边三角形,
∴AB=AD,AE=AC,
∠BAD=∠CAE=60°,
∴∠BAE=∠DAC,
在ΔABE和ΔADC中,
AB=AD,
∵ ∠BAE=∠DAC,
AE=AC,
∴ΔABE≌ΔADC,
∴BE=DC.13.已知:如图,线段CD与∠AOB,通过作图求一点P,使PC=PD,并且点P到∠AOB两边的距离相等.OBDCA?14.已知:如图,RtΔABC中,∠C=90°,沿过点B的一条直线BE折叠这个三角形,使点C与边AB上的点D重合.要使D恰好为AB的中点,问还需增加一个什么条件?说明你增加的条件及依据.ABDEC可以增加:∠A=30°或BC=?AB,
或∠ABC=60°,或∠ABC=2∠A.理由:∵∠C=90°,∠A=30°,
∴BC=?AB,
由折叠可知BC=BD=?AB,
∴D为AB的中点.1.根据下列点的坐标的变化,判断它们进行了怎样的变换?
(1) (-3,-1) ( 3,-1);
(2) (-5, 6) (-5, 1);
(3) ( 4, 3) ( 4,-3);
(4) ( 2, -3) ( 3,-2).B组复习题答;:(1)关于y轴对称(或沿x轴方向向右平移6个单位).
(2)沿y轴方向向下平移5个单位(或关于直线y=3.5x对称).
(3)关于x轴对称(或沿y轴方向向下平移6个单位).
(4)关于直线y=-x对称(或先沿x轴方向向右平移1个单位,再沿y轴方向向上平移1个单位).2. BD是ΔABC的角平分线,BD的垂直平分线交CA的延长线于点E.求证:∠EAB=∠EBC.EDCBA┐证明:∵E在BD的垂直平分线上,
∴EB=ED,
∴∠EBD=∠EDB,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
又∵∠EAB=∠EDB+∠ABD,
∠EBC=∠EBD+∠DBC,
∴∠EAB=∠EBC3.已知:O是线段AB的中点,直线MN经过点O,点C,D在直线MN上,∠1=∠2=45°.
(1)若点C与点O重合[图(1)],请直接写出AC与BD的数量关系和位置关系;
(2)若点C,D不重合[图(2)],求证:AC=BD,AC⊥BD.CONANMDO(C)BAMDB211⌒⌒2⌒⌒(1)AC=BD,
AC⊥BD.3.已知:O是线段AB的中点,直线MN经过点O,点C,D在直线MN上,∠1=∠2=45°.
(2)若点C,D不重合[图(2)],求证:AC=BD,AC⊥BD.CONAMDB21⌒⌒E证明:过B作BE//AC,交MN于点E,
∴∠A=∠OBE,
又∵O是线段AB的中点,
∴OA=OB,
在ΔOAC和ΔOBE中,
∠A=∠OBE,
∵ ∠AOC=∠BOE,
OA=OB,
∴ΔOAC≌ΔOBE,
∴AC=BE,∠OCA=∠OEB,
∴∠1=∠BED
∴∠BED=∠2∵∠1=∠2=45°,
∴∠2=∠BED=45°,
∴BE=BD,∠DBE=90°,
∴AC=BD,BE⊥BD
∵BE//AC,
∴AC⊥BD4.已知:如图,在ΔABC中,∠ACB=90°,D,E是边AB上的两点,且AD=AC,BE=BC. 求证:∠DCE=45°.ACEDB证明:∵AD=AC,BE=BC,
∴∠ACD=∠ADC,∠BEC=∠BCE,
又∵∠A+∠ACD+∠ADC=180°,
∠B+∠BEC+∠BCE=180°,
∴∠A+2∠ACD=180°,∠B+2∠BCE=180°,
∴∠A+∠B+2∠ACD+2∠BCE=360°,
∴∠A+∠B+2∠ACD+2∠BCD+2∠DCE=360°,
∴∠A+∠B+2∠ACB+2∠DCE=360°,
又∵∠ACB=90°,∠A+∠B+∠ACB=180°,
∴2∠DCE=90°,
∴∠DCE=45°.5.已知:如图,点D在等边三角形ABC的边AC上,点E在边AB的延长线上,使BE=CD,DE交BC于点P.
求证:PD=PE.ABEPDCF证明:过D作DF//AB交BC于F,
∴∠CDF=∠A,∠CFD=∠CBA,
∠FDP=∠E,
又∵ΔABC是等边三角形,
∴∠A=∠CBA=∠C=60°,
∴∠C=∠CDF=∠CFD,
∴ΔCDF是等边三角形,
∴CD=FD,
∵BE=CD,
∴FD=BE,在ΔFDP和ΔBEP中,
∠FDP=∠E,
∵ ∠DPF=∠EPB,
FD=BE,
∴ΔFDP≌ΔBEP,
∴PD=PE.6.(1)已知:如图(1),在ΔABC中,∠ABC,∠ACB
的平分线交于点O,过点O的直线DE//BC,DE分别与AB,
AC交于点D,E.求证:BD+CE=DE.CBEODA(1)证明:∵DE//BC,
∴∠DOB=∠OBC,∠EOC=∠OCB,
又∵OB平分∠ABC,OC平分∠ACB,
∴∠OBD=∠OBC,∠OCE=∠OCB,
∴∠DOB=∠OBD,∠EOC=∠OCE,
∴BD=DO,CE=OE,
∴BD+CE=DO+OE,
∴BD+CE=DE.(2)将(1)题条件“∠ACB的平分线”改为“∠ACB
的外角平分线”,如图(2)所示.原来的关系式BD+CE
=DE还成立吗?如果不成立,你能推断出BD,CE,DE存
在的数量关系式吗?请证明你的推断.CBOEDA答:不成立.
BD-CE=DE.
证明:∵DE//BC,
∴∠DOB=∠OBC,∠EOC=∠OCF,
∵OB平分∠ABC,OC平分∠ACF,
∴∠OBD=∠OBC,∠OCE=∠OCF,
∴∠DOB=∠OBD,∠EOC=∠OCE,
∴BD=DO,CE=OE,
∴BD-CE=DO-OE,
∴BD-CE=DE.FC组复习题1.已知:等腰三角形ABC中,AB=AC.
(1)P为底边BC上任一点,自点P向两腰作垂线PE,PF,点E,F为垂足.求证:PE+PF等于定值;
(2)若点P在底边BC延长线上时,情况如何?FEPBAC┐┐证明:连接AP,设腰上的高为h1,
由SΔABC=SΔPAB+SΔPAC,得
?AB?PE+?AC?PF=?AB?h1.
又∵AB=AC,
∴ PE+PF=h1.
故,PE+PF等于定值.1.已知:等腰三角形ABC中,AB=AC.
(1)P为底边BC上任一点,自点P向两腰作垂线PE,PF,
点E,F为垂足.求证:PE+PF等于定值;
(2)若点P在底边BC延长线上时,情况如何?FEPCBA┐┐证明:连接AP,设腰上的高为h1,
由SΔABC=SΔPAB-SΔPAC,得
?AB?PE-?AC?PF=?AB?h1.
又∵AB=AC,
∴ PE-PF=h1.
故,PE-PF等于定值.如果,点P在底边CB延长线上时,有PF-PE=h1.2.已知:等边三角形ABC.
(1)P为ΔABC内任一点,自点P向三边作垂线PD,PE,
PF,点D,E,F为垂足.求证:PD+PE+PF等于定值;
(2)若点P在ΔABC外时,情况如何?PDFECBA┐┐┐证明:连接PA,PB,PC,
设等边ΔABC的高为h,
由SΔABC=SΔPAB+SΔPBC+SΔPAC,得
?AB?PD+?BC?PE+?AC?PF=?BC?h.
又∵AB=BC=AC,
∴PD+PE+PF=h,
故:PD+PE+PF等于定值.EDFPCBA┐┐┐当P在BA与CA的延长线所围成的区域内时,
证明:连接PA,PB,PC,
设等边ΔABC的高为h,
由SΔABC=SΔPBC-SΔPAB-SΔPAC,得
?BC?PE-?AB?PD-?AC?PF=?BC?h.
又∵AB=BC=AC,
∴PE-PD-PF=h,FEDPCBA┐┐┐当P在BA与BC的延长线所围成的区域内时,
证明:连接PA,PB,PC,
设等边ΔABC的高为h,
由SΔABC=SΔPBC+SΔPAB-SΔPAC,得
?BC?PE+?AB?PD-?AC?PF=?BC?h.
又∵AB=BC=AC,
∴PE+PD-PF=h,当P在AC与BC的延长线所围成的区域内时,
当P在AB与AC的延长线所围成的区域内时,
当P在AB与CB的延长线所围成的区域内时,
当P在CB与CA的延长线所围成的区域内时,
可以用类似的方法计算.
