4.3.2等比数列的前n项和公式课件(共44张PPT)
文档属性
| 名称 | 4.3.2等比数列的前n项和公式课件(共44张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-12 10:51:29 | ||
图片预览










文档简介
(共44张PPT)
4.3.2 等比数列的前 项和公式
高二 —人教版—数学选择性必修第二册—第四章
回顾旧知,引入新知
1.等比数列的定义:一般地,如果一个数列从第2项起,每一项与它的前一项的比
都等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,
公比通常用字母 表示(显然 ).
2.首项为 ,公比为 的等比数列 的通项公式为
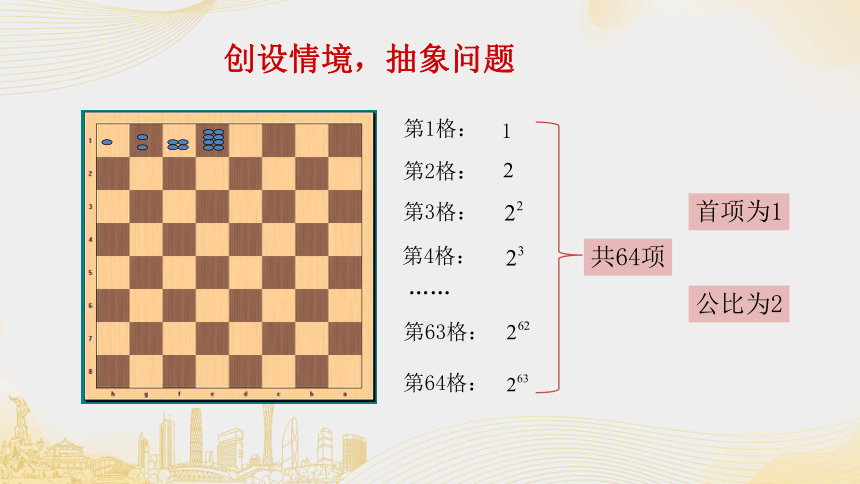
创设情境,抽象问题
国际象棋起源于古印度.相传国王要奖赏国际象棋的发明者,问他想要什么.发明者说:“请在棋盘的第1个格子里放上1颗麦粒,第2个格子里放上2颗麦粒,第3个格子里放上4颗麦粒……依次类推,每个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍,直到第64个格子.请给我足够的麦粒以实现上述要求.”国王觉得这个要求不高,就欣然同意了.
假定一千颗麦粒的质量约为40克,据查,2016-2017年度世界小麦产量约为7.5亿吨,根据以上数据,判断国王是否能实现他的诺言呢?
创设情境,抽象问题
第1格:
第2格:
第4格:
第3格:
第63格:
第64格:
1
……
首项为1
公比为2
共64项
这位聪明的发明者到底想要多少麦粒呢?
这实际上是首项为1,公比为2的等比数列的前64项的和,记为
创设情境,抽象问题
如何求一个等比数列的前 项和呢?
根据等比数列相邻两项的关系: ,上式可写成
探索新知,推导公式
假设等比数列
的首项为
,公比为 ,则
的前 项和是
化简,得
又因为
所以
化简,得
①
思考: 能两边同时除以
得到 吗?
①
即
探索新知,推导公式
因此,当 时,我们就得到等比数列的前 项和公式
又因为 ,所以公式还可以写成
思考1:当 时,等比数列的前 项和 等于多少?
当 时,我们发现等比数列 是以 为首项的常数列,
因此
①
思考2:还有其他方法吗?
探索新知,推导公式
回顾等差数列前 项求和公式推导过程,
等差数列前 项和的公式
关键利用等差
数列的公差
假设等差数列
的首项为
,公差为 ,
利用倒序相加法,
根据等差数列的性质: ,得到
得,
思考:如何利用等比数列的公比 推导等比数列 的前 项和公式?
在等比数列中,因
所以对于等比数列的前 项求和,不能照搬倒序相加的方法.
探索新知,推导公式
假设等比数列
的首项为
,公比为 ,则
的前 项和是
根据等比数列相邻两项的关系:
我们发现,如果用公比
乘②的两边,可得
根据等比数列的通项公式 ,上式可写成
②
③
在等比数列求和过程中,如何利用数列的公比 进行化简求和呢?
探索新知,推导公式
②③两式的右边有很多相同的项,由②-③可得
②
③
在等比数列求和过程中,如何利用数列的公比 进行化简求和呢?
即
探索新知,推导公式
当 时,我们就得到等比数列的前 项和公式
又因为 ,所以公式还可以写成
思考:除了以上两种推导方法外,还有其他推导方法吗?
当 时,等比数列 是以 为首项的常数列,
因此
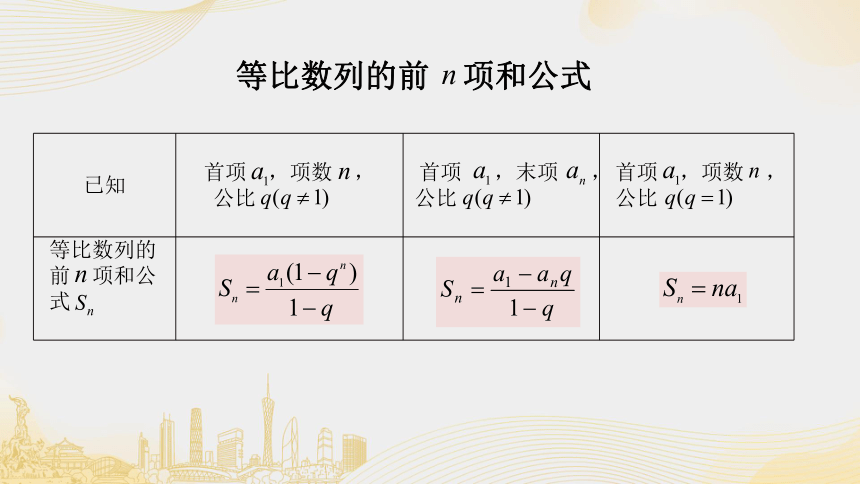
已知 首项 ,项数 , 公比 首项 ,末项 , 公比 首项 ,项数 ,
公比
等比数列的 前 项和公 式
等比数列的前 项和公式
回归情境,运用公式
有了上述公式,就可以解决本节开头提出的问题了.
可得
如果一千颗麦粒的质量约为40克,那么以上这些麦粒的总质量超过了7000亿吨,约是2016-2017年度世界小麦产量的981倍.因此,国王根本不可能实现他的诺言.
国际象棋起源于古印度.相传国王要奖赏国际象棋的发明者,问他想要什么.发明者说:“请在棋盘的第1个格子里放上1颗麦粒,第2个格子里放上2颗麦粒,第3个格子里放上4颗麦粒……依次类推,每个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍,直到第64个格子.请给我足够的麦粒以实现上述要求.”
由
例题讲解,学以致用
思考:如何利用等比数列前 项和公式求解?
例1. 已知 是等比数列.
(1)若 求 ;
解:因为
所以
例题讲解,学以致用
例1. 已知 是等比数列.
(2)若 求 ;
例题讲解,学以致用
例1. 已知 是等比数列.
(2)若 求 ;
所以
即
例题讲解,学以致用
解法:由 可得
又由 得
例1. 已知 是等比数列.
(2)若 求 ;
例题讲解,学以致用
例1. 已知 是等比数列.
(2)若 求 ;
解法1:由
又由 所以
所以
得
所以
例题讲解,学以致用
解法2:由
所以
得
又由 所以
所以
例1. 已知 是等比数列.
(3)若 求 .
例题讲解,学以致用
解:把 代入 得
整理,得
解得
例1. 已知 是等比数列.
(3)若 求 .
例题讲解,学以致用
例题讲解,学以致用
思考:
对于等比数列的相关量
,已知
几个量就可以确定其他量?
(1)
(2)
(3)
知三求二
例题讲解,学以致用
√
√
√
√
√
√
思考:对于等比数列的相关量 ,已知几个量就可以确定其他量?
(1)若 求 ;
(2)若 求 ;
(3)若 求 .
例题讲解,学以致用
例2. 已知等比数列 的公比 ,前 项和为 .
证明 成等比数列,并求这个数列的公比.
证明:利用等比数列 前 项和 的定义,得
例题讲解,学以致用
因为
证明:利用等比数列 前 项和的 定义,得
所以
例题讲解,学以致用
例2. 已知等比数列 的公比 ,前 项和为 .
证明 成等比数列,并求这个数列的公比.
想一想,直接使用等比数列前 项和的公式应如何证明该结论?
例题讲解,学以致用
例2. 已知等比数列 的公比 ,前 项和为 .
证明 成等比数列,并求这个数列的公比.
因为等比数列前 项和公式
分两种情况,所以在证明的时候,需要根据 的情况分类讨论.
证明:当 时,
所以 成等比数列,公比为1.
例题讲解,学以致用
例2. 已知等比数列 的公比 ,前 项和为 .
证明 成等比数列,并求这个数列的公比.
证明:当 时,
因为 为常数,所以 成等比数列,公比为 .
所以
讲解例题,提高能力
例3.如果一个等比数列前5项的和等于10,前10项的和等于50,那么这 个数列的公比是多少?
因为等比数列前 项和公式
分两种情况: 和 ,所以在证明的时候,也要根据 的情况分类讨论.
解法1:当 时,设等比数列的首项为 ,
由题意,得
所以,方程组无解.
讲解例题,提高能力
例3.如果一个等比数列前5项的和等于10,前10项的和等于50,那么这 个数列的公比是多少?
【解析】运用等比数列前 项和公式,列方程组进行运算
解法1:当 时,
①
②
由 得
所以
由题意,得
即
的首项为
,公比为 ,则
讲解例题,提高能力
例3.如果一个等比数列前5项的和等于10,前10项的和等于50,那么这 个数列的公比是多少?
【解析】运用等比数列前 项和的定义,进行化简运算
解法2:由题意,得
所以
所以
即
课堂小结,凝练升华
等比数列的前 项和公式
已知 首项 ,项数 , 公比 首项 ,末项 , 公比 首项 ,项数 ,
公比
等比数列的 前 项和公 式
等比数列的五个基本量 “知三求二”
4.3.2等比数列前 项和公式 答疑
高二 —人教版—数学选择性必修第二册—第四章
知 识 回 顾
等比数列的前 项和公式
已知量 首项 ,项数 , 公比 首项 ,末项 , 公比 首项 ,项数 ,
公比
等比数列的 前 项和公 式
等比数列的五个基本量 “知三求二”
讲 解 疑 难
我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有___盏灯.
例1.
(1)将文字语言转化为数学语言,建立数学模型.
(2)根据数学模型,运用公式求解.
解得
【解析】
所以,塔的顶层共有3盏灯.
3
去年某地产生的生活垃圾为20万吨,其中14万吨垃圾以填埋方式处理,6万吨垃圾以环保方式处理.预计每年生活垃圾的总量递增5%,同时,通过环保方式处理的垃圾量每年增加1.5万吨.为了确定处理生活垃圾的预算,请写出今年起 年内通过填埋方式处理的垃圾总量的计算公式,并计算从今年起5年内通过填埋方式处理的垃圾总量(精确到0.1万吨).
讲 解 疑 难
例2.
搜集整理信息
讲 解 疑 难
生活垃圾总量
年份 生活垃圾总量
今年(第一年)
第二年
第三年
... ...
第 年
由上表,可得
设从今年起每年生活垃圾的总量(单位:万吨)构成数列 ,则
根据等比数列的定义,数列 为等比数列,其中 , .
讲 解 疑 难
环保方式处理的垃圾量
年份 环保方式处理的垃圾量
今年(第一年)
第二年
第三年
... ...
第 年
由上表,可得
设从今年起每年以环保方式处理的垃圾量(单位:万吨)构成数列 ,则
根据等差数列的定义,数列 为等差数列,其中 , .
去年某地产生的生活垃圾为20万吨,其中14万吨垃圾以填埋方式处理,6万吨垃圾以环保方式处理.预计每年生活垃圾的总量递增5%,同时,通过环保方式处理的垃圾量每年增加1.5万吨.为了确定处理生活垃圾的预算,请写出今年起年内通过填埋方式处理的垃圾总量的计算公式,并计算从今年起5年内通过填埋方式处理的垃圾总量(精确到0.1万吨).
讲 解 疑 难
例2.
搜集整理信息
建立数学模型
设 年内通过填埋方式处理的垃圾总量为 (单位:万吨),则
分组求和
数列求和公式
讲 解 疑 难
去年某地产生的生活垃圾为20万吨,其中14万吨垃圾以填埋方式处理,6万吨垃圾以环保方式处理.预计每年生活垃圾的总量递增5%,同时,通过环保方式处理的垃圾量每年增加1.5万吨.为了确定处理生活垃圾的预算,请写出今年起年内通过填埋方式处理的垃圾总量的计算公式,并计算从今年起5年内通过填埋方式处理的垃圾总量(精确到0.1万吨).
讲 解 疑 难
例2.
搜集整理信息
建立数学模型
使用模型求解
所以,从今年起5年内,通过填埋方式处理的垃圾总量约为63.5万吨.
讲 解 疑 难
解:设从今年起每年生活垃圾的总量(单位:万吨)构成数列 ,每年以环保方式处理的垃圾量(单位:万吨)构成数列 , 年内通过填埋方式处理的垃圾总量为 (单位:万吨),则
因为
所以,从今年起5年内,通过填埋方式处理的垃圾总量约为63.5万吨.
讲 解 疑 难
搜集整理信息
建立数学模型
使用模型求解
解决数列应用题的一般步骤:
4.3.2 等比数列的前 项和公式
高二 —人教版—数学选择性必修第二册—第四章
回顾旧知,引入新知
1.等比数列的定义:一般地,如果一个数列从第2项起,每一项与它的前一项的比
都等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,
公比通常用字母 表示(显然 ).
2.首项为 ,公比为 的等比数列 的通项公式为
创设情境,抽象问题
国际象棋起源于古印度.相传国王要奖赏国际象棋的发明者,问他想要什么.发明者说:“请在棋盘的第1个格子里放上1颗麦粒,第2个格子里放上2颗麦粒,第3个格子里放上4颗麦粒……依次类推,每个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍,直到第64个格子.请给我足够的麦粒以实现上述要求.”国王觉得这个要求不高,就欣然同意了.
假定一千颗麦粒的质量约为40克,据查,2016-2017年度世界小麦产量约为7.5亿吨,根据以上数据,判断国王是否能实现他的诺言呢?
创设情境,抽象问题
第1格:
第2格:
第4格:
第3格:
第63格:
第64格:
1
……
首项为1
公比为2
共64项
这位聪明的发明者到底想要多少麦粒呢?
这实际上是首项为1,公比为2的等比数列的前64项的和,记为
创设情境,抽象问题
如何求一个等比数列的前 项和呢?
根据等比数列相邻两项的关系: ,上式可写成
探索新知,推导公式
假设等比数列
的首项为
,公比为 ,则
的前 项和是
化简,得
又因为
所以
化简,得
①
思考: 能两边同时除以
得到 吗?
①
即
探索新知,推导公式
因此,当 时,我们就得到等比数列的前 项和公式
又因为 ,所以公式还可以写成
思考1:当 时,等比数列的前 项和 等于多少?
当 时,我们发现等比数列 是以 为首项的常数列,
因此
①
思考2:还有其他方法吗?
探索新知,推导公式
回顾等差数列前 项求和公式推导过程,
等差数列前 项和的公式
关键利用等差
数列的公差
假设等差数列
的首项为
,公差为 ,
利用倒序相加法,
根据等差数列的性质: ,得到
得,
思考:如何利用等比数列的公比 推导等比数列 的前 项和公式?
在等比数列中,因
所以对于等比数列的前 项求和,不能照搬倒序相加的方法.
探索新知,推导公式
假设等比数列
的首项为
,公比为 ,则
的前 项和是
根据等比数列相邻两项的关系:
我们发现,如果用公比
乘②的两边,可得
根据等比数列的通项公式 ,上式可写成
②
③
在等比数列求和过程中,如何利用数列的公比 进行化简求和呢?
探索新知,推导公式
②③两式的右边有很多相同的项,由②-③可得
②
③
在等比数列求和过程中,如何利用数列的公比 进行化简求和呢?
即
探索新知,推导公式
当 时,我们就得到等比数列的前 项和公式
又因为 ,所以公式还可以写成
思考:除了以上两种推导方法外,还有其他推导方法吗?
当 时,等比数列 是以 为首项的常数列,
因此
已知 首项 ,项数 , 公比 首项 ,末项 , 公比 首项 ,项数 ,
公比
等比数列的 前 项和公 式
等比数列的前 项和公式
回归情境,运用公式
有了上述公式,就可以解决本节开头提出的问题了.
可得
如果一千颗麦粒的质量约为40克,那么以上这些麦粒的总质量超过了7000亿吨,约是2016-2017年度世界小麦产量的981倍.因此,国王根本不可能实现他的诺言.
国际象棋起源于古印度.相传国王要奖赏国际象棋的发明者,问他想要什么.发明者说:“请在棋盘的第1个格子里放上1颗麦粒,第2个格子里放上2颗麦粒,第3个格子里放上4颗麦粒……依次类推,每个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍,直到第64个格子.请给我足够的麦粒以实现上述要求.”
由
例题讲解,学以致用
思考:如何利用等比数列前 项和公式求解?
例1. 已知 是等比数列.
(1)若 求 ;
解:因为
所以
例题讲解,学以致用
例1. 已知 是等比数列.
(2)若 求 ;
例题讲解,学以致用
例1. 已知 是等比数列.
(2)若 求 ;
所以
即
例题讲解,学以致用
解法:由 可得
又由 得
例1. 已知 是等比数列.
(2)若 求 ;
例题讲解,学以致用
例1. 已知 是等比数列.
(2)若 求 ;
解法1:由
又由 所以
所以
得
所以
例题讲解,学以致用
解法2:由
所以
得
又由 所以
所以
例1. 已知 是等比数列.
(3)若 求 .
例题讲解,学以致用
解:把 代入 得
整理,得
解得
例1. 已知 是等比数列.
(3)若 求 .
例题讲解,学以致用
例题讲解,学以致用
思考:
对于等比数列的相关量
,已知
几个量就可以确定其他量?
(1)
(2)
(3)
知三求二
例题讲解,学以致用
√
√
√
√
√
√
思考:对于等比数列的相关量 ,已知几个量就可以确定其他量?
(1)若 求 ;
(2)若 求 ;
(3)若 求 .
例题讲解,学以致用
例2. 已知等比数列 的公比 ,前 项和为 .
证明 成等比数列,并求这个数列的公比.
证明:利用等比数列 前 项和 的定义,得
例题讲解,学以致用
因为
证明:利用等比数列 前 项和的 定义,得
所以
例题讲解,学以致用
例2. 已知等比数列 的公比 ,前 项和为 .
证明 成等比数列,并求这个数列的公比.
想一想,直接使用等比数列前 项和的公式应如何证明该结论?
例题讲解,学以致用
例2. 已知等比数列 的公比 ,前 项和为 .
证明 成等比数列,并求这个数列的公比.
因为等比数列前 项和公式
分两种情况,所以在证明的时候,需要根据 的情况分类讨论.
证明:当 时,
所以 成等比数列,公比为1.
例题讲解,学以致用
例2. 已知等比数列 的公比 ,前 项和为 .
证明 成等比数列,并求这个数列的公比.
证明:当 时,
因为 为常数,所以 成等比数列,公比为 .
所以
讲解例题,提高能力
例3.如果一个等比数列前5项的和等于10,前10项的和等于50,那么这 个数列的公比是多少?
因为等比数列前 项和公式
分两种情况: 和 ,所以在证明的时候,也要根据 的情况分类讨论.
解法1:当 时,设等比数列的首项为 ,
由题意,得
所以,方程组无解.
讲解例题,提高能力
例3.如果一个等比数列前5项的和等于10,前10项的和等于50,那么这 个数列的公比是多少?
【解析】运用等比数列前 项和公式,列方程组进行运算
解法1:当 时,
①
②
由 得
所以
由题意,得
即
的首项为
,公比为 ,则
讲解例题,提高能力
例3.如果一个等比数列前5项的和等于10,前10项的和等于50,那么这 个数列的公比是多少?
【解析】运用等比数列前 项和的定义,进行化简运算
解法2:由题意,得
所以
所以
即
课堂小结,凝练升华
等比数列的前 项和公式
已知 首项 ,项数 , 公比 首项 ,末项 , 公比 首项 ,项数 ,
公比
等比数列的 前 项和公 式
等比数列的五个基本量 “知三求二”
4.3.2等比数列前 项和公式 答疑
高二 —人教版—数学选择性必修第二册—第四章
知 识 回 顾
等比数列的前 项和公式
已知量 首项 ,项数 , 公比 首项 ,末项 , 公比 首项 ,项数 ,
公比
等比数列的 前 项和公 式
等比数列的五个基本量 “知三求二”
讲 解 疑 难
我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有___盏灯.
例1.
(1)将文字语言转化为数学语言,建立数学模型.
(2)根据数学模型,运用公式求解.
解得
【解析】
所以,塔的顶层共有3盏灯.
3
去年某地产生的生活垃圾为20万吨,其中14万吨垃圾以填埋方式处理,6万吨垃圾以环保方式处理.预计每年生活垃圾的总量递增5%,同时,通过环保方式处理的垃圾量每年增加1.5万吨.为了确定处理生活垃圾的预算,请写出今年起 年内通过填埋方式处理的垃圾总量的计算公式,并计算从今年起5年内通过填埋方式处理的垃圾总量(精确到0.1万吨).
讲 解 疑 难
例2.
搜集整理信息
讲 解 疑 难
生活垃圾总量
年份 生活垃圾总量
今年(第一年)
第二年
第三年
... ...
第 年
由上表,可得
设从今年起每年生活垃圾的总量(单位:万吨)构成数列 ,则
根据等比数列的定义,数列 为等比数列,其中 , .
讲 解 疑 难
环保方式处理的垃圾量
年份 环保方式处理的垃圾量
今年(第一年)
第二年
第三年
... ...
第 年
由上表,可得
设从今年起每年以环保方式处理的垃圾量(单位:万吨)构成数列 ,则
根据等差数列的定义,数列 为等差数列,其中 , .
去年某地产生的生活垃圾为20万吨,其中14万吨垃圾以填埋方式处理,6万吨垃圾以环保方式处理.预计每年生活垃圾的总量递增5%,同时,通过环保方式处理的垃圾量每年增加1.5万吨.为了确定处理生活垃圾的预算,请写出今年起年内通过填埋方式处理的垃圾总量的计算公式,并计算从今年起5年内通过填埋方式处理的垃圾总量(精确到0.1万吨).
讲 解 疑 难
例2.
搜集整理信息
建立数学模型
设 年内通过填埋方式处理的垃圾总量为 (单位:万吨),则
分组求和
数列求和公式
讲 解 疑 难
去年某地产生的生活垃圾为20万吨,其中14万吨垃圾以填埋方式处理,6万吨垃圾以环保方式处理.预计每年生活垃圾的总量递增5%,同时,通过环保方式处理的垃圾量每年增加1.5万吨.为了确定处理生活垃圾的预算,请写出今年起年内通过填埋方式处理的垃圾总量的计算公式,并计算从今年起5年内通过填埋方式处理的垃圾总量(精确到0.1万吨).
讲 解 疑 难
例2.
搜集整理信息
建立数学模型
使用模型求解
所以,从今年起5年内,通过填埋方式处理的垃圾总量约为63.5万吨.
讲 解 疑 难
解:设从今年起每年生活垃圾的总量(单位:万吨)构成数列 ,每年以环保方式处理的垃圾量(单位:万吨)构成数列 , 年内通过填埋方式处理的垃圾总量为 (单位:万吨),则
因为
所以,从今年起5年内,通过填埋方式处理的垃圾总量约为63.5万吨.
讲 解 疑 难
搜集整理信息
建立数学模型
使用模型求解
解决数列应用题的一般步骤:
