4.2.2等差数列的前n项和公式 课件(共31张PPT)
文档属性
| 名称 | 4.2.2等差数列的前n项和公式 课件(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-12 10:52:22 | ||
图片预览










文档简介
(共31张PPT)
4.2.2 等差数列的前项和公式
高二 —人教版—数学选择性必修第二册—第四章
高斯(Gauss,1777-1855),德国数学家,近代数学的奠基者之一,他与阿基米德、牛顿齐名,在天文学、大地测量学、磁学、光学等领域都作出过杰出贡献,是数学史上一颗光芒四射的巨星,被誉为“数学王子”.
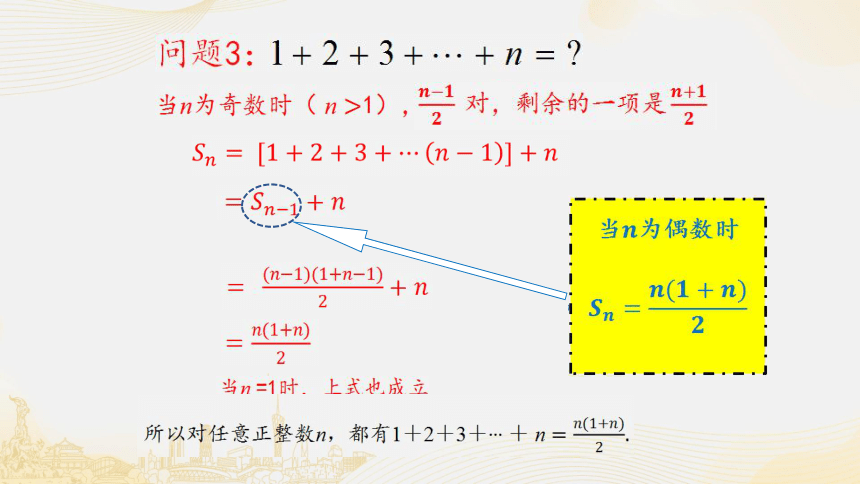
问题1:
高斯算法:
50对
思考:为什么会如此巧妙的有1+100=2+99=…=50+51,能从数列的角度给出解释吗?
设 an=n,则 a1=1,a2=2,a3=3,…
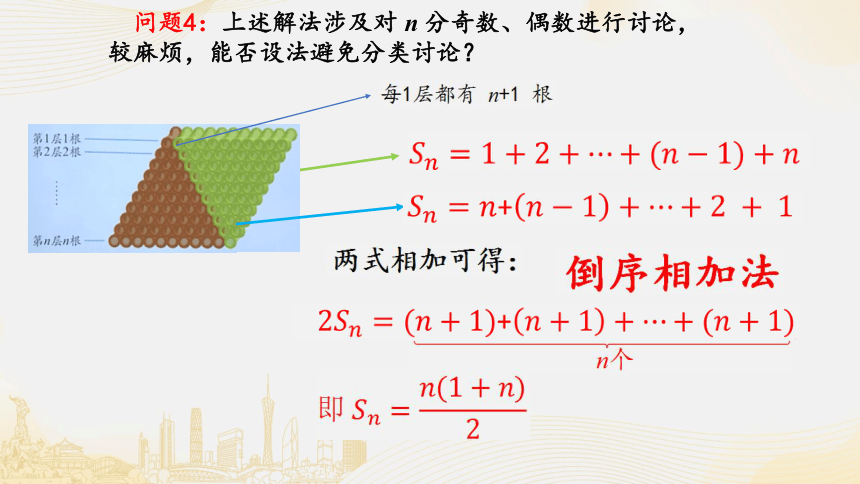
问题4:上述解法涉及对 n 分奇数、偶数进行讨论,较麻烦,能否设法避免分类讨论?
问题5. 这种方法能够推广到求等差数列的前项和吗?
等差数列的前n项和公式
项数
首项
末项
(1)
追问:你能用自己的语言来表述这个公式吗?
等差数列的前n项和公式
等差数列的前n项和公式
等差数列的前n项和公式
等差数列的前n项和公式
还有其他思路得到等差数列的前n项和公式(2)吗?
等差数列的前n项和公式
练习:等差数列{an}中,若, , 5,求n .
等差数列的前n项和公式
(1)式和(2)式共含有 n, a1 , an , d, Sn共五个量,已知其中三个,可以求得另外两个
例 已知一个等差数列前10项的和是310,前20项的和是1220. 由这些条件能确定这个等差数列的首项和公差吗
分析:
Sn
a1, d
a1, an
例 已知一个等差数列前10项的和是310,前20项的和是1220. 由这些条件能确定这个等差数列的首项和公差吗
a1, d
2个独立的方程
等差数列2个独立的条件
等差数列问题
基本量法
题后小结反思
课堂练习 某校新建一个报告厅,要求容纳800个座位,报告厅共有20排座位,从第2排起后一排都比前一排多2个座位. 问第1排应安排多少个座位?
课堂练习.某校新建一个报告厅,要求容纳800个座位,报告厅共有20排座位,从第2排起后一排都比前一排多两个座位. 问第1排应安排多少个座位?
等差数列的前n项和公式
课堂小结
基本量法
(转化与化归)
知三求二
(方程思想)
4.2.2 等差数列的前项和公式 答疑
高二 —人教版—数学选择性必修第二册—第四章
等差数列前n项和公式
知识梳理
基本量法
(转化与化归)
知三求二
(方程思想)
难点突破
例 已知等差数列{}的前n项和为Sn ,若=10,公差d=-2,则Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
.
例 已知等差数列{}的前n项和为Sn ,若=10,公差d=-2,则Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
难点突破
例 已知等差数列{}的前n项和为Sn ,若=10,公差d=-2,则Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
难点突破
,
.
例 已知等差数列{}的前n项和为Sn ,若=10,公差d=-2,则Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
难点突破
总结
等差数列的前n项和公式
等差数列前n项和最值问题
(3)
an=a1-(n-1)d
4.2.2 等差数列的前项和公式
高二 —人教版—数学选择性必修第二册—第四章
高斯(Gauss,1777-1855),德国数学家,近代数学的奠基者之一,他与阿基米德、牛顿齐名,在天文学、大地测量学、磁学、光学等领域都作出过杰出贡献,是数学史上一颗光芒四射的巨星,被誉为“数学王子”.
问题1:
高斯算法:
50对
思考:为什么会如此巧妙的有1+100=2+99=…=50+51,能从数列的角度给出解释吗?
设 an=n,则 a1=1,a2=2,a3=3,…
问题4:上述解法涉及对 n 分奇数、偶数进行讨论,较麻烦,能否设法避免分类讨论?
问题5. 这种方法能够推广到求等差数列的前项和吗?
等差数列的前n项和公式
项数
首项
末项
(1)
追问:你能用自己的语言来表述这个公式吗?
等差数列的前n项和公式
等差数列的前n项和公式
等差数列的前n项和公式
等差数列的前n项和公式
还有其他思路得到等差数列的前n项和公式(2)吗?
等差数列的前n项和公式
练习:等差数列{an}中,若, , 5,求n .
等差数列的前n项和公式
(1)式和(2)式共含有 n, a1 , an , d, Sn共五个量,已知其中三个,可以求得另外两个
例 已知一个等差数列前10项的和是310,前20项的和是1220. 由这些条件能确定这个等差数列的首项和公差吗
分析:
Sn
a1, d
a1, an
例 已知一个等差数列前10项的和是310,前20项的和是1220. 由这些条件能确定这个等差数列的首项和公差吗
a1, d
2个独立的方程
等差数列2个独立的条件
等差数列问题
基本量法
题后小结反思
课堂练习 某校新建一个报告厅,要求容纳800个座位,报告厅共有20排座位,从第2排起后一排都比前一排多2个座位. 问第1排应安排多少个座位?
课堂练习.某校新建一个报告厅,要求容纳800个座位,报告厅共有20排座位,从第2排起后一排都比前一排多两个座位. 问第1排应安排多少个座位?
等差数列的前n项和公式
课堂小结
基本量法
(转化与化归)
知三求二
(方程思想)
4.2.2 等差数列的前项和公式 答疑
高二 —人教版—数学选择性必修第二册—第四章
等差数列前n项和公式
知识梳理
基本量法
(转化与化归)
知三求二
(方程思想)
难点突破
例 已知等差数列{}的前n项和为Sn ,若=10,公差d=-2,则Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
.
例 已知等差数列{}的前n项和为Sn ,若=10,公差d=-2,则Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
难点突破
例 已知等差数列{}的前n项和为Sn ,若=10,公差d=-2,则Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
难点突破
,
.
例 已知等差数列{}的前n项和为Sn ,若=10,公差d=-2,则Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
难点突破
总结
等差数列的前n项和公式
等差数列前n项和最值问题
(3)
an=a1-(n-1)d
