27.1 图形的相似课时练习题(含答案)
文档属性
| 名称 | 27.1 图形的相似课时练习题(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 793.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-11 19:50:02 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
九年级数学下册《27.1图形的相似》课时练习题(含答案)
一、单选题
1.下列图形中,不是相似图形的一组是( )
A.B. C. D.
2.一个四边形各边长为2,3,4,5,另一个和它相似的四边形最长边为15,则的最短边长为( )
A.2 B.4 C.6 D.8
3.如图,点D、E分别在△ABC的边AB、BC上,下列条件中一定能判定DEAC的是( )
A. B. C. D.
4.如图,,若,,则( )
A. B. C. D.
5.如图,,,则的值是( )
A. B. C. D.
6.如图,四边形四边形,,,
,则∠D的度数为( )
A.100° B.110° C.120° D.130°
7.古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段分为两线段,,使得其中较长的一段是全长与较短的段的比例中项,即满足,后人把这个数称为“黄金分割”数,把点G称为线段的“黄金分割”点.如图,在中,已知,,若D,E是边的两个“黄金分割”点,则的面积为( )
A. B. C. D.
8.如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是( )
A.a=b B.a=2b C.a=2b D.a=4b
二、填空题
9.小颖在一本书上看到一个风筝模型,形状如图所示,其中对角线,并且两条对角线长分别为和.现在小颖照着模型按照1:3的比例放大制作一个大风筝,制作风筝需要彩色纸覆盖,而彩色纸是从一张刚好覆盖整个风筝的矩形彩色纸(如图中虚线所示)裁剪下来的,那么从四个角裁剪下来废弃不用的彩色纸的面积是_________.
10.下图是一架梯子的示意图,其中,且.为使其更稳固,在,间加绑一条安全绳(线段),量得,则________.
11.古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段分为两线段,使得其中较长的一段是全长与较短的段的比例中项,即满足,后人把这个数称为“黄金分割”数,把点G称为线段的“黄金分割”点.如图,在△ABC中,已知AB=AC=3,BC=4,若D,E是边的两个“黄金分割”点,则△ADE的面积为______.
12.如图,已知,三条对应边BC、CE、EF在同一条直线上,连接BG,分别交AC、DC、DE于点P、Q、K,其中,则图中三个阴影部分的面积和为__________.
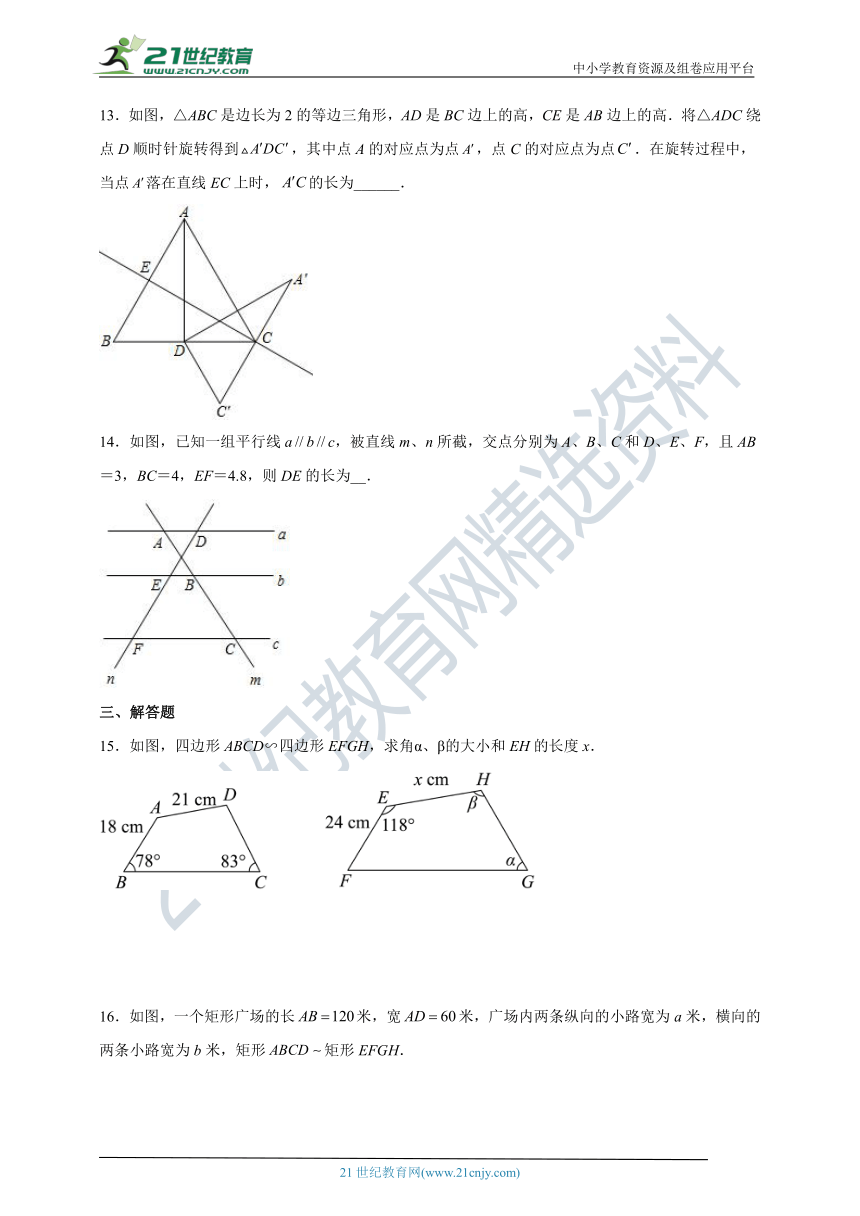
13.如图,△ABC是边长为2的等边三角形,AD是BC边上的高,CE是AB边上的高.将△ADC绕点D顺时针旋转得到,其中点A的对应点为点,点C的对应点为点.在旋转过程中,当点落在直线EC上时,的长为______.
14.如图,已知一组平行线abc,被直线m、n所截,交点分别为A、B、C和D、E、F,且AB=3,BC=4,EF=4.8,则DE的长为__.
三、解答题
15.如图,四边形ABCD∽四边形EFGH,求角α、β的大小和EH的长度x.
16.如图,一个矩形广场的长米,宽米,广场内两条纵向的小路宽为a米,横向的两条小路宽为b米,矩形矩形EFGH.
(1)求的值;
(2)若,求矩形EFGH的面积.
17.如图1,将A4纸2次折叠,发现第一次的折痕与A4纸较长的边重合,如图2,将1张A4纸对折,使其较长的边一分为二,沿折痕剪开,可得2张A5纸.
(1)A4纸较长边与较短边的比为 ;
(2)A4纸与A5纸是否为相似图形?请说明理由.
18.如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)在图(1)中,,分别是边,与网格线的交点.先将点绕点旋转得到点,画出点,再在上画点,使;
(2)在图(2)中,是边上一点,.先将绕点逆时针旋转,得到线段,画出线段,再画点,使,两点关于直线对称。
参考答案
1.D2.C3.B4.D5.B6.C7.A8.B
9.540
10.1.2
11.10-4
12.26
13.或
14.3.6
15.,,
16.(1)根据题意可知:HE=(60﹣2b)米,EF=(120﹣2a)米,
∵矩形ABCD∽矩形EFGH.
∴,
∴,
整理,得2b=a,
∴a:b=2:1;
(2)∵a=4,2b=a,
∴b=2,
∴矩形EFGH的面积
=EF HE
=(120﹣2a) (60﹣2b)
=(120﹣8)(60﹣4)
=112×56
=6272(米2).
答:矩形EFGH的面积为6272米2.
17.解:(1)如图1,设AB=x,
由上面两个图,由翻折的性质我们知道,∠ACF=∠HDF,∠ACB=∠HDB,∠ECF=45°,
∴∠BCF=∠BDF=90°,
又∵∠ACE=∠ACB+∠ECB=∠BCF=∠BCE+∠ECF,
∴∠ACB=∠ECF=45°,
∴BC=x,
∴BD=BC=x,AD=AB+BD=(+1)x,
∴EF=CE=AD=(+1)x,
∵DE=AC=AB=x,
∴DF=DE+EF=(+2)x,
∴,
故答案为:.
(2)由(1)知:A5纸长边为A4纸短边,长为(+1)x,A5纸短边长为()x,
∴对A5纸,长边:短边,
∴A4纸与A5纸相似.
18.(1)
解:作图如下:
取格点,连接,且,所以四边形是平行四边形,连接 ,与AC的交点就是点E,所以BE=EF,所以点F即为所求的点;
连接CF,交格线于点M,因为四边形ABCF是平行四边形,连接DM交AC于一点,该点就是所求的G点;
(2)
解:作图如下:
取格点D、E,连接DE,AC平行于DE,取格点R,连接BR并延长BR交DE于一点H,连接AH,此线段即为所求作线段;
理由如下:取格点W连接AW、CW,连接CR,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴ ,
∵点是的中点,
∴点是的中点,
即,
∴垂直平分,
∴.
连接,交AC于点,连接交于点,则该点就是点关于直线的对称点.
理由如下:∵垂直平分,
∴是等腰三角形,,
∴ ,
∴,
∴,
∴,两点关于直线对称.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学下册《27.1图形的相似》课时练习题(含答案)
一、单选题
1.下列图形中,不是相似图形的一组是( )
A.B. C. D.
2.一个四边形各边长为2,3,4,5,另一个和它相似的四边形最长边为15,则的最短边长为( )
A.2 B.4 C.6 D.8
3.如图,点D、E分别在△ABC的边AB、BC上,下列条件中一定能判定DEAC的是( )
A. B. C. D.
4.如图,,若,,则( )
A. B. C. D.
5.如图,,,则的值是( )
A. B. C. D.
6.如图,四边形四边形,,,
,则∠D的度数为( )
A.100° B.110° C.120° D.130°
7.古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段分为两线段,,使得其中较长的一段是全长与较短的段的比例中项,即满足,后人把这个数称为“黄金分割”数,把点G称为线段的“黄金分割”点.如图,在中,已知,,若D,E是边的两个“黄金分割”点,则的面积为( )
A. B. C. D.
8.如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是( )
A.a=b B.a=2b C.a=2b D.a=4b
二、填空题
9.小颖在一本书上看到一个风筝模型,形状如图所示,其中对角线,并且两条对角线长分别为和.现在小颖照着模型按照1:3的比例放大制作一个大风筝,制作风筝需要彩色纸覆盖,而彩色纸是从一张刚好覆盖整个风筝的矩形彩色纸(如图中虚线所示)裁剪下来的,那么从四个角裁剪下来废弃不用的彩色纸的面积是_________.
10.下图是一架梯子的示意图,其中,且.为使其更稳固,在,间加绑一条安全绳(线段),量得,则________.
11.古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段分为两线段,使得其中较长的一段是全长与较短的段的比例中项,即满足,后人把这个数称为“黄金分割”数,把点G称为线段的“黄金分割”点.如图,在△ABC中,已知AB=AC=3,BC=4,若D,E是边的两个“黄金分割”点,则△ADE的面积为______.
12.如图,已知,三条对应边BC、CE、EF在同一条直线上,连接BG,分别交AC、DC、DE于点P、Q、K,其中,则图中三个阴影部分的面积和为__________.
13.如图,△ABC是边长为2的等边三角形,AD是BC边上的高,CE是AB边上的高.将△ADC绕点D顺时针旋转得到,其中点A的对应点为点,点C的对应点为点.在旋转过程中,当点落在直线EC上时,的长为______.
14.如图,已知一组平行线abc,被直线m、n所截,交点分别为A、B、C和D、E、F,且AB=3,BC=4,EF=4.8,则DE的长为__.
三、解答题
15.如图,四边形ABCD∽四边形EFGH,求角α、β的大小和EH的长度x.
16.如图,一个矩形广场的长米,宽米,广场内两条纵向的小路宽为a米,横向的两条小路宽为b米,矩形矩形EFGH.
(1)求的值;
(2)若,求矩形EFGH的面积.
17.如图1,将A4纸2次折叠,发现第一次的折痕与A4纸较长的边重合,如图2,将1张A4纸对折,使其较长的边一分为二,沿折痕剪开,可得2张A5纸.
(1)A4纸较长边与较短边的比为 ;
(2)A4纸与A5纸是否为相似图形?请说明理由.
18.如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)在图(1)中,,分别是边,与网格线的交点.先将点绕点旋转得到点,画出点,再在上画点,使;
(2)在图(2)中,是边上一点,.先将绕点逆时针旋转,得到线段,画出线段,再画点,使,两点关于直线对称。
参考答案
1.D2.C3.B4.D5.B6.C7.A8.B
9.540
10.1.2
11.10-4
12.26
13.或
14.3.6
15.,,
16.(1)根据题意可知:HE=(60﹣2b)米,EF=(120﹣2a)米,
∵矩形ABCD∽矩形EFGH.
∴,
∴,
整理,得2b=a,
∴a:b=2:1;
(2)∵a=4,2b=a,
∴b=2,
∴矩形EFGH的面积
=EF HE
=(120﹣2a) (60﹣2b)
=(120﹣8)(60﹣4)
=112×56
=6272(米2).
答:矩形EFGH的面积为6272米2.
17.解:(1)如图1,设AB=x,
由上面两个图,由翻折的性质我们知道,∠ACF=∠HDF,∠ACB=∠HDB,∠ECF=45°,
∴∠BCF=∠BDF=90°,
又∵∠ACE=∠ACB+∠ECB=∠BCF=∠BCE+∠ECF,
∴∠ACB=∠ECF=45°,
∴BC=x,
∴BD=BC=x,AD=AB+BD=(+1)x,
∴EF=CE=AD=(+1)x,
∵DE=AC=AB=x,
∴DF=DE+EF=(+2)x,
∴,
故答案为:.
(2)由(1)知:A5纸长边为A4纸短边,长为(+1)x,A5纸短边长为()x,
∴对A5纸,长边:短边,
∴A4纸与A5纸相似.
18.(1)
解:作图如下:
取格点,连接,且,所以四边形是平行四边形,连接 ,与AC的交点就是点E,所以BE=EF,所以点F即为所求的点;
连接CF,交格线于点M,因为四边形ABCF是平行四边形,连接DM交AC于一点,该点就是所求的G点;
(2)
解:作图如下:
取格点D、E,连接DE,AC平行于DE,取格点R,连接BR并延长BR交DE于一点H,连接AH,此线段即为所求作线段;
理由如下:取格点W连接AW、CW,连接CR,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴ ,
∵点是的中点,
∴点是的中点,
即,
∴垂直平分,
∴.
连接,交AC于点,连接交于点,则该点就是点关于直线的对称点.
理由如下:∵垂直平分,
∴是等腰三角形,,
∴ ,
∴,
∴,
∴,两点关于直线对称.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
