5.3 圆周角（1）课件

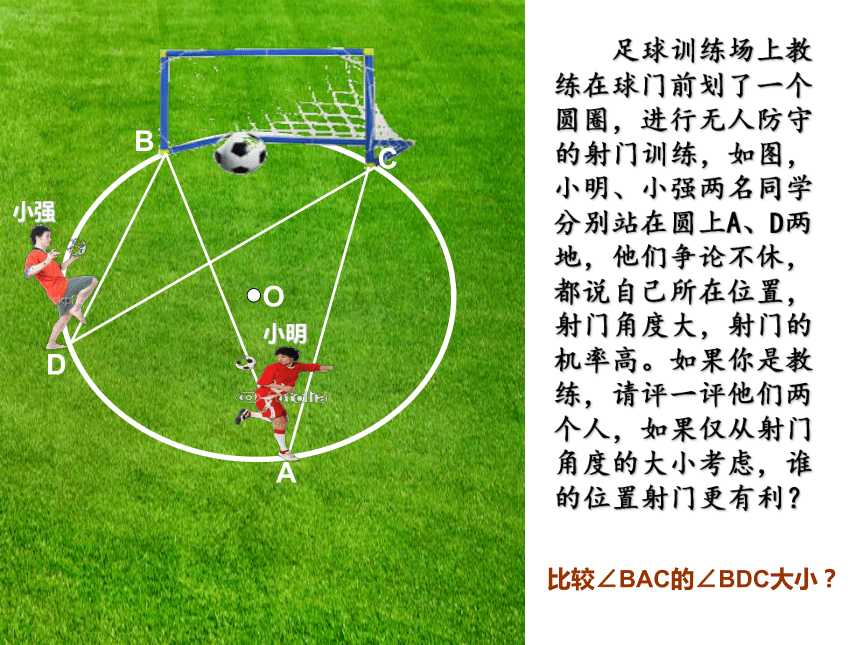
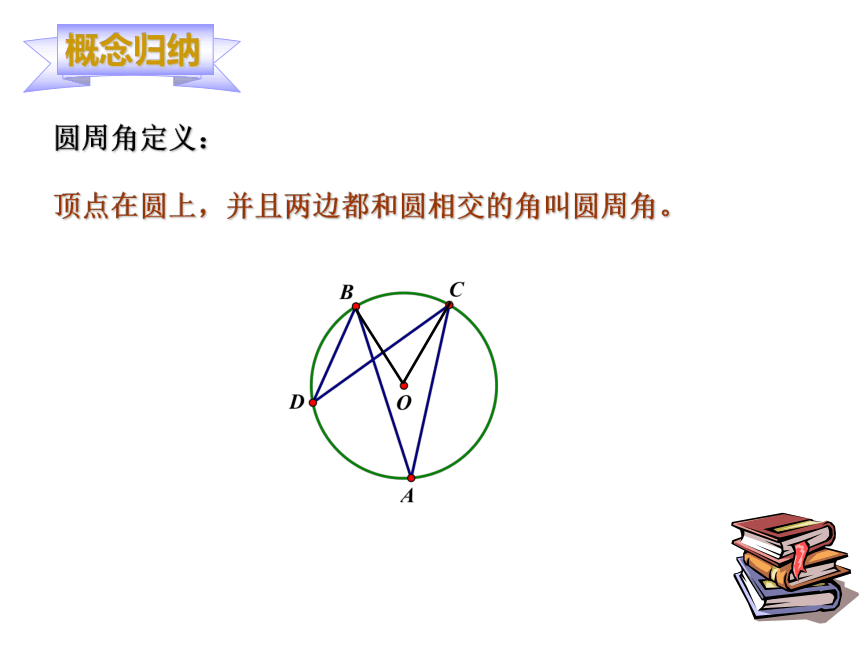
课件26张PPT。苏科版九年级数学（上册） 足球训练场上教练在球门前划了一个圆圈，进行无人防守的射门训练，如图，小明、小强两名同学分别站在圆上A、D两地，他们争论不休，都说自己所在位置，射门角度大，射门的机率高。如果你是教练，请评一评他们两个人，如果仅从射门角度的大小考虑，谁的位置射门更有利？ADBCO比较∠BAC的∠BDC大小？小明小强圆周角定义：
顶点在圆上，并且两边都和圆相交的角叫圆周角。辨一辨：
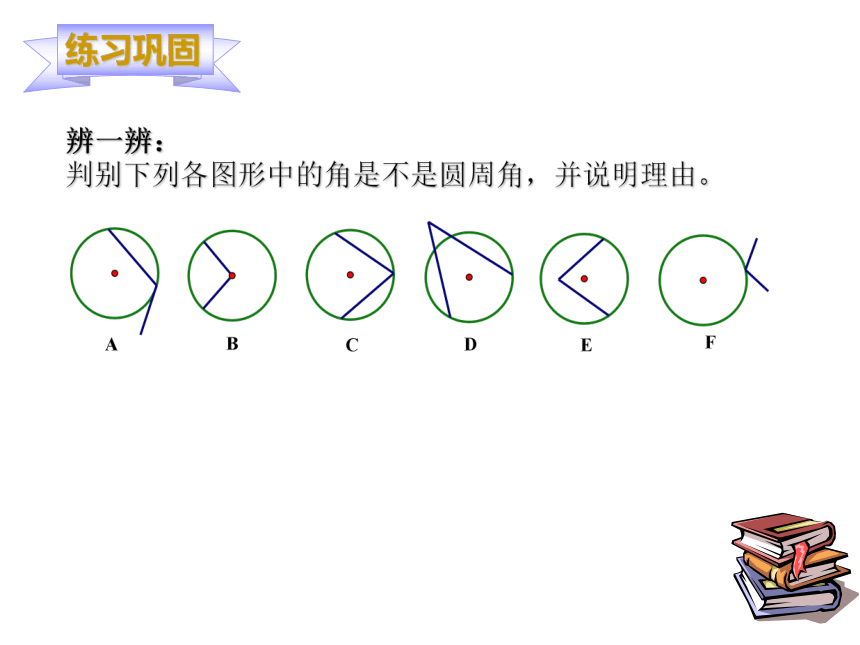
判别下列各图形中的角是不是圆周角，并说明理由。
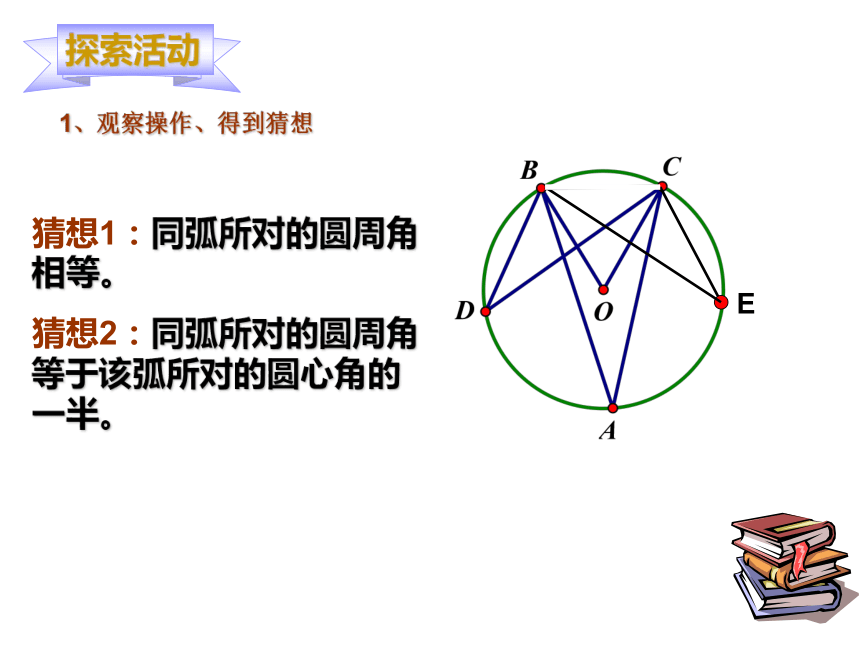
1、观察操作、得到猜想 E猜想1：同弧所对的圆周角相等。
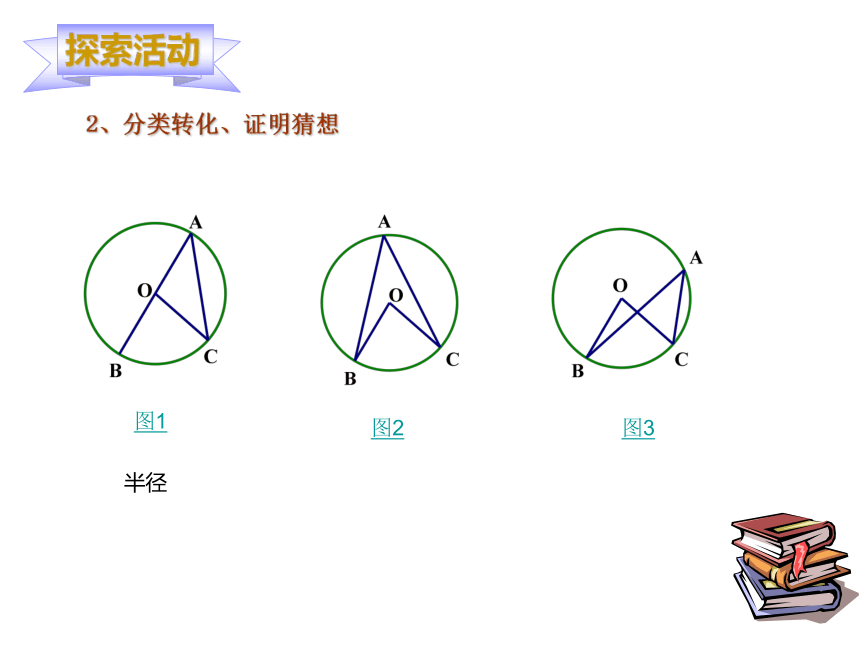
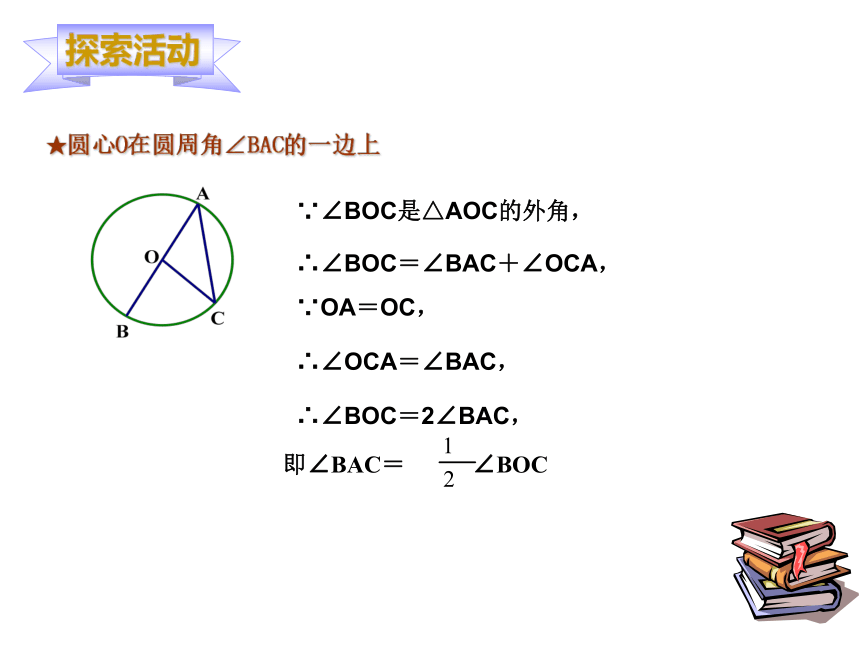
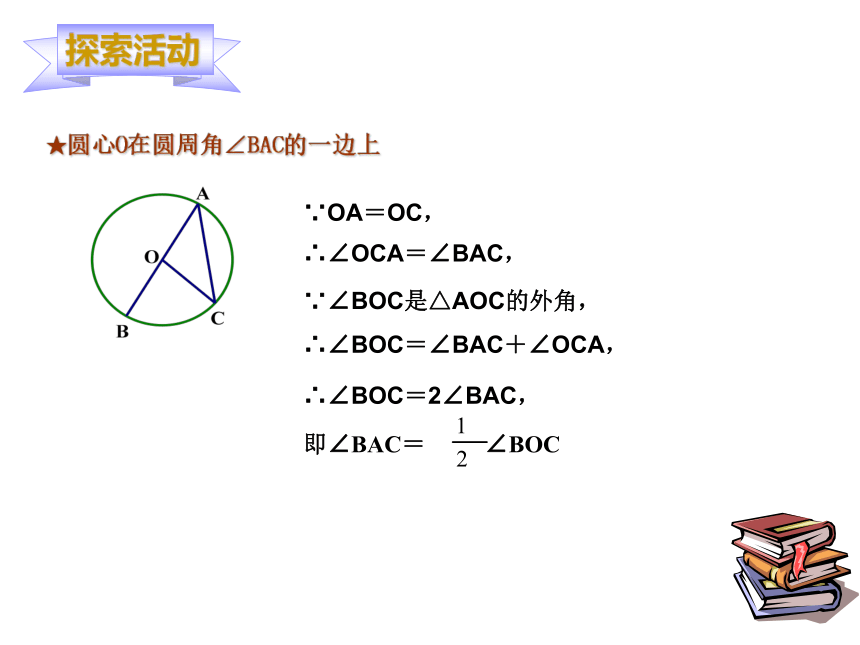
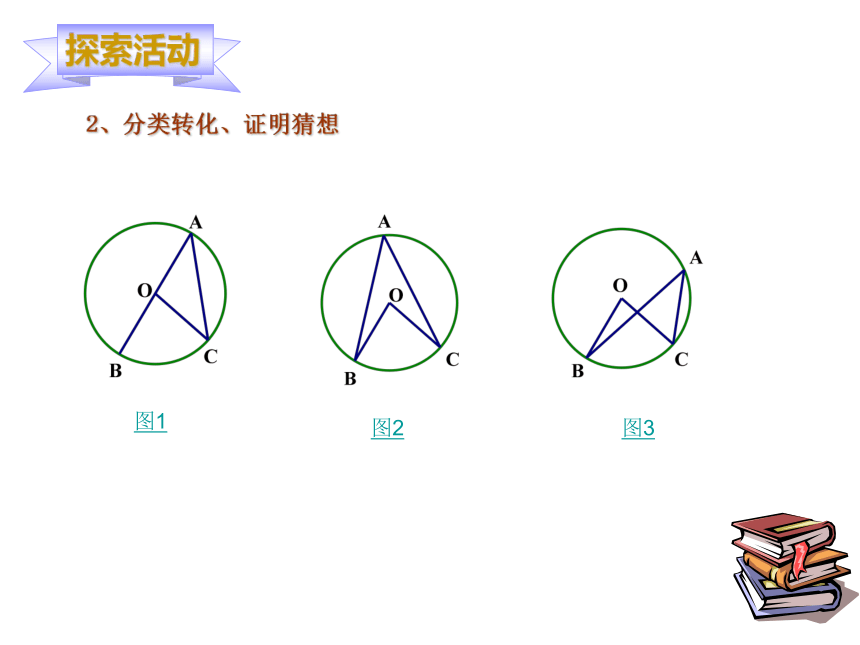
猜想2：同弧所对的圆周角等于该弧所对的圆心角的一半。2、分类转化、证明猜想图2图1图3半径★圆心O在圆周角∠BAC的一边上 ∵∠BOC是△AOC的外角，∴∠BOC＝∠BAC＋∠OCA，∵OA＝OC，∴∠OCA＝∠BAC， ∴∠BOC＝2∠BAC，★圆心O在圆周角∠BAC的一边上 ∵OA＝OC，∴∠OCA＝∠BAC， ∵∠BOC是△AOC的外角，∴∠BOC＝∠BAC＋∠OCA，∴∠BOC＝2∠BAC，2、分类转化、证明猜想图2图1图3★圆心O在圆周角∠BAC的内部D作直径AD， 于是2、分类转化、证明猜想图2图1图3★圆心O在圆周角∠BAC的外部D作直径AD， 于是结论：同弧所对的圆周角相等，都等于该弧所对的圆心角的一半。 在同圆或等圆中，把“同弧”改成“等弧”结论
是否依然成立？ 圆周角性质： 同弧或等弧所对的圆周角相等，都等于该弧所对的圆心角的一半。 1、如图1，点A、B、C、D在⊙O上，点A、D在点B、C所在直线的同侧，∠BAC＝35°,则
∠BDC ＝ °，理由是 ；
∠BOC ＝ °，理由是 。7035同弧所对的圆周角相等同弧所对的圆周角等于该弧所对的圆心角的一半。图12、图2中相等的圆周角有 。∠A=∠ D、∠B=∠ C图2ADBCO例1：站在点D的小强向后退了几步，退到了圆外，此时从射门角度大小考虑，小明A、小强D谁的位置射门更有利？例1：如图，点A、B、C在⊙O上，点D在圆外，CD、BD分别交⊙O于点E、F，比较∠BAC 与∠BDC的大小，并说明理由。小明例1：如图，点A、B、C在⊙O上，点D在圆外，CD、BD分别交⊙O于点E、F，比较∠BAC 与∠BDC的大小，并说明理由。
解：∠BAC＞∠BDC∵∠BFC是△CDF的一个外角∴∠BFC＞∠BDC∵∠BAC ＝∠BFC∴∠BAC＞∠BDC（同弧所对的圆周角相等）连接CFADBCO变式：站在点D的小强向前进了几步，进到了圆内，仅从射门角度大小考虑，此时小明A、 小强D谁的位置射门更有利？变式：如图，移动点D到圆内，其它条件不变，此时∠BAC与∠BDC
的大小又如何？并说明理由。
E1、数学知识
(1)圆周角的概念：(2)圆周角的性质：2、数学思想方法(1)分类思想(2)从特殊到一般思想(3)转化思想 1、必做题：教材第122页习题5.3的第1、3、4、5题；
2、选做题：
（1）已知：如图1，在⊙O中，弦AB的长度等于半径，则弦AB所对的
圆周角的大小为__ _____．
（2）如图2，∠BAC的两边均与⊙O相交，交点分别为B、D、C、E，试探究
∠BAC的大小与弧BC、弧DE的度数之间的关系．图1图2 近代伟大的科学家爱因斯坦在谈成功的秘诀时，写下了一个公式：A＝X＋Y＋Z。他解释道：A代表成功，X代表艰苦的劳动，Y代表正确的方法，Z代表少说空话。谢谢！