环状涂色问题
图片预览





文档简介
课件21张PPT。环状涂色问题中国行政地图
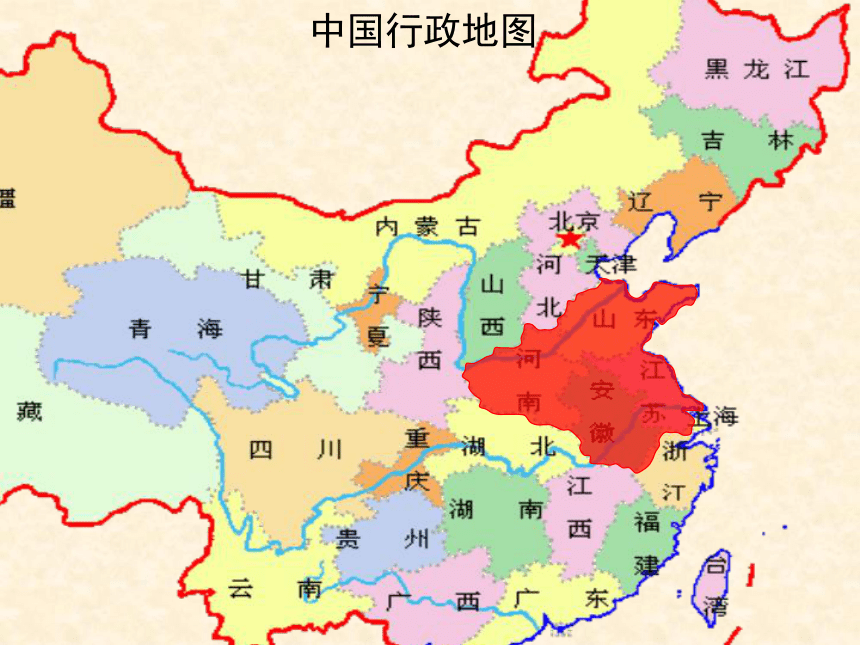
中国行政地图 给山东,河南,安徽,江苏四个地区涂色,相邻区域涂不同
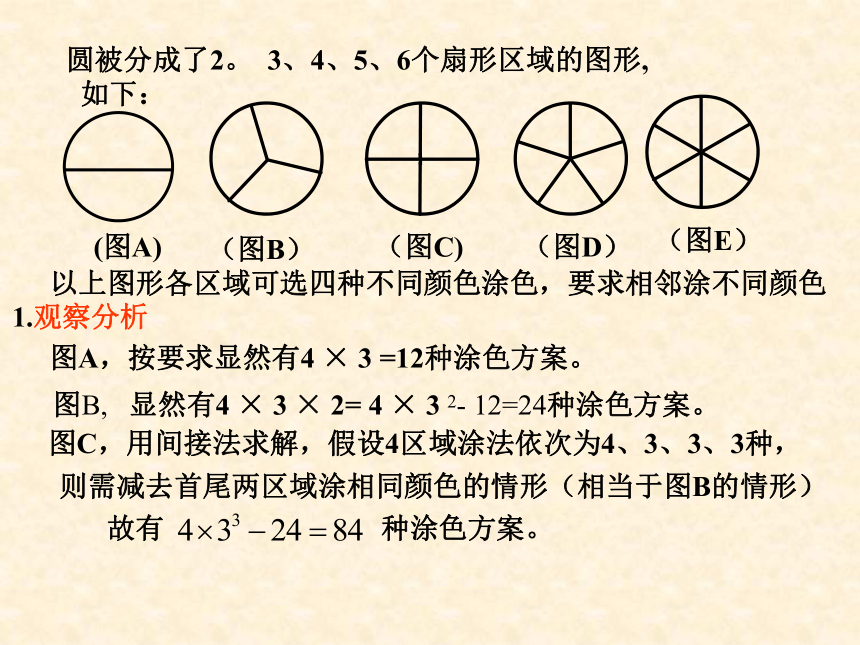
颜色,现有四种不同颜色可供使用,共有 —— 种不同涂法。问题84圆被分成了2。 3、4、5、6个扇形区域的图形,
如下:
?(图B)(图C)(图D) (图E) 图A,按要求显然有4 × 3 =12种涂色方案。图C,用间接法求解,假设4区域涂法依次为4、3、3、3种, 则需减去首尾两区域涂相同颜色的情形(相当于图B的情形) 故有 种涂色方案。 以上图形各区域可选四种不同颜色涂色,要求相邻涂不同颜色1.观察分析图B, 显然有4 × 3 × 2= 4 × 3 2- 12=24种涂色方案。 对图D,类似于图C的解法,假设5个区域涂法依次为4、3、
3、3、3种,则需减去首尾两区域涂相同颜色的情形(相当于
图C的情形)。 对图E,类似于图D的解法,假设6区域涂法依次为4、3、3、
3、3、3种,则需减去首尾两区域涂相同颜色的情形(相当于
图D的情形)。 如果n个区域有四种颜色可供选用,那么有多少种不同的涂法?2.猜想递推公式a2=4×3=(3+1)×3=a3=a4=a5=a6=3.猜想归纳通项an如果n个不同区域有m种颜色可供选用,那么有多少种不同的涂法?记为 4. 归纳相连构成n个区域, 、、、,现取种颜色对这n个区域涂色,每相邻的两个区域的涂色不同,
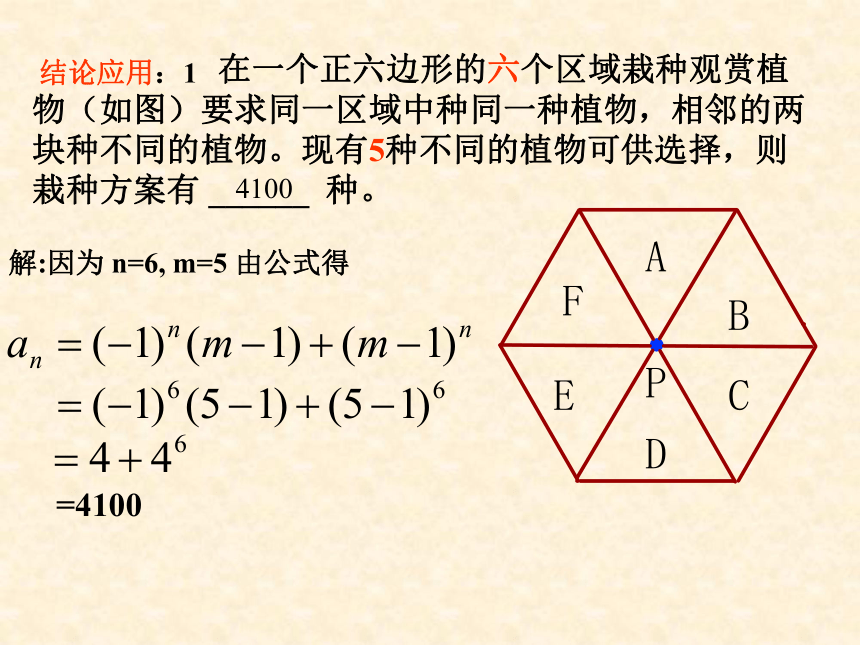
试求涂色的方案有多少种? 如图,已知p是环形内的一点,它与环形上的n(n ≥ 2)个顶点m(m≥3)故得递推公式为:(n≥2,m≥3)通项:P 在一个正六边形的六个区域栽种观赏植物(如图)要求同一区域中种同一种植物,相邻的两块种不同的植物。现有5种不同的植物可供选择,则栽种方案有 ______ 种。 4100结论应用:1解:因为 n=6, m=5 由公式得=4100应用2.(2008年全国)如图,一环形花坛分成A、B、C、D四块,现有 4种不同的花供选种,要在每块花坛里种一种花,且相邻的两块 种不同的花,则不同的种法总数为( )
A、96 B、84
C、60 D、48B如图,一个地区分为5个行政区域,现给地图着色,
要求相邻区域不得使用同一种颜色,现有四种颜色可供选择,则不同的着色方法有____种。 变式应用:1 (2003年高考题)所以涂色总数:M-不同颜色种数, n-除中心外的区域数中心为块的环状涂色问题涂法总数公式:2. (2003年全国高考——新课程卷·理工第15题)
某城市在中心广场建造一个花圃,花圃分为6个部分(如图),现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有_____种.(以数字作答)120引申练习:1(2005年潍坊模拟)将一个四棱锥的每一个
顶点染一种颜色,并使一条棱的两个端点异色,如果有5种不
同的颜色可选用,问有多少种不同的染色方法______种。用m种不同颜色涂n棱锥的顶点
涂法总数为:练习2:将5种颜色染n棱锥 的顶点,每个顶点染上一种颜色,
并使同一条棱的两端点异色。如果过有五种颜色可供
使用,那么不同的染色方法总数是__________________an=5[3n+(-1)n×3]
3. 将m(m≥4)种颜色染n(n≥3)棱锥的每个顶点染上一种颜
色,并使同一条棱的两端点异色。如果只有n种颜色可供使
用,那么不同的染色方法总数是an=_____________________m [(m-2)n+(-1)n(m-2) ]4. 将一个四棱锥的每一个面染一种颜色,并使相邻两面涂
异色,如果有5种不同的颜色可选用,问有______种不同的
染色方法。
420知识总结:1.中心为点的环状涂色问题涂法总数公式:(其中 n为不同区域数,m为不同颜色数)(n≥3,m≥4)3.用m不同颜色涂n棱锥的顶点涂法总数公式:2.中心为块的环状涂色问题涂法总数公式:m-不同颜色数, n-除中心外的区域数(n≥2,m≥3)(n≥3,m≥4)课后作业: (2003年全国高考题) 如图,一个地区分为5个行政区域,现给地图着色,
要求相邻区域不得使用同一种颜色,现有6种颜色可供选择,则不同的着色方法有____种。 1560 作业: (2003年全国高考——新课程卷·理工第15题)
某城市在中心广场建造一个花圃,花圃分为6个部分(如图),现
要栽种5种不同颜色的花,每部分栽种一种且相邻部分不能栽种
同样颜色的花,不同的栽种方法有____种.(以数字作答)3660再见
颜色,现有四种不同颜色可供使用,共有 —— 种不同涂法。问题84圆被分成了2。 3、4、5、6个扇形区域的图形,
如下:
?(图B)(图C)(图D) (图E) 图A,按要求显然有4 × 3 =12种涂色方案。图C,用间接法求解,假设4区域涂法依次为4、3、3、3种, 则需减去首尾两区域涂相同颜色的情形(相当于图B的情形) 故有 种涂色方案。 以上图形各区域可选四种不同颜色涂色,要求相邻涂不同颜色1.观察分析图B, 显然有4 × 3 × 2= 4 × 3 2- 12=24种涂色方案。 对图D,类似于图C的解法,假设5个区域涂法依次为4、3、
3、3、3种,则需减去首尾两区域涂相同颜色的情形(相当于
图C的情形)。 对图E,类似于图D的解法,假设6区域涂法依次为4、3、3、
3、3、3种,则需减去首尾两区域涂相同颜色的情形(相当于
图D的情形)。 如果n个区域有四种颜色可供选用,那么有多少种不同的涂法?2.猜想递推公式a2=4×3=(3+1)×3=a3=a4=a5=a6=3.猜想归纳通项an如果n个不同区域有m种颜色可供选用,那么有多少种不同的涂法?记为 4. 归纳相连构成n个区域, 、、、,现取种颜色对这n个区域涂色,每相邻的两个区域的涂色不同,
试求涂色的方案有多少种? 如图,已知p是环形内的一点,它与环形上的n(n ≥ 2)个顶点m(m≥3)故得递推公式为:(n≥2,m≥3)通项:P 在一个正六边形的六个区域栽种观赏植物(如图)要求同一区域中种同一种植物,相邻的两块种不同的植物。现有5种不同的植物可供选择,则栽种方案有 ______ 种。 4100结论应用:1解:因为 n=6, m=5 由公式得=4100应用2.(2008年全国)如图,一环形花坛分成A、B、C、D四块,现有 4种不同的花供选种,要在每块花坛里种一种花,且相邻的两块 种不同的花,则不同的种法总数为( )
A、96 B、84
C、60 D、48B如图,一个地区分为5个行政区域,现给地图着色,
要求相邻区域不得使用同一种颜色,现有四种颜色可供选择,则不同的着色方法有____种。 变式应用:1 (2003年高考题)所以涂色总数:M-不同颜色种数, n-除中心外的区域数中心为块的环状涂色问题涂法总数公式:2. (2003年全国高考——新课程卷·理工第15题)
某城市在中心广场建造一个花圃,花圃分为6个部分(如图),现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有_____种.(以数字作答)120引申练习:1(2005年潍坊模拟)将一个四棱锥的每一个
顶点染一种颜色,并使一条棱的两个端点异色,如果有5种不
同的颜色可选用,问有多少种不同的染色方法______种。用m种不同颜色涂n棱锥的顶点
涂法总数为:练习2:将5种颜色染n棱锥 的顶点,每个顶点染上一种颜色,
并使同一条棱的两端点异色。如果过有五种颜色可供
使用,那么不同的染色方法总数是__________________an=5[3n+(-1)n×3]
3. 将m(m≥4)种颜色染n(n≥3)棱锥的每个顶点染上一种颜
色,并使同一条棱的两端点异色。如果只有n种颜色可供使
用,那么不同的染色方法总数是an=_____________________m [(m-2)n+(-1)n(m-2) ]4. 将一个四棱锥的每一个面染一种颜色,并使相邻两面涂
异色,如果有5种不同的颜色可选用,问有______种不同的
染色方法。
420知识总结:1.中心为点的环状涂色问题涂法总数公式:(其中 n为不同区域数,m为不同颜色数)(n≥3,m≥4)3.用m不同颜色涂n棱锥的顶点涂法总数公式:2.中心为块的环状涂色问题涂法总数公式:m-不同颜色数, n-除中心外的区域数(n≥2,m≥3)(n≥3,m≥4)课后作业: (2003年全国高考题) 如图,一个地区分为5个行政区域,现给地图着色,
要求相邻区域不得使用同一种颜色,现有6种颜色可供选择,则不同的着色方法有____种。 1560 作业: (2003年全国高考——新课程卷·理工第15题)
某城市在中心广场建造一个花圃,花圃分为6个部分(如图),现
要栽种5种不同颜色的花,每部分栽种一种且相邻部分不能栽种
同样颜色的花,不同的栽种方法有____种.(以数字作答)3660再见
