2023届中考数学专项练习 圆的有关概念及其性质(A)(含解析)
文档属性
| 名称 | 2023届中考数学专项练习 圆的有关概念及其性质(A)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-09 21:47:39 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
圆的有关概念及其性质(A)
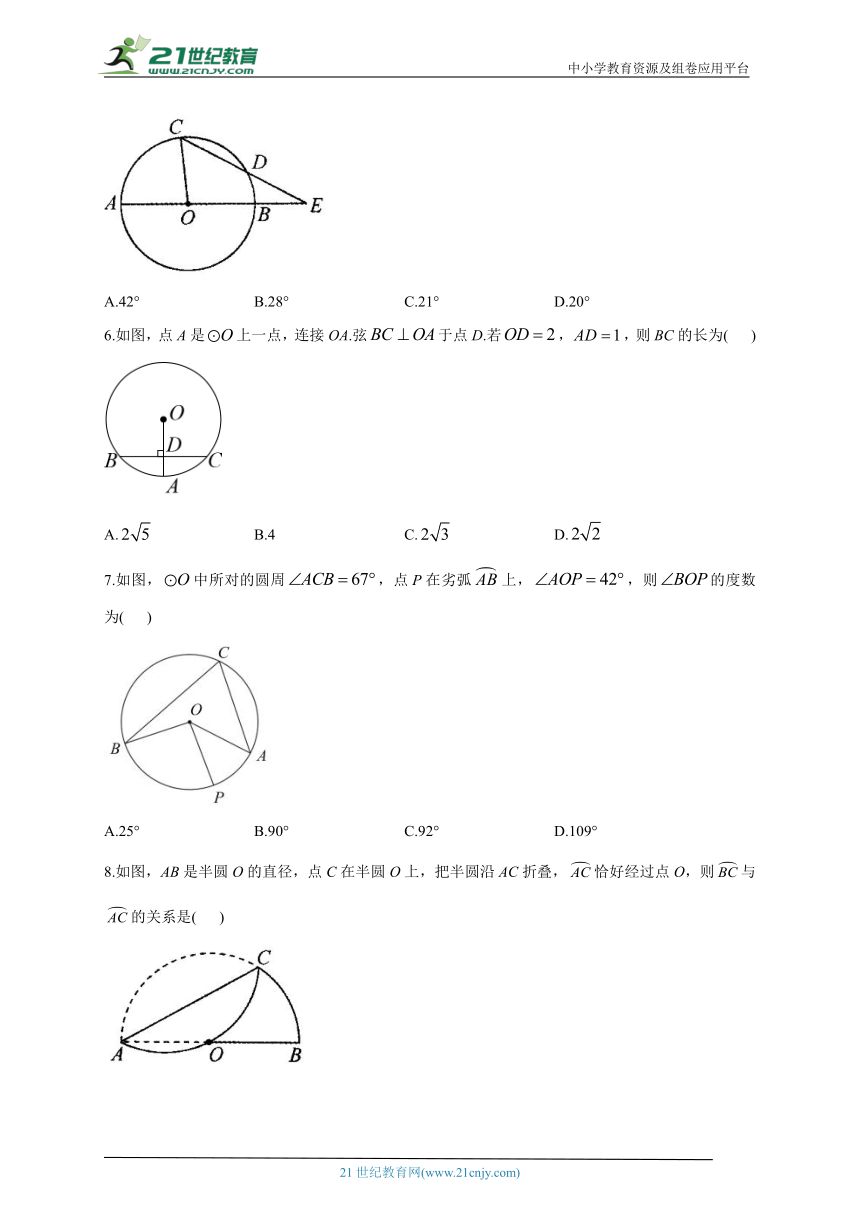
1.下列说法中,不正确的是( )
A.圆既是轴对称图形,又是中心对称图形
B.圆绕着它的圆心旋转任意角度,都能与自身重合
C.圆的对称轴有无数条,对称中心只有一个
D.圆的每一条直径都是它的对称轴
2.如图,AB是的直径,,,则的度数是( )
A.52° B.57° C.66° D.78°
3.如图,点A,B,C在上,,则等于( )
A.36° B.54° C.18° D.28°
4.如图,在中,,,则的度数是( )
A.64° B.58° C.32° D.26°
5.如图,的直径AB与弦CD的延长线交于点E,若,,则等于( )
A.42° B.28° C.21° D.20°
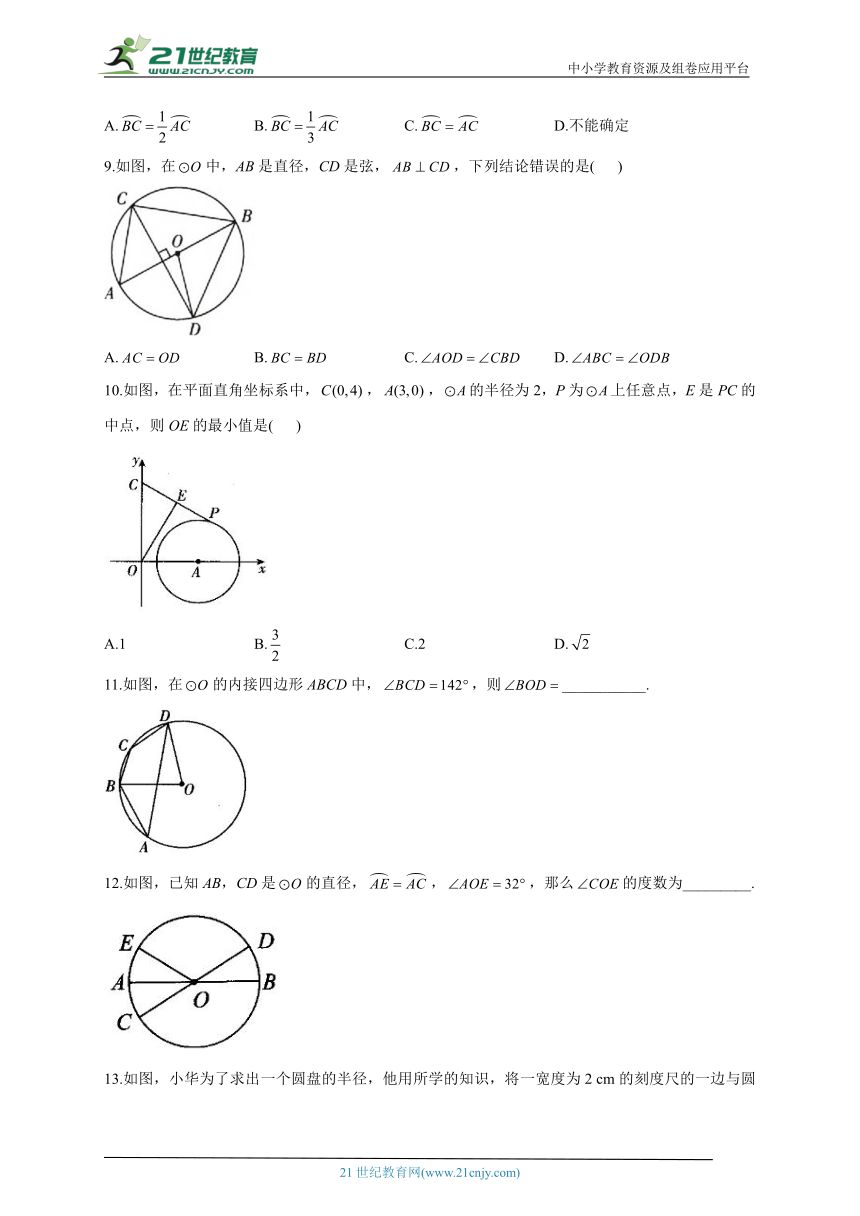
6.如图,点A是上一点,连接OA.弦于点D.若,,则BC的长为( )
A. B.4 C. D.
7.如图,中所对的圆周,点P在劣弧上,,则的度数为( )
A.25° B.90° C.92° D.109°
8.如图,AB是半圆O的直径,点C在半圆O上,把半圆沿AC折叠,恰好经过点O,则与的关系是( )21世纪教育网版权所有
A. B. C. D.不能确定
9.如图,在中,AB是直径,CD是弦,,下列结论错误的是( )
A. B. C. D.
10.如图,在平面直角坐标系中,,,的半径为2,P为上任意点,E是PC的中点,则OE的最小值是( )21教育网
A.1 B. C.2 D.
11.如图,在的内接四边形ABCD中,,则___________.
12.如图,已知AB,CD是的直径,,,那么的度数为_________.
13.如图,小华为了求出一个圆盘的半径,他用所学的知识,将一宽度为2 cm的刻度尺的一边与圆盘相切,另一边与圆盘边缘两个交点处的读数分别是“4”和“16”(单位:),请你帮小华算出圆盘的半径是_________cm.21cnjy.com
14.如图,AB是半圆O的直径,点D在半圆O上,,,C是弧BD上的一个动点,连接AC,过D点作于H.连接BH,则在点C移动的过程中,线段BH的最小值是______.
15.如图,四边形ABCD是的内接四边形,,,.
(1)求的度数;
(2)求的度数.
答案以及解析
1.答案:D
解析:圆既是轴对称图形,又是中心对称图形,所以A选项不符合题意;圆是一个特殊的中心对称图形,圆绕着它的圆心旋转任意角度都能与自身重合,所以B选项不符合题意;圆的对称轴是过圆心的直线,这样的直线有无数条,对称中心只有一个,是圆心,所以C选项不符合题意;直径是线段而不是直线,不能说直径是圆的对称轴,所以D选项符合题意.故选D.2·1·c·n·j·y
2.答案:B
解析:,,,.
3.答案:A
解析:根据圆周角定理可知,,则,故选A.
4.答案:D
解析:连接AO,如图.
由,得,.
.
,.在中,,.故选D.
5.答案:B
解析:连接OD,,,,,,,,,,,.故选B.
6.答案:A
解析:连接OB和OC,如图,
,
,
在中,
,
在中,
,
.
故选:A.
7.答案:C
解析:中所对的圆周,
点P在劣弧上,,
,
故选C.
8.答案:A
解析:如图,连接BC,过点O作于点D交半圆O于点E,
,
为的中位线,
,.
把半圆沿AC折叠,恰好经过点O,
,,连接EC,
则四边形OBCE是平行四边形,
又,
是菱形,,.故选A.
9.答案:A
解析:由已知条件无法推出弦AC与半径OD相等,故选项A错误.是的直径,CD是弦,且,是CD的垂直平分线,,,.又,,,,故选项B,C,D正确.故选A.
10.答案:B
解析:如图,连接AC,取AC的中点H,连接EH,OH, AP.点E,H分别是PC,AC的中点,,点E的运动轨迹是以H为圆心,半径为1的圆.,,,,OE的最小值为.故选B.21·cn·jy·com
11.答案:76°
解析:四边形ABCD是的内接四边形,.,,.
12.答案:64°
解析:,.又,,.
13.答案:10
解析:如图,设圆的圆心为O,刻度尺与圆盘的切点为点C,与圆盘边缘相交的两个交点分别为A,B,连接OB,OC交AB于点D.,.www.21-cn-jy.com
由图知,,,
.设圆的半径为r,则,.
在中,根据勾股定理,得,,
解得.圆盘的半径是10 cm.
14.答案:,
解析:连接BD,取AD的中点E,连接BE,
,
H点在以E为圆心,AE为半径的圆上,
当B、H、E三点共线时,BH最小,
AB是直径,
,
,,
,,
在中,,
,
故答案为:.
15.答案:(1)
(2)
解析:(1),
,
,
;
(2)由圆周角定理得:,
,
四边形ABCD是的内接四边形,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
圆的有关概念及其性质(A)
1.下列说法中,不正确的是( )
A.圆既是轴对称图形,又是中心对称图形
B.圆绕着它的圆心旋转任意角度,都能与自身重合
C.圆的对称轴有无数条,对称中心只有一个
D.圆的每一条直径都是它的对称轴
2.如图,AB是的直径,,,则的度数是( )
A.52° B.57° C.66° D.78°
3.如图,点A,B,C在上,,则等于( )
A.36° B.54° C.18° D.28°
4.如图,在中,,,则的度数是( )
A.64° B.58° C.32° D.26°
5.如图,的直径AB与弦CD的延长线交于点E,若,,则等于( )
A.42° B.28° C.21° D.20°
6.如图,点A是上一点,连接OA.弦于点D.若,,则BC的长为( )
A. B.4 C. D.
7.如图,中所对的圆周,点P在劣弧上,,则的度数为( )
A.25° B.90° C.92° D.109°
8.如图,AB是半圆O的直径,点C在半圆O上,把半圆沿AC折叠,恰好经过点O,则与的关系是( )21世纪教育网版权所有
A. B. C. D.不能确定
9.如图,在中,AB是直径,CD是弦,,下列结论错误的是( )
A. B. C. D.
10.如图,在平面直角坐标系中,,,的半径为2,P为上任意点,E是PC的中点,则OE的最小值是( )21教育网
A.1 B. C.2 D.
11.如图,在的内接四边形ABCD中,,则___________.
12.如图,已知AB,CD是的直径,,,那么的度数为_________.
13.如图,小华为了求出一个圆盘的半径,他用所学的知识,将一宽度为2 cm的刻度尺的一边与圆盘相切,另一边与圆盘边缘两个交点处的读数分别是“4”和“16”(单位:),请你帮小华算出圆盘的半径是_________cm.21cnjy.com
14.如图,AB是半圆O的直径,点D在半圆O上,,,C是弧BD上的一个动点,连接AC,过D点作于H.连接BH,则在点C移动的过程中,线段BH的最小值是______.
15.如图,四边形ABCD是的内接四边形,,,.
(1)求的度数;
(2)求的度数.
答案以及解析
1.答案:D
解析:圆既是轴对称图形,又是中心对称图形,所以A选项不符合题意;圆是一个特殊的中心对称图形,圆绕着它的圆心旋转任意角度都能与自身重合,所以B选项不符合题意;圆的对称轴是过圆心的直线,这样的直线有无数条,对称中心只有一个,是圆心,所以C选项不符合题意;直径是线段而不是直线,不能说直径是圆的对称轴,所以D选项符合题意.故选D.2·1·c·n·j·y
2.答案:B
解析:,,,.
3.答案:A
解析:根据圆周角定理可知,,则,故选A.
4.答案:D
解析:连接AO,如图.
由,得,.
.
,.在中,,.故选D.
5.答案:B
解析:连接OD,,,,,,,,,,,.故选B.
6.答案:A
解析:连接OB和OC,如图,
,
,
在中,
,
在中,
,
.
故选:A.
7.答案:C
解析:中所对的圆周,
点P在劣弧上,,
,
故选C.
8.答案:A
解析:如图,连接BC,过点O作于点D交半圆O于点E,
,
为的中位线,
,.
把半圆沿AC折叠,恰好经过点O,
,,连接EC,
则四边形OBCE是平行四边形,
又,
是菱形,,.故选A.
9.答案:A
解析:由已知条件无法推出弦AC与半径OD相等,故选项A错误.是的直径,CD是弦,且,是CD的垂直平分线,,,.又,,,,故选项B,C,D正确.故选A.
10.答案:B
解析:如图,连接AC,取AC的中点H,连接EH,OH, AP.点E,H分别是PC,AC的中点,,点E的运动轨迹是以H为圆心,半径为1的圆.,,,,OE的最小值为.故选B.21·cn·jy·com
11.答案:76°
解析:四边形ABCD是的内接四边形,.,,.
12.答案:64°
解析:,.又,,.
13.答案:10
解析:如图,设圆的圆心为O,刻度尺与圆盘的切点为点C,与圆盘边缘相交的两个交点分别为A,B,连接OB,OC交AB于点D.,.www.21-cn-jy.com
由图知,,,
.设圆的半径为r,则,.
在中,根据勾股定理,得,,
解得.圆盘的半径是10 cm.
14.答案:,
解析:连接BD,取AD的中点E,连接BE,
,
H点在以E为圆心,AE为半径的圆上,
当B、H、E三点共线时,BH最小,
AB是直径,
,
,,
,,
在中,,
,
故答案为:.
15.答案:(1)
(2)
解析:(1),
,
,
;
(2)由圆周角定理得:,
,
四边形ABCD是的内接四边形,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
