第24章解直角三角形课时练习及答案(共10课时)
文档属性
| 名称 | 第24章解直角三角形课时练习及答案(共10课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 733.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-01-05 00:00:00 | ||
图片预览



文档简介
第24章解直角三角形
24.1锐角的三角函数
第1课时 正切
知识点一 正切的意义
1.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,
①tanA= = ;
②tanB= = ;
③tan∠ACD= ;
④tan∠BCD= .
2.在Rt△中,,若三角形的各边都扩大3倍,则的数值( ).
A.没有变化 B.扩大了3倍 C.缩小到 D.不能确定
3.在Rt△中,,,,则边的长为( ).
A. B. C. D.
4.如图,正方形ABCD的边长为4,点M在边DC上,M、N 两点关于对角线AC对称,若DM=1,则tan∠ADN= .
5.如图,在中,,于,若,,请你求出的值.
知识点一 坡度与坡角
6.正切常用来描述坡面的坡度,如图,坡面的铅直高度和水平宽度的比叫做坡面的 (或 ),记作,即 .
7.已知一个斜坡的长为10米,高度为8米,则坡度为 .
8.小敏沿着直坡度i=1:的山坡向上走了50m,这时他离地面______m.
9.有一拦水坝的横断面是等腰梯形,它的上底长为6米,下底长为10米,高为米,那么此拦水坝斜坡的坡度为 .
技能点一 求实际问题中的正切值
10.为测量如图所示上山坡道的倾斜度,小明测得图中所示的数据(单位:米),则该坡道倾斜角α的正切值是
A. B.4 C. D.
技能点二 坡度在生活中的应角
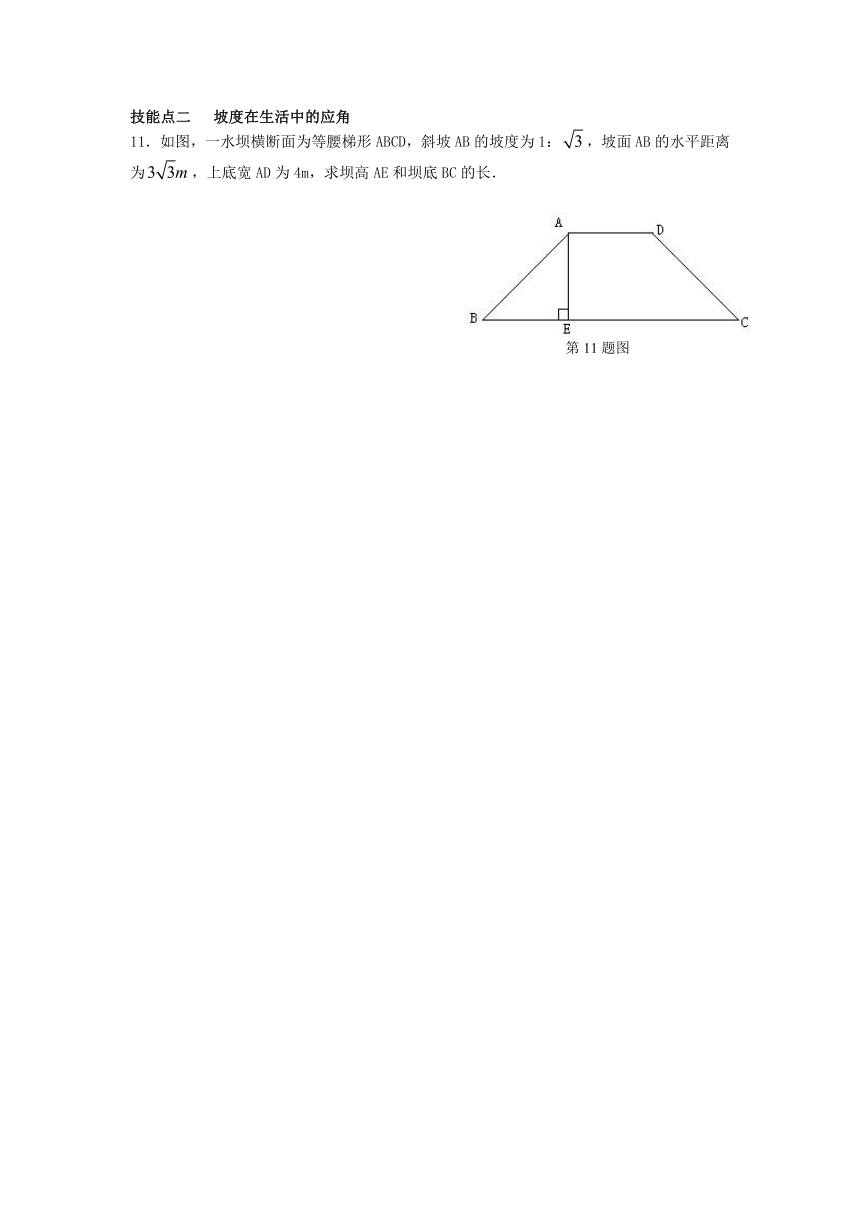
11.如图,一水坝横断面为等腰梯形ABCD,斜坡AB的坡度为1:,坡面AB的水平距离为,上底宽AD为4m,求坝高AE和坝底BC的长.
第2课时 正弦与余弦
知识点一 正弦的意义
1.如图在中,,则= = ,= =
2.在,若将各边长度都扩大为原来的2倍,则
∠A的正弦值 ( ).
A.扩大2倍 B.缩小2倍 C.扩大4倍 D.不变
3.在Rt△ABC中,∠C=90°,若AC=2BC,则sin A的值是 ( ) .
A. B.2 C. D.
4.已知在Rt△ABC中,∠C=90°,直角边AC是直角边BC的2倍,则sin∠A的值是 .
5.如图,角的顶点为O,它的一边在x轴的正半轴上,另一边OA上有一点P(3,4),则 .
知识点二 余弦的意义
6如图,在Rt△ABC中,∠C=90°,我们把锐角∠A的邻边b与斜边c的比叫做∠A的______,记作=_________,即cosA=______=_____.
7.在Rt△ABC中,∠C=90°,AB=5,BC=4,则cosA = .
8.在Rt△ABC中,∠C=90°,sinA=,则cosB的值等于( ).
A. B. C . D.
9.如图,在△中,,,是边上的高,,则 , .
10.如图,在Rt△ABC中,∠C=900,BC=6,sinA=,求cosA和tanB的值.
技能点一 利用网格求三角函数
11.在正方形网格中,的位置如图所示,则的值为( )
A. B. C. D.
技能点二 利用三角函数解决实际问题
12.如图,,,,,求 和点到直线的距离.
、
24.2锐角的三角函数
第1课时 、、的三角函数值
知识点一 、、的三角函数值
1. , , .
2.计算sin45°的结果等于( ).
A. B.1 C. D.
3.计算4sin60°-3tan30°的值为( ).
A. B.2 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 ) C.3 D.0
4.点M(-sin60°,cos60°)关于x轴对称的点的坐标是( ).
A.() B.(-) C.(-,) D.(-,-)
5.如图是引拉线固定电线杆的示意图.已知:CD⊥AB,CDm,∠CAD=∠DBC=60°,则拉线AC的长是______m.
知识点二 由三角函数值求锐角的度数
6.在Rt△ABC中,∠C=90°,sinA=,则∠A= .
7.在Rt△ABC中,∠C=900,sinA=,则cosB的值为( ).
A.1 B. C. D.
8.在△ABC中,∠A、∠B都是锐角,且sinA=,cosB= eq \f(,2) ,则△ABC的形状是( ).
A.直角三角形 B.钝角三角形 C.锐角三角形 D.不能确定
9.锐角A满足2sin(A-15) 0=?则∠A= .
10.已知,且关于的方程HYPERLINK "http://www.21cnjy.com" \o "欢迎登陆21世纪教育网"的两根平方和为10,求的大小.
技能点 特殊三角函数值的计算
11.计算:sin30 ·cos30 -tan30 = (结果保留根号)
12.计算:(1)
(2)
第2课时 三角函数之间的关系
知识点一 互余的两个锐角的正弦、余弦值的关系
1.已知为锐角,则 ; .
2.在中,,,则的值为( )
A. B. C. D.
3.在中,,下列式子一定成立的是( )
A. B.
C. D.
4.如果,那么= .
5.为直角三角形的一个锐角,若,求和的值.
知识点二 互余的两个锐角的正切值的关系
6.在中,,= ,若,则 .
7.若,则锐角等于( )
A. B. C. D.
8.已知,则= .
9.计算:= .
10.设和均为锐角,,且,求的值.
技能点 由特殊角的三角函数关系推导一般三角函数关系
11.如图,在中,BC、AC、AB三边的长分别为、、,则,,,我们不难发现:,…,试探求、、之间存在的一般关系,并说明理由.
12.阅读下面的材料,再回答问题
三角函数中,常用公式,求的值,即,请你用公式:,求的值.
第3课时 一般锐角三角函数值
知识点一 利用计算器求锐角三角函数
1.用计算器求按键顺序为:先按 ,再按 ,然后按 即可;求的按键顺序为:先按 ,再按 ,其次按 ,再按 ,其次按 ,最后按 .
2.用科学记数器求cos130的值,以下按键顺序正确的是( ).
A. cos 13 B. cos 2ndF 13
C. 13 cos D. 13 cos 2ndF
3.计算:sin20°- cos20°的值是( )(保留四个有效数字).
A.-0.5976 B.0.5976 C.-0.5977 D.0.5977
4.用计算器计算:cos36.32°=________.(结果保留四个有效数字) .
5.用计算器计算,结果保留四位有效数字:
sin51030/+cos49050/-tan46010/.
知识点二 已知三角函数求角度的方法
6.已知锐角A满足,利用计算器求的按键顺序为:先按 ,再按
,然后按 ,最后按 .结果要想以度、分、秒为单位显示,则再按 +
键即可.
7.已知sina=0.6031,则锐角a的度数是( )
A.3705/20// B.3708/30// C.3705/32// D.3706/40//
8.已知tanA=0.3600,利用计算器求出锐角A的值约为 .(精确到度)
9.在中,,的值是方程的根,则的度数为
.
10.已知A为锐角,求满足下列条件的A角(精确到0.1):
(1)sinA=0.9816;(2)cosA=0.8607.
技能点:利用三角函数的增减性比较大小
11.cos550和sin360的的大小关系是( )
A.cos550>sin360 B.cos550<sin360 C.cos550=sin360 D.不能确定
12.如果,那么锐角的范围大约是( )
A.00<<300 B.300<<450 C.450<<600 D.600<<900
13.比较下列三角函数值的大小:sin400 cos400.
14.(1)如图1、图2,锐角的正弦值和余弦值都随着锐角的确定而确定,变化而变化.试探索随着锐角度数的增大,它的正弦值和余弦值变化规律.
(2)根据你探索到的规律,试比较、、、、这些锐角的正弦值的大小和余弦值的大小.
(3)比较大小(在空格处填写“<”,或“>”,或“=”号).
若,则 ;若,则 ;
若,则 .
24.3解直角三角形及其应用
第1课时 直角三角形的边角关系
知识点一 已知两条边解直角三角形
1.在中,,AC=3,BC=,则AB= , ,
.
2.在中,,若AB=2,BC=,则的值为( ).
A. B. C. D.
3.已知梯形ABCD中,腰BC长为2,梯形对角线BD垂直平分AC,若梯形的高是,则∠CAB等于( )
A.30° B.60° C.45° D.以上都不对
4.如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,,有下列结论:(1)DE=3cm;(2)EB=1cm;.其中正确的个数为( ).
A.3个 B.2个 C.1个 D.0个
5.在中,,若,,那么 .
知识点二 已知一条边和一个锐角解直角三角形
6.在中,,,BC=4,则AB= ,斜边上的高为 .
7.如图,小明为了测量其所在位置A点到河对岸B点之间的距离,沿着与AB垂直的方向走了m米,到达点C,测得∠ACB=,那么AB等于( )
A. m·sin米 B.m·tan米 C. m·cos米 D.米
8.如图,一架梯子斜靠在墙上,若梯子底端到墙的距离AC=3米,cos∠BAC=,则梯子长AB = 米.
9.如图,在把易拉罐中的水倒入一个圆水杯的过程中,若水杯中的水在点与易拉罐刚好接触,则此时水杯中的水深为( )
A. B. C. D.
10.在△ABC中,AB=8,∠ABC=30°,AC=5,则BC=__________.
技能点 直角三角形的应用
11.已知等腰三角形一腰上的高为1,且这条高与底的夹角的正弦值为,求该三角形的面积.
12.已知在等腰梯形ABCD中,对角线AC与底边AB的夹角为300,且AC⊥BC,若腰BC=2,请你求出梯形ABCD的面积.
第2课时 仰角、俯角问题
知识点一 与仰角、俯角有关的问题
1.如图,在进行高度测量时,视线与水平线所成的角中,当视线在水平线上方时叫做 ;当视线在水平线下方时叫做 .
2.身高相同的三个小朋友甲,乙,丙放风筝,他们放出的线长分别为300m,250m,200m,线与地面所成的角度分别为30°,45°,60°(假设风筝线是拉直的),则三人所放风筝( ).
A.甲的最高 B.乙的最高 C.乙的最低 D.丙的最高
3.如图,河对岸有古塔AB.小明在C处测得塔顶A的仰角为α,向塔前进m到达D,在D处测得A的仰角为β,则塔高是 m.
4.小明站在A处放风筝,风筝飞到C处时的线长为20m,这时测得∠CBD=600,若牵引底端B离地面1.5m,求此时风筝离地面高度. (计算结果精确到0.1m,)
知识点二 与坡度有关的问题
5.如图,坡面的铅直高度()和水平长度()的比叫做坡面的坡度(或坡比),记作,即 ,坡面与水平面的夹角叫做坡角,记作,有= ,显然,坡度越大,坡角就越大,坡面就越陡.
6.一段公路的坡度为1︰3,某人沿这段公路路面前进100米,那么他上升的最大高度是 .
7.如图,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4m.如果在坡度为0.75的山坡上种树,也要求株距为4m,那么相邻两树间的坡面距离为( ).
A.5m B.6m C.7m D.8m
8.某校为了筹备校园艺术节,要在通往舞台的台阶上铺上红色地毯.如果地毯的宽度恰好与台阶的宽度一致,台阶的侧面如图所示,台阶的坡角为,,台阶的高为2米,那么请你帮忙算一算需要 米长的地毯恰好能铺好台阶.(结果精确到,取,)
技能点 利用仰角、俯角的概念解决实际问题
9.如图,为了对我市城区省级文物保护对象-—高AC约42米的天然塔进行保护性维修,工人要在塔顶A和塔底所在地面上的B处之间拉一根铁丝,在BC上的点D处测得塔顶的仰角α为43°(测倾器DE高1.6米,A,E,B三点在同一条直线上).求∠BAC的度数和铁丝AB的长.(接头部分的长度忽略不计,结果精确到0.1米.sin43°≈0.68,tan43°≈0.93)
10.为庆祝建国六十三周年,某校教学楼上悬挂着宣传条幅DC,小丽同学在点A处,测得条幅顶端D的仰角为30°,再向条幅方向前进10m后, 又在点B处测得条幅顶端D的仰角为45°,已知测点A、B和C离地面高度都为1.44米,求条幅顶端D点距离地面的高度.(计算结果精确到0.1m, 参考数据:.)
第3课时 方位角问题
知识点一 与方位角有关的问题
1.如图,B点在A点的南偏西 或 ;A点在B点的北偏东 或
.
2.如图,小明从A地沿北偏东方向走m到B地,再从B地向正南方向走200m到C地,此时小明离A地 m .
3.两座灯塔A和B与海洋观测站的距离相等,灯塔A在观测站的北偏东40°,灯塔B在观测站的南偏东60°,那么灯塔A在灯塔B的( ).
A.北偏东10° B.南偏东10° C.北偏西10° D.南偏西20°
4.小明同学在东西方向的沿江大道A处,测得江中灯塔P在北偏东60°方向上,在A处正东400米的B处,测得江中灯塔P在北偏东30°方向上,则灯塔P到沿江大道的距离为___________米.
5.如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处东500m的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC= m.
(用根号表示)
技能点一 利用方位角解决与航海、航空有关的实际问题
6.如图,客轮在海上以30km/h的速度由向航行,在处测得灯塔 的方位角为北偏东,测得处的方位角为南偏东,航行1小时后到达处,在处测得的方位角为北偏东,则到的距离是( ).
A.km B.km C.km D.km
7.如图,一艘轮船以每小时20海里的速度沿正北方向航行,在A处测得灯塔C在北偏西30°方向,轮船航行2小时后到达B处,在B处测得灯塔C在北偏西60°方向.当轮船到达灯塔C的正东方向的D处时,求此时轮船与灯塔C的距离.(结果保留根号)
技能点二 解决底部不能到达的测量问题
8.燕尾槽的横断面是等腰梯形.如图是一燕尾槽的横断面,其中燕尾角是,外口宽是16,燕尾槽的深度是6,求它的里口宽(精确到0.1).
9.某电视发射塔BC,为稳固塔身,周围拉有钢丝地锚线(如图线段AB),若AB=60m,并且AB与地面成45°角,欲升高发射塔的高度到CB/,同时原地锚线仍使用,若塔升高后使地锚线与地面成60°角,求电视发射塔升高了多少米?(即BB/的高度)(精确到0.01m).
第4课时 方案设计问题
知识点 坡度、坡角
1.如图所示,铁路的路基横断面是等腰梯形,斜坡的坡度为,坡面 的水平宽度为,基面宽为,则 , , .
2.河堤的横断面如图所示,堤高,迎水斜坡的长为,那么斜坡的坡度是( )
A. B. C. D.
3.如图,水库大坝的横断面是梯形,坝顶宽6m,坝高24m,斜坡的坡角 为,斜坡的坡角的正切值为,则坡底的长为( )
A.42m B.m C.m D.m
4.有一水库大坝的横截面是梯形(如图①),为水库的水面,点在上,某课题小组在老师的带领下想测量水的深度,他们测得背水坡的长为12米,迎水坡上的长为2米,求水深.(精确到0.1米,)
技能点 确定方案的合理性
5.如图所示,.两城市相距,现计划在这两座城市间修建一条高速公路(即线段),经测量,森林保护中心在城市的北偏东和城市的北偏西的方向上,已知森林保护区的范围在以点为圆心,为半径的圆形区域内,请问计划修建的这条高速公路会不会穿越保护区,为什么?(参考数据:)
6.我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,如图所示.,斜坡米,坡角,为防夏季因瀑雨引发山体滑坡,保障安全,学校决定对山坡进行改造.经地质人员勘测,当坡角不超过时,可确保山体不滑坡,改造时保持坡脚不动,从坡顶沿削进到处,问至少是多少米(结果保留根号)?
7.如果某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B处,经16小时的航行到到,到达后必须立即卸货,此时接到气象部门通知,一台风中心以40海里/小时的速度由A向北偏西方向移动,距台风中心200海里的区域均受到影响.
(1)B处是否会受到台风的影响?说明理由;
(2)若受台风影响,受影响的时间有多长?
(3)为避免受到台风影响,该船在多少小时内卸完货?
24章复习
1.在Rt△ABC中,∠C=900,cosA= ,则tanA等于( ).
A. B. C. D.24
2.小敏同学遇到了这样一道题:tan(α+10°)=1,你猜想锐角α的度数应是( ).
A.50° B.40° C.30° D.20°
3.在△ABC中,若tanA=1,sinB=,你认为最确切的判断是( ).
A.△ABC是等腰三角形 B.△ABC是等腰直角三角形
C.△ABC是直角三角形 D.△ABC是一般锐角三角形
4.小强和小明去测量一座古塔的高度(如图),他们在离古塔60米的A处,用测角仪器得塔顶的仰角为30°,已知测角仪器高AD=1.5米,则古塔BE的高为( ).
A.(20-1.5)米 B.(20+1.5)米 C.31.5 D.28.5
5.由山顶A望地面C、D两点的俯角分别为450、300,若CD=100m,则山高AB等于( ).
A.100m B.50m C.50m D.50(+1)m
6.计算:= .
7.直线与x轴正方向的夹角为,则= .
8.三角形在正方形网格纸中的位置如图所示,则sinα的值是 .
9.如图,坡角为的斜坡上两树间的水平距离AC为,则两树间的坡面距离AB为
10.一等腰梯形,下底长4m,高2cm,底角的余弦为,则上底长 m,腰长 m.
11.如图,在△中,∠=90°,sin=,=15,求△的周长和tan的值.
12.如图,在△ABC中,∠C=90 ,∠B=30 ,AD是∠BAC的平分线,BD=4,求AD的长.
13.如图,小明用一块有一个锐角为的直角三角板测量树高,已知小明离树的距离为4m,DE为1.68m,那么这棵树大约有多高?(精确到0.1m)
14.(2010·大连)如图,一艘海轮位于灯塔C的北偏东30°方向,距离灯塔80海里的A处,海轮沿正南方向匀速航行一段时间后,到达位于灯塔C的东南方向上的B处.
(1)求灯塔C到航线AB的距离;
(2)若海轮的速度为20海里/时,求海轮从A处到B处所用的时间(结果精确到0.1小时)
(参考数据:,)
15.一艘渔船在A处观测到东北方向有一小岛C,已知小岛C周围4.8海里范围内是水产养殖场.渔船沿北偏东30°方向航行10海里到达B处,在B处测得小岛C在北偏东60°方向,这时渔船改变航线向正东(即BD)方向航行,这艘渔船是否有进入养殖场的危险?
第24章解直角三角形
24.1锐角的三角函数
第1课时 正切
1. 2.A 3.B 4. 5.
6.坡度 坡比 7. 8.25 9.:1 10.A 11.坝高AE和坝底BC的长分别为3m、
第2课时 正弦与余弦
1. 2D 3.C 4. 5. 6.余弦 7 8.B 9. 10. 11.B 12. 点B到直线MC的距离为
24.2锐角的三角函数
第1课时 、、的三角函数值
1. 2.B 3.A 4.B 5.6 6. 7.C
8.A 9. 10. 11. 12.(1) (2)
第2课时 三角函数之间的关系
1. 2.C 3.D 4. 5. 6.1 3 7.C 8. 9.1 10.
11. 理由略
12.
第3课时 一般锐角三角函数值
1. 16 = 12 DMS 30 DMS 15 = 2.A
3.C 4.0.8057 5.0.3860 6.2ndf 0.9187 = 2ndf DMS
7.C 8. 9. 10.(1) (2) 11B 12.B
13. 14.(1)正弦值随着角度的增大而增大,余弦值随着角度的增大而减小;
(2);HYPERLINK "http://www.21cnjy.com" \o "欢迎登陆21世纪教育网" (3)若时,,若时,,若时,.
24.3解直角三角形及其应用
第1课时 直角三角形的边角关系
1.6 2.B 3.B 4.A 5. 6.8 7.B
8.4 9.C 10.或 11. 12.
第2课时 仰角、俯角问题
1.仰角 俯角 2.B 3. 4.18.8m. 5.
6. 7.A 8.5.5 9.因为BC∥EF,所以∠AEF=∠B=43°,又∠ACB=90°,所以∠BAC=90°-43°=47°,在Rt△ABC中,sinB==,所以AB=42÷sin43°≈42÷0.68≈61.8(米).因而∠BAC=47°,铁丝的长度是61.8米.
10.在Rt△BCD中, ,∴.在Rt△ACD中, ,∴.∴.∴.
∴(m). ∴条幅顶端D点距离地面的高度为(m).
第3课时 方位角问题
1. 西偏南 东偏北 2.100 3.C 4.
5. 6.D 7.轮船与灯塔C的距离为海里 8.作,垂足分别为,,在中,,∴ =.∴(cm).答:燕尾槽的里口宽约为24.4cm. 9.解:在Rt△ACB中,因为∠BAC=450,AB=60m,所以BC=AB·sin∠BAC=60×sin450=30(m).在Rt△A/B/C中,A/B/=60m,∠B/A/C=600,所以B/C=A/B/·sin600=60×(m).所以电视塔升高的高度:BB/=B/C-BC
第4课时 方案设计问题
1.3 () 2.C 3.A 4.提示:过A、D点作于于过作于 易得,即水深约为6.7米 5.提示:过P点作PH⊥AB于H点,易得PH=,所以会穿越保护区 6.提示:过B、E点分别作BG⊥AD于G点,EH⊥AD于H点,易证AG=20m,AH=m,所以BE至少为 7.(1)过B点作BH⊥AC交AC于点H,得BH=160<200,所以受到台风的影响;(2)6小时;(3)小时
24章复习
1.A 2.D 3.B 4.B 5.D 6.2 7. 8. 9.
101 2.5 11.的周长为36; 12. 13.4.0m 14.(1)灯塔C到AB的距离为40海里;(2)海轮从A处到B处所用的时间约为5.5小时.
15.过点C作CE⊥BD,垂足为E,∴CE∥GB∥FA.
∴∠BCE=∠GBC=60°.∠ACE=∠FAC=45°.
∴∠BCA=∠BCE-∠ACE=60°-45°=15°.
又∠BAC=∠FAC-∠FAB=45°-30°=15°,
∴∠BCA=∠BAC.∴BC=AB=10.
在Rt△BCE中,CE=BC·cos∠BCE=BC·cos60°=10×=5(海里).
∵5海里>4.8海里,∴渔船没有进入养殖场的危险.
A
B
C
D
第1题图
A
第4题图
B
D
M
N
C
·
·
A
C
B
D
第5题图
第6题图
第10题图
第11题图
第5题图
A
C
B
a
c
b
第1题图
A
B
D
C
第9题图
第6题图
第10题图
第11题图
C
A
B
M
第12题图
第5题图
A
C
图2
图1
A
B
C
第8题图
A
B
C
m
第7题图
第4题图
8cm
10cm
P
圆水杯
易拉罐
第9题图
第11题图
第12题图
第5题图
第5题图
第1题图
A
C
B
第8题图
第7题图
第9题图
第10题图
第2题图
P
A
B
C
30°
60°
北
第5题图
第1题图
北
东
第6题图
第7题图
第8题图
A/
A
C
B
B/
第9题图
一个坡面的铅直高度为,水平宽度为,则坡度 .设坡角为,则= ,
越大,坡角 ,坡面就 .
知识精梳理
A
D
C
F
E
B
第1题图
第3题图
第2题图
第4题图
第5题图
第6题图
第7题图
A
B
C
第9题图
第8题图
第4题图
第11题图
第12题图
第12题图
第13题图
第15题图
24.1锐角的三角函数
第1课时 正切
知识点一 正切的意义
1.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,
①tanA= = ;
②tanB= = ;
③tan∠ACD= ;
④tan∠BCD= .
2.在Rt△中,,若三角形的各边都扩大3倍,则的数值( ).
A.没有变化 B.扩大了3倍 C.缩小到 D.不能确定
3.在Rt△中,,,,则边的长为( ).
A. B. C. D.
4.如图,正方形ABCD的边长为4,点M在边DC上,M、N 两点关于对角线AC对称,若DM=1,则tan∠ADN= .
5.如图,在中,,于,若,,请你求出的值.
知识点一 坡度与坡角
6.正切常用来描述坡面的坡度,如图,坡面的铅直高度和水平宽度的比叫做坡面的 (或 ),记作,即 .
7.已知一个斜坡的长为10米,高度为8米,则坡度为 .
8.小敏沿着直坡度i=1:的山坡向上走了50m,这时他离地面______m.
9.有一拦水坝的横断面是等腰梯形,它的上底长为6米,下底长为10米,高为米,那么此拦水坝斜坡的坡度为 .
技能点一 求实际问题中的正切值
10.为测量如图所示上山坡道的倾斜度,小明测得图中所示的数据(单位:米),则该坡道倾斜角α的正切值是
A. B.4 C. D.
技能点二 坡度在生活中的应角
11.如图,一水坝横断面为等腰梯形ABCD,斜坡AB的坡度为1:,坡面AB的水平距离为,上底宽AD为4m,求坝高AE和坝底BC的长.
第2课时 正弦与余弦
知识点一 正弦的意义
1.如图在中,,则= = ,= =
2.在,若将各边长度都扩大为原来的2倍,则
∠A的正弦值 ( ).
A.扩大2倍 B.缩小2倍 C.扩大4倍 D.不变
3.在Rt△ABC中,∠C=90°,若AC=2BC,则sin A的值是 ( ) .
A. B.2 C. D.
4.已知在Rt△ABC中,∠C=90°,直角边AC是直角边BC的2倍,则sin∠A的值是 .
5.如图,角的顶点为O,它的一边在x轴的正半轴上,另一边OA上有一点P(3,4),则 .
知识点二 余弦的意义
6如图,在Rt△ABC中,∠C=90°,我们把锐角∠A的邻边b与斜边c的比叫做∠A的______,记作=_________,即cosA=______=_____.
7.在Rt△ABC中,∠C=90°,AB=5,BC=4,则cosA = .
8.在Rt△ABC中,∠C=90°,sinA=,则cosB的值等于( ).
A. B. C . D.
9.如图,在△中,,,是边上的高,,则 , .
10.如图,在Rt△ABC中,∠C=900,BC=6,sinA=,求cosA和tanB的值.
技能点一 利用网格求三角函数
11.在正方形网格中,的位置如图所示,则的值为( )
A. B. C. D.
技能点二 利用三角函数解决实际问题
12.如图,,,,,求 和点到直线的距离.
、
24.2锐角的三角函数
第1课时 、、的三角函数值
知识点一 、、的三角函数值
1. , , .
2.计算sin45°的结果等于( ).
A. B.1 C. D.
3.计算4sin60°-3tan30°的值为( ).
A. B.2 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 ) C.3 D.0
4.点M(-sin60°,cos60°)关于x轴对称的点的坐标是( ).
A.() B.(-) C.(-,) D.(-,-)
5.如图是引拉线固定电线杆的示意图.已知:CD⊥AB,CDm,∠CAD=∠DBC=60°,则拉线AC的长是______m.
知识点二 由三角函数值求锐角的度数
6.在Rt△ABC中,∠C=90°,sinA=,则∠A= .
7.在Rt△ABC中,∠C=900,sinA=,则cosB的值为( ).
A.1 B. C. D.
8.在△ABC中,∠A、∠B都是锐角,且sinA=,cosB= eq \f(,2) ,则△ABC的形状是( ).
A.直角三角形 B.钝角三角形 C.锐角三角形 D.不能确定
9.锐角A满足2sin(A-15) 0=?则∠A= .
10.已知,且关于的方程HYPERLINK "http://www.21cnjy.com" \o "欢迎登陆21世纪教育网"的两根平方和为10,求的大小.
技能点 特殊三角函数值的计算
11.计算:sin30 ·cos30 -tan30 = (结果保留根号)
12.计算:(1)
(2)
第2课时 三角函数之间的关系
知识点一 互余的两个锐角的正弦、余弦值的关系
1.已知为锐角,则 ; .
2.在中,,,则的值为( )
A. B. C. D.
3.在中,,下列式子一定成立的是( )
A. B.
C. D.
4.如果,那么= .
5.为直角三角形的一个锐角,若,求和的值.
知识点二 互余的两个锐角的正切值的关系
6.在中,,= ,若,则 .
7.若,则锐角等于( )
A. B. C. D.
8.已知,则= .
9.计算:= .
10.设和均为锐角,,且,求的值.
技能点 由特殊角的三角函数关系推导一般三角函数关系
11.如图,在中,BC、AC、AB三边的长分别为、、,则,,,我们不难发现:,…,试探求、、之间存在的一般关系,并说明理由.
12.阅读下面的材料,再回答问题
三角函数中,常用公式,求的值,即,请你用公式:,求的值.
第3课时 一般锐角三角函数值
知识点一 利用计算器求锐角三角函数
1.用计算器求按键顺序为:先按 ,再按 ,然后按 即可;求的按键顺序为:先按 ,再按 ,其次按 ,再按 ,其次按 ,最后按 .
2.用科学记数器求cos130的值,以下按键顺序正确的是( ).
A. cos 13 B. cos 2ndF 13
C. 13 cos D. 13 cos 2ndF
3.计算:sin20°- cos20°的值是( )(保留四个有效数字).
A.-0.5976 B.0.5976 C.-0.5977 D.0.5977
4.用计算器计算:cos36.32°=________.(结果保留四个有效数字) .
5.用计算器计算,结果保留四位有效数字:
sin51030/+cos49050/-tan46010/.
知识点二 已知三角函数求角度的方法
6.已知锐角A满足,利用计算器求的按键顺序为:先按 ,再按
,然后按 ,最后按 .结果要想以度、分、秒为单位显示,则再按 +
键即可.
7.已知sina=0.6031,则锐角a的度数是( )
A.3705/20// B.3708/30// C.3705/32// D.3706/40//
8.已知tanA=0.3600,利用计算器求出锐角A的值约为 .(精确到度)
9.在中,,的值是方程的根,则的度数为
.
10.已知A为锐角,求满足下列条件的A角(精确到0.1):
(1)sinA=0.9816;(2)cosA=0.8607.
技能点:利用三角函数的增减性比较大小
11.cos550和sin360的的大小关系是( )
A.cos550>sin360 B.cos550<sin360 C.cos550=sin360 D.不能确定
12.如果,那么锐角的范围大约是( )
A.00<<300 B.300<<450 C.450<<600 D.600<<900
13.比较下列三角函数值的大小:sin400 cos400.
14.(1)如图1、图2,锐角的正弦值和余弦值都随着锐角的确定而确定,变化而变化.试探索随着锐角度数的增大,它的正弦值和余弦值变化规律.
(2)根据你探索到的规律,试比较、、、、这些锐角的正弦值的大小和余弦值的大小.
(3)比较大小(在空格处填写“<”,或“>”,或“=”号).
若,则 ;若,则 ;
若,则 .
24.3解直角三角形及其应用
第1课时 直角三角形的边角关系
知识点一 已知两条边解直角三角形
1.在中,,AC=3,BC=,则AB= , ,
.
2.在中,,若AB=2,BC=,则的值为( ).
A. B. C. D.
3.已知梯形ABCD中,腰BC长为2,梯形对角线BD垂直平分AC,若梯形的高是,则∠CAB等于( )
A.30° B.60° C.45° D.以上都不对
4.如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,,有下列结论:(1)DE=3cm;(2)EB=1cm;.其中正确的个数为( ).
A.3个 B.2个 C.1个 D.0个
5.在中,,若,,那么 .
知识点二 已知一条边和一个锐角解直角三角形
6.在中,,,BC=4,则AB= ,斜边上的高为 .
7.如图,小明为了测量其所在位置A点到河对岸B点之间的距离,沿着与AB垂直的方向走了m米,到达点C,测得∠ACB=,那么AB等于( )
A. m·sin米 B.m·tan米 C. m·cos米 D.米
8.如图,一架梯子斜靠在墙上,若梯子底端到墙的距离AC=3米,cos∠BAC=,则梯子长AB = 米.
9.如图,在把易拉罐中的水倒入一个圆水杯的过程中,若水杯中的水在点与易拉罐刚好接触,则此时水杯中的水深为( )
A. B. C. D.
10.在△ABC中,AB=8,∠ABC=30°,AC=5,则BC=__________.
技能点 直角三角形的应用
11.已知等腰三角形一腰上的高为1,且这条高与底的夹角的正弦值为,求该三角形的面积.
12.已知在等腰梯形ABCD中,对角线AC与底边AB的夹角为300,且AC⊥BC,若腰BC=2,请你求出梯形ABCD的面积.
第2课时 仰角、俯角问题
知识点一 与仰角、俯角有关的问题
1.如图,在进行高度测量时,视线与水平线所成的角中,当视线在水平线上方时叫做 ;当视线在水平线下方时叫做 .
2.身高相同的三个小朋友甲,乙,丙放风筝,他们放出的线长分别为300m,250m,200m,线与地面所成的角度分别为30°,45°,60°(假设风筝线是拉直的),则三人所放风筝( ).
A.甲的最高 B.乙的最高 C.乙的最低 D.丙的最高
3.如图,河对岸有古塔AB.小明在C处测得塔顶A的仰角为α,向塔前进m到达D,在D处测得A的仰角为β,则塔高是 m.
4.小明站在A处放风筝,风筝飞到C处时的线长为20m,这时测得∠CBD=600,若牵引底端B离地面1.5m,求此时风筝离地面高度. (计算结果精确到0.1m,)
知识点二 与坡度有关的问题
5.如图,坡面的铅直高度()和水平长度()的比叫做坡面的坡度(或坡比),记作,即 ,坡面与水平面的夹角叫做坡角,记作,有= ,显然,坡度越大,坡角就越大,坡面就越陡.
6.一段公路的坡度为1︰3,某人沿这段公路路面前进100米,那么他上升的最大高度是 .
7.如图,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4m.如果在坡度为0.75的山坡上种树,也要求株距为4m,那么相邻两树间的坡面距离为( ).
A.5m B.6m C.7m D.8m
8.某校为了筹备校园艺术节,要在通往舞台的台阶上铺上红色地毯.如果地毯的宽度恰好与台阶的宽度一致,台阶的侧面如图所示,台阶的坡角为,,台阶的高为2米,那么请你帮忙算一算需要 米长的地毯恰好能铺好台阶.(结果精确到,取,)
技能点 利用仰角、俯角的概念解决实际问题
9.如图,为了对我市城区省级文物保护对象-—高AC约42米的天然塔进行保护性维修,工人要在塔顶A和塔底所在地面上的B处之间拉一根铁丝,在BC上的点D处测得塔顶的仰角α为43°(测倾器DE高1.6米,A,E,B三点在同一条直线上).求∠BAC的度数和铁丝AB的长.(接头部分的长度忽略不计,结果精确到0.1米.sin43°≈0.68,tan43°≈0.93)
10.为庆祝建国六十三周年,某校教学楼上悬挂着宣传条幅DC,小丽同学在点A处,测得条幅顶端D的仰角为30°,再向条幅方向前进10m后, 又在点B处测得条幅顶端D的仰角为45°,已知测点A、B和C离地面高度都为1.44米,求条幅顶端D点距离地面的高度.(计算结果精确到0.1m, 参考数据:.)
第3课时 方位角问题
知识点一 与方位角有关的问题
1.如图,B点在A点的南偏西 或 ;A点在B点的北偏东 或
.
2.如图,小明从A地沿北偏东方向走m到B地,再从B地向正南方向走200m到C地,此时小明离A地 m .
3.两座灯塔A和B与海洋观测站的距离相等,灯塔A在观测站的北偏东40°,灯塔B在观测站的南偏东60°,那么灯塔A在灯塔B的( ).
A.北偏东10° B.南偏东10° C.北偏西10° D.南偏西20°
4.小明同学在东西方向的沿江大道A处,测得江中灯塔P在北偏东60°方向上,在A处正东400米的B处,测得江中灯塔P在北偏东30°方向上,则灯塔P到沿江大道的距离为___________米.
5.如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处东500m的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC= m.
(用根号表示)
技能点一 利用方位角解决与航海、航空有关的实际问题
6.如图,客轮在海上以30km/h的速度由向航行,在处测得灯塔 的方位角为北偏东,测得处的方位角为南偏东,航行1小时后到达处,在处测得的方位角为北偏东,则到的距离是( ).
A.km B.km C.km D.km
7.如图,一艘轮船以每小时20海里的速度沿正北方向航行,在A处测得灯塔C在北偏西30°方向,轮船航行2小时后到达B处,在B处测得灯塔C在北偏西60°方向.当轮船到达灯塔C的正东方向的D处时,求此时轮船与灯塔C的距离.(结果保留根号)
技能点二 解决底部不能到达的测量问题
8.燕尾槽的横断面是等腰梯形.如图是一燕尾槽的横断面,其中燕尾角是,外口宽是16,燕尾槽的深度是6,求它的里口宽(精确到0.1).
9.某电视发射塔BC,为稳固塔身,周围拉有钢丝地锚线(如图线段AB),若AB=60m,并且AB与地面成45°角,欲升高发射塔的高度到CB/,同时原地锚线仍使用,若塔升高后使地锚线与地面成60°角,求电视发射塔升高了多少米?(即BB/的高度)(精确到0.01m).
第4课时 方案设计问题
知识点 坡度、坡角
1.如图所示,铁路的路基横断面是等腰梯形,斜坡的坡度为,坡面 的水平宽度为,基面宽为,则 , , .
2.河堤的横断面如图所示,堤高,迎水斜坡的长为,那么斜坡的坡度是( )
A. B. C. D.
3.如图,水库大坝的横断面是梯形,坝顶宽6m,坝高24m,斜坡的坡角 为,斜坡的坡角的正切值为,则坡底的长为( )
A.42m B.m C.m D.m
4.有一水库大坝的横截面是梯形(如图①),为水库的水面,点在上,某课题小组在老师的带领下想测量水的深度,他们测得背水坡的长为12米,迎水坡上的长为2米,求水深.(精确到0.1米,)
技能点 确定方案的合理性
5.如图所示,.两城市相距,现计划在这两座城市间修建一条高速公路(即线段),经测量,森林保护中心在城市的北偏东和城市的北偏西的方向上,已知森林保护区的范围在以点为圆心,为半径的圆形区域内,请问计划修建的这条高速公路会不会穿越保护区,为什么?(参考数据:)
6.我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,如图所示.,斜坡米,坡角,为防夏季因瀑雨引发山体滑坡,保障安全,学校决定对山坡进行改造.经地质人员勘测,当坡角不超过时,可确保山体不滑坡,改造时保持坡脚不动,从坡顶沿削进到处,问至少是多少米(结果保留根号)?
7.如果某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B处,经16小时的航行到到,到达后必须立即卸货,此时接到气象部门通知,一台风中心以40海里/小时的速度由A向北偏西方向移动,距台风中心200海里的区域均受到影响.
(1)B处是否会受到台风的影响?说明理由;
(2)若受台风影响,受影响的时间有多长?
(3)为避免受到台风影响,该船在多少小时内卸完货?
24章复习
1.在Rt△ABC中,∠C=900,cosA= ,则tanA等于( ).
A. B. C. D.24
2.小敏同学遇到了这样一道题:tan(α+10°)=1,你猜想锐角α的度数应是( ).
A.50° B.40° C.30° D.20°
3.在△ABC中,若tanA=1,sinB=,你认为最确切的判断是( ).
A.△ABC是等腰三角形 B.△ABC是等腰直角三角形
C.△ABC是直角三角形 D.△ABC是一般锐角三角形
4.小强和小明去测量一座古塔的高度(如图),他们在离古塔60米的A处,用测角仪器得塔顶的仰角为30°,已知测角仪器高AD=1.5米,则古塔BE的高为( ).
A.(20-1.5)米 B.(20+1.5)米 C.31.5 D.28.5
5.由山顶A望地面C、D两点的俯角分别为450、300,若CD=100m,则山高AB等于( ).
A.100m B.50m C.50m D.50(+1)m
6.计算:= .
7.直线与x轴正方向的夹角为,则= .
8.三角形在正方形网格纸中的位置如图所示,则sinα的值是 .
9.如图,坡角为的斜坡上两树间的水平距离AC为,则两树间的坡面距离AB为
10.一等腰梯形,下底长4m,高2cm,底角的余弦为,则上底长 m,腰长 m.
11.如图,在△中,∠=90°,sin=,=15,求△的周长和tan的值.
12.如图,在△ABC中,∠C=90 ,∠B=30 ,AD是∠BAC的平分线,BD=4,求AD的长.
13.如图,小明用一块有一个锐角为的直角三角板测量树高,已知小明离树的距离为4m,DE为1.68m,那么这棵树大约有多高?(精确到0.1m)
14.(2010·大连)如图,一艘海轮位于灯塔C的北偏东30°方向,距离灯塔80海里的A处,海轮沿正南方向匀速航行一段时间后,到达位于灯塔C的东南方向上的B处.
(1)求灯塔C到航线AB的距离;
(2)若海轮的速度为20海里/时,求海轮从A处到B处所用的时间(结果精确到0.1小时)
(参考数据:,)
15.一艘渔船在A处观测到东北方向有一小岛C,已知小岛C周围4.8海里范围内是水产养殖场.渔船沿北偏东30°方向航行10海里到达B处,在B处测得小岛C在北偏东60°方向,这时渔船改变航线向正东(即BD)方向航行,这艘渔船是否有进入养殖场的危险?
第24章解直角三角形
24.1锐角的三角函数
第1课时 正切
1. 2.A 3.B 4. 5.
6.坡度 坡比 7. 8.25 9.:1 10.A 11.坝高AE和坝底BC的长分别为3m、
第2课时 正弦与余弦
1. 2D 3.C 4. 5. 6.余弦 7 8.B 9. 10. 11.B 12. 点B到直线MC的距离为
24.2锐角的三角函数
第1课时 、、的三角函数值
1. 2.B 3.A 4.B 5.6 6. 7.C
8.A 9. 10. 11. 12.(1) (2)
第2课时 三角函数之间的关系
1. 2.C 3.D 4. 5. 6.1 3 7.C 8. 9.1 10.
11. 理由略
12.
第3课时 一般锐角三角函数值
1. 16 = 12 DMS 30 DMS 15 = 2.A
3.C 4.0.8057 5.0.3860 6.2ndf 0.9187 = 2ndf DMS
7.C 8. 9. 10.(1) (2) 11B 12.B
13. 14.(1)正弦值随着角度的增大而增大,余弦值随着角度的增大而减小;
(2);HYPERLINK "http://www.21cnjy.com" \o "欢迎登陆21世纪教育网" (3)若时,,若时,,若时,.
24.3解直角三角形及其应用
第1课时 直角三角形的边角关系
1.6 2.B 3.B 4.A 5. 6.8 7.B
8.4 9.C 10.或 11. 12.
第2课时 仰角、俯角问题
1.仰角 俯角 2.B 3. 4.18.8m. 5.
6. 7.A 8.5.5 9.因为BC∥EF,所以∠AEF=∠B=43°,又∠ACB=90°,所以∠BAC=90°-43°=47°,在Rt△ABC中,sinB==,所以AB=42÷sin43°≈42÷0.68≈61.8(米).因而∠BAC=47°,铁丝的长度是61.8米.
10.在Rt△BCD中, ,∴.在Rt△ACD中, ,∴.∴.∴.
∴(m). ∴条幅顶端D点距离地面的高度为(m).
第3课时 方位角问题
1. 西偏南 东偏北 2.100 3.C 4.
5. 6.D 7.轮船与灯塔C的距离为海里 8.作,垂足分别为,,在中,,∴ =.∴(cm).答:燕尾槽的里口宽约为24.4cm. 9.解:在Rt△ACB中,因为∠BAC=450,AB=60m,所以BC=AB·sin∠BAC=60×sin450=30(m).在Rt△A/B/C中,A/B/=60m,∠B/A/C=600,所以B/C=A/B/·sin600=60×(m).所以电视塔升高的高度:BB/=B/C-BC
第4课时 方案设计问题
1.3 () 2.C 3.A 4.提示:过A、D点作于于过作于 易得,即水深约为6.7米 5.提示:过P点作PH⊥AB于H点,易得PH=,所以会穿越保护区 6.提示:过B、E点分别作BG⊥AD于G点,EH⊥AD于H点,易证AG=20m,AH=m,所以BE至少为 7.(1)过B点作BH⊥AC交AC于点H,得BH=160<200,所以受到台风的影响;(2)6小时;(3)小时
24章复习
1.A 2.D 3.B 4.B 5.D 6.2 7. 8. 9.
101 2.5 11.的周长为36; 12. 13.4.0m 14.(1)灯塔C到AB的距离为40海里;(2)海轮从A处到B处所用的时间约为5.5小时.
15.过点C作CE⊥BD,垂足为E,∴CE∥GB∥FA.
∴∠BCE=∠GBC=60°.∠ACE=∠FAC=45°.
∴∠BCA=∠BCE-∠ACE=60°-45°=15°.
又∠BAC=∠FAC-∠FAB=45°-30°=15°,
∴∠BCA=∠BAC.∴BC=AB=10.
在Rt△BCE中,CE=BC·cos∠BCE=BC·cos60°=10×=5(海里).
∵5海里>4.8海里,∴渔船没有进入养殖场的危险.
A
B
C
D
第1题图
A
第4题图
B
D
M
N
C
·
·
A
C
B
D
第5题图
第6题图
第10题图
第11题图
第5题图
A
C
B
a
c
b
第1题图
A
B
D
C
第9题图
第6题图
第10题图
第11题图
C
A
B
M
第12题图
第5题图
A
C
图2
图1
A
B
C
第8题图
A
B
C
m
第7题图
第4题图
8cm
10cm
P
圆水杯
易拉罐
第9题图
第11题图
第12题图
第5题图
第5题图
第1题图
A
C
B
第8题图
第7题图
第9题图
第10题图
第2题图
P
A
B
C
30°
60°
北
第5题图
第1题图
北
东
第6题图
第7题图
第8题图
A/
A
C
B
B/
第9题图
一个坡面的铅直高度为,水平宽度为,则坡度 .设坡角为,则= ,
越大,坡角 ,坡面就 .
知识精梳理
A
D
C
F
E
B
第1题图
第3题图
第2题图
第4题图
第5题图
第6题图
第7题图
A
B
C
第9题图
第8题图
第4题图
第11题图
第12题图
第12题图
第13题图
第15题图
