第二十八章 锐角三角函数全章复习
文档属性
| 名称 | 第二十八章 锐角三角函数全章复习 |  | |
| 格式 | zip | ||
| 文件大小 | 815.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-01-05 21:39:36 | ||
图片预览




文档简介
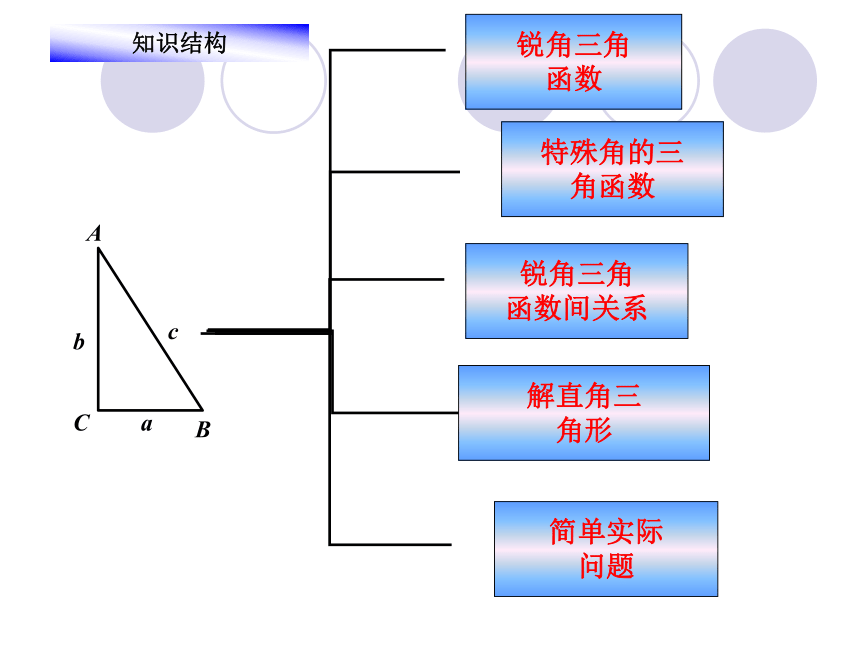
课件22张PPT。28.全章复习九年级下册C M Y C Z锐角三角
函数特殊角的三
角函数解直角三
角形简单实际
问题知识结构锐角三角
函数间关系自学指导一 回顾锐角三角函数的定义,
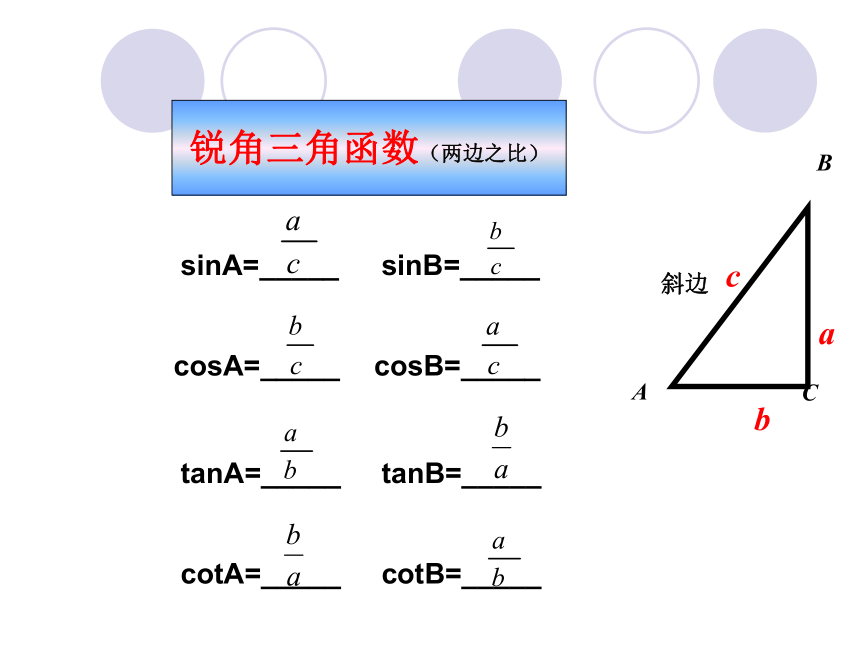
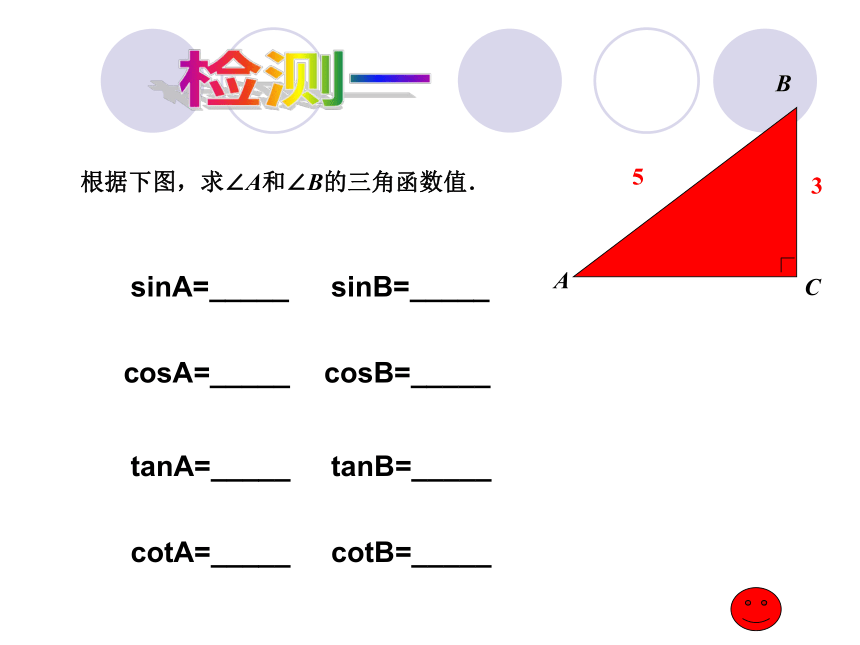
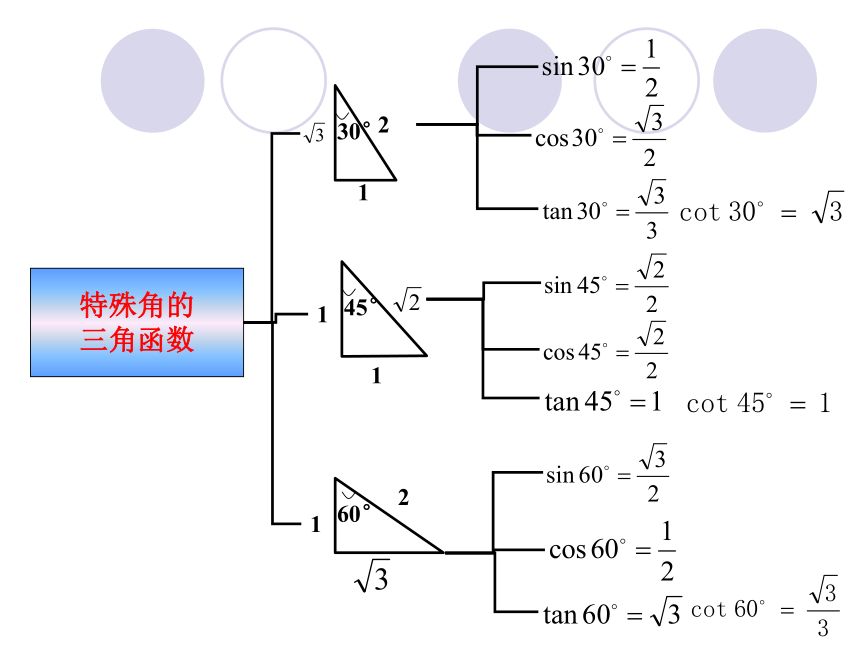
并会简单的运用.锐角三角函数(两边之比)ABCcab斜边sinA=_____ cosA=_____ tanA=_____ cotA=_____ sinB=_____ cosB=_____ tanB=_____ cotB=_____ AC35B根据下图,求∠A和∠B的三角函数值.sinA=_____ cosA=_____ tanA=_____ cotA=_____ sinB=_____ cosB=_____ tanB=_____ cotB=_____ 检测一自学指导二 掌握特殊角的三角函数值,并能熟练运用.特殊角的
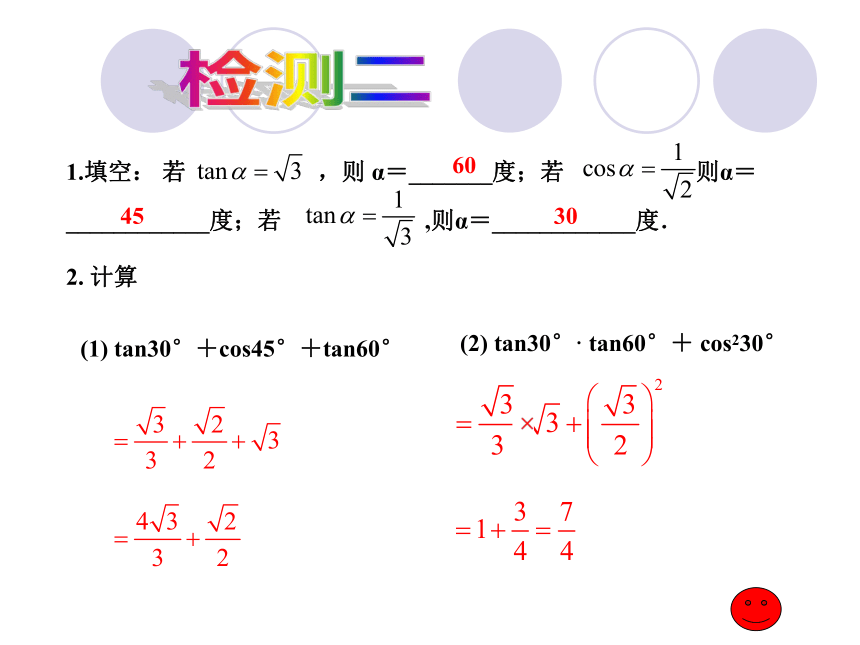
三角函数检测二1.填空: 若 ,则 α=_______度;若 则α=____________度;若 ,则α=____________度.604530(1) tan30°+cos45°+tan60°(2) tan30°· tan60°+ cos230°2. 计算 掌握锐角三角函数间的关系,
并利用关系简便运算.自学指导三锐角三角函数间的关系ABCcab斜边sinA=COSB cosA= sinB tanA= cotB cotA= tanB sin2A+cos2A=1 tanA×cotA=1 1、互为余角三角函数间的关系
2、同角三角函数间的关系平方关系:倒数关系:商数关系:1. 若 且∠B=90°- ∠A,则sinB=_______2. 在△ABC中, ∠A、 ∠B都是锐角,且sinA=cosB,那么 △ABC一定是____________三角形.检测三3.sin2350+cos2350=________
sin2240+sin2660=_________4.tan440×tan450×tan460=_____ 掌握直角三角形的边角关系,并利用边角关系解直角三角形.自学指导四(2)两锐角之间的关系:∠A+∠B=90°(3)边角之间的关系:(1)三边之间的关系: (勾股定理)ABabcC在解直角三角形的过程中,一般要用到
下面一些关系:知识回顾1、如图在Rt △ABC中∠A=300,
AC=10,解这个直角三角形.检测四2、在 △ABC中∠A=300,
tanB=1/3,BC= ,求AB的长。?自学指导五 利用解直角三角形,解决简单的实际问题.
简单实
际问题数学模型直角三角形等腰梯形组合图形等腰三角形构建解作高转化为直角三角形解 某校教学楼后面紧邻着一个土坡,坡上面是一块平地,如图, BC∥AD ,斜坡 AB 为22m ,坡角 ∠BAD=600,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.经地质人员勘测,当坡角不超过 450时,可确保山体不滑坡.
求改造前坡顶与地面的距离BE的长.
为确保安全,学校计划改造时保持坡脚A 不动,坡顶 B 沿BC削进到 F点处,问BF 至少是多少米?检测五(2)过F作FG⊥AD于G,连结AF.G在RT △FGA中, ∵∠FAG=450作业:P101 5.6.8.谢谢指导
函数特殊角的三
角函数解直角三
角形简单实际
问题知识结构锐角三角
函数间关系自学指导一 回顾锐角三角函数的定义,
并会简单的运用.锐角三角函数(两边之比)ABCcab斜边sinA=_____ cosA=_____ tanA=_____ cotA=_____ sinB=_____ cosB=_____ tanB=_____ cotB=_____ AC35B根据下图,求∠A和∠B的三角函数值.sinA=_____ cosA=_____ tanA=_____ cotA=_____ sinB=_____ cosB=_____ tanB=_____ cotB=_____ 检测一自学指导二 掌握特殊角的三角函数值,并能熟练运用.特殊角的
三角函数检测二1.填空: 若 ,则 α=_______度;若 则α=____________度;若 ,则α=____________度.604530(1) tan30°+cos45°+tan60°(2) tan30°· tan60°+ cos230°2. 计算 掌握锐角三角函数间的关系,
并利用关系简便运算.自学指导三锐角三角函数间的关系ABCcab斜边sinA=COSB cosA= sinB tanA= cotB cotA= tanB sin2A+cos2A=1 tanA×cotA=1 1、互为余角三角函数间的关系
2、同角三角函数间的关系平方关系:倒数关系:商数关系:1. 若 且∠B=90°- ∠A,则sinB=_______2. 在△ABC中, ∠A、 ∠B都是锐角,且sinA=cosB,那么 △ABC一定是____________三角形.检测三3.sin2350+cos2350=________
sin2240+sin2660=_________4.tan440×tan450×tan460=_____ 掌握直角三角形的边角关系,并利用边角关系解直角三角形.自学指导四(2)两锐角之间的关系:∠A+∠B=90°(3)边角之间的关系:(1)三边之间的关系: (勾股定理)ABabcC在解直角三角形的过程中,一般要用到
下面一些关系:知识回顾1、如图在Rt △ABC中∠A=300,
AC=10,解这个直角三角形.检测四2、在 △ABC中∠A=300,
tanB=1/3,BC= ,求AB的长。?自学指导五 利用解直角三角形,解决简单的实际问题.
简单实
际问题数学模型直角三角形等腰梯形组合图形等腰三角形构建解作高转化为直角三角形解 某校教学楼后面紧邻着一个土坡,坡上面是一块平地,如图, BC∥AD ,斜坡 AB 为22m ,坡角 ∠BAD=600,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.经地质人员勘测,当坡角不超过 450时,可确保山体不滑坡.
求改造前坡顶与地面的距离BE的长.
为确保安全,学校计划改造时保持坡脚A 不动,坡顶 B 沿BC削进到 F点处,问BF 至少是多少米?检测五(2)过F作FG⊥AD于G,连结AF.G在RT △FGA中, ∵∠FAG=450作业:P101 5.6.8.谢谢指导
