【新课标】6.3从统计图中分析数据的集中趋势 课件(共25张PPT)
文档属性
| 名称 | 【新课标】6.3从统计图中分析数据的集中趋势 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-12 11:14:51 | ||
图片预览







文档简介
(共25张PPT)
6.3从统计图中分析数据的集中趋势
北师大版八年级上册
教学目标
1.经历从统计图分析数据集中趋势的活动,建立数据直觉,发展几何直观;
2.能从条形统计图、扇形统计图等统计图中获取信息,求出或估计相关数据的平均数、中位数、众数.
情境导入
平均数、中位数和众数都是用来代表一组数据的集中趋势特征.
平均数反映一组数据的平均水平;
中位数反映一组数据的中等水平;
众数反映一组数据的多数水平.
新知讲解
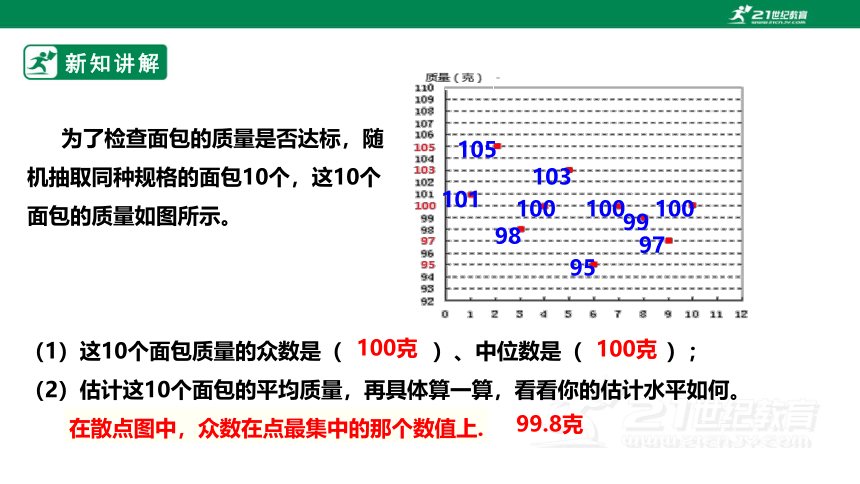
为了检查面包的质量是否达标,随机抽取同种规格的面包10个,这10个面包的质量如图所示。
(1)这10个面包质量的众数是( )、中位数是( );
(2)估计这10个面包的平均质量,再具体算一算,看看你的估计水平如何。
100克
100克
99.8克
101
105
98
100
103
100
100
99
97
95
在散点图中,众数在点最集中的那个数值上.
归纳总结
众数: ;
中位数: ;
平均数:____________________________.
同一水平线上出现次数最多的数据
折线图上,从上到下(或从下到上)处于中间点所对应的数
可以用中位数与众数估测平均数,具体计算时可以以这个数为基准用简便算法求平均数
在折线统计图中,可以怎样求一组数据的众数、中位数、平均数?
议一议
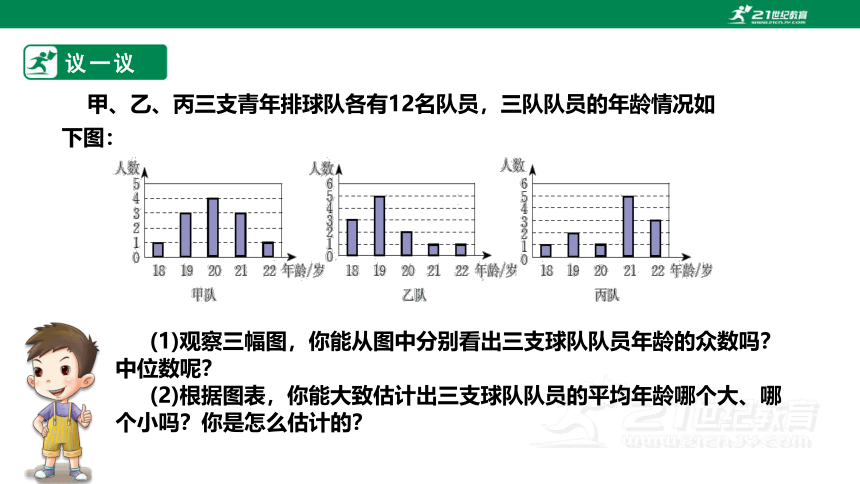
甲、乙、丙三支青年排球队各有12名队员,三队队员的年龄情况如下图:
(1)观察三幅图,你能从图中分别看出三支球队队员年龄的众数吗?中位数呢?
(2)根据图表,你能大致估计出三支球队队员的平均年龄哪个大、哪个小吗?你是怎么估计的?
议一议
解:(1) 从图中可以看出:
甲队队员年龄的众数是_____,中位数是_____;
乙队队员年龄的众数是_____,中位数是_____;
丙队队员年龄的众数是_____,中位数是_____.
20岁
20岁
19岁
19岁
21岁
21岁
(2)因为丙队队员年龄大的人数较多,所以估计丙队队员平均年龄最大,而乙队队员年龄大的人数较少,所以乙队队员平均年龄最小.
议一议
解:甲:(18×1+19×3+20×4+21×3+22×1)÷12=20(岁);
乙: (18×3+19×5+20×2+21×1+22×1)÷12 ≈ 19.3(岁);
丙: (18×1+19×2+20×1+21×5+22×3)÷12≈ 20.6(岁).
(3)计算出三支球队队员的平均年龄,看看你的估计是否准确.
归纳总结
条形统计图中,柱子最高的是众数;找中位数要先排大小顺序;还可以用数据的中位数与众数估测其平均数.
想一想
(1)在这20位同学中,本学期计划购买课外书的花费的众数是多少?
小明调查了班级里20位同学本学期计划购买课外书的花费情况,并将结果绘制成了下面的统计图:
(2)计算这20位同学计划购买课外书的平均花费是多少?你是怎么计算的?
想一想
解:(1)50元在扇形图中所占面积最大,所以众数为50元.
(2)平均花费=100×10%+80×25%+50×40%+30×20%+20×5%=57(元).
归纳总结
在上面的问题中,如果不知道调查的总人数,你还能求平均数吗
因为扇形统计图能看出部分在总体中所占的百分比,所以利用扇形统计图更容易看出数据的众数;利用加权平均数的求法可以求出数据的平均数.
典例精析
例:某地连续统计了10天日最高气温,并绘制成如图所示的扇形统计图.
(1)这10天中,日最高气温的众数是多少?
(2)计算这10天日最高气温的平均值。
解:(1)根据扇形统计图,35℃占的比例最大,因此日平均气温的众数是35℃.
(2)这10天日最高气温的平均值是:
32×10%+33×20%+34×20%+35×30%+36×20%
=34.3(℃)
归纳总结
扇形统计图中
众数:为扇形面积最大的数据;
中位数:按顺序,看相应百分比,第50%与51%两个数据的平均数;
平均数:可以利用加权平均数进行计算.
课堂练习
1.如图是某射击手5次射击成绩的折线图,根据图中信息,这组数据的众数、中位数各是多少( )
A.7环,9环 B.7环,8环
C.8环,9环 D.8环,10环
B
课堂练习
2.如图是某校中的40名学生一周的体育锻炼时间绘制成的条形统计图,根据统计图提供的数据,该校40名学生一周参加体育锻炼时间(单位: h)的众数与中位数分别是( )
A. 8h,9h B. 8h,8h C. 9h,8h D. 10h,9h
A
课堂练习
3.如图是某中学男田径队队员年龄结构条形统计图 ,根据图中信息解答下列问题:
(1)田径队共有______人。
(2)该队队员年龄的众数是____ _;中位数是______ .
(3)该队队员的平均年龄是_____ _.
队员人数
15岁
16岁
17岁
18岁
0
1
2
3
4
年龄
10
17岁
17岁
16.9岁
课堂练习
4.如图是根据今年某校八年级学生体育考试跳绳的成绩绘制成的统计图.如果该校八年级共有200名学生参加了这项跳绳考试,根据该统计图给出的信息可得这些同学跳绳考试的平均成绩为________.
175.5
课堂练习
5.
请你根据以上提供的信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)所抽取学生对数学学习喜欢程度的众数是_________;
(3)若该校七年级共有960名学生,请你估算该年级学生中对数学学习“不太喜欢”的约有多少名.
比较喜欢
课堂练习
解:(1)由题意可得,
调查的学生有30÷25%=120(名),
选B的学生有120-18-30-6=66(名),
B所占的百分比是66÷120×100%=55%,
D所占的百分比是6÷120×100%=5%,
故补全的条形统计图与扇形统计图如图所示:
(3)960×25%= 240(名).
答:该年级学生中对数学学习“不太喜欢”的约有240名.
课堂总结
从统计图分析数据的集中趋势
折线统计图
条形统计图
扇形统计图
板书设计
从统计图分析数据的集中趋势
1. 统计图的种类:扇形图、条形图、折线图、表格
2. 从统计图中分析中位数,众数,平均数
作业布置
教材147页习题第1,4,5题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
6.3从统计图中分析数据的集中趋势
北师大版八年级上册
教学目标
1.经历从统计图分析数据集中趋势的活动,建立数据直觉,发展几何直观;
2.能从条形统计图、扇形统计图等统计图中获取信息,求出或估计相关数据的平均数、中位数、众数.
情境导入
平均数、中位数和众数都是用来代表一组数据的集中趋势特征.
平均数反映一组数据的平均水平;
中位数反映一组数据的中等水平;
众数反映一组数据的多数水平.
新知讲解
为了检查面包的质量是否达标,随机抽取同种规格的面包10个,这10个面包的质量如图所示。
(1)这10个面包质量的众数是( )、中位数是( );
(2)估计这10个面包的平均质量,再具体算一算,看看你的估计水平如何。
100克
100克
99.8克
101
105
98
100
103
100
100
99
97
95
在散点图中,众数在点最集中的那个数值上.
归纳总结
众数: ;
中位数: ;
平均数:____________________________.
同一水平线上出现次数最多的数据
折线图上,从上到下(或从下到上)处于中间点所对应的数
可以用中位数与众数估测平均数,具体计算时可以以这个数为基准用简便算法求平均数
在折线统计图中,可以怎样求一组数据的众数、中位数、平均数?
议一议
甲、乙、丙三支青年排球队各有12名队员,三队队员的年龄情况如下图:
(1)观察三幅图,你能从图中分别看出三支球队队员年龄的众数吗?中位数呢?
(2)根据图表,你能大致估计出三支球队队员的平均年龄哪个大、哪个小吗?你是怎么估计的?
议一议
解:(1) 从图中可以看出:
甲队队员年龄的众数是_____,中位数是_____;
乙队队员年龄的众数是_____,中位数是_____;
丙队队员年龄的众数是_____,中位数是_____.
20岁
20岁
19岁
19岁
21岁
21岁
(2)因为丙队队员年龄大的人数较多,所以估计丙队队员平均年龄最大,而乙队队员年龄大的人数较少,所以乙队队员平均年龄最小.
议一议
解:甲:(18×1+19×3+20×4+21×3+22×1)÷12=20(岁);
乙: (18×3+19×5+20×2+21×1+22×1)÷12 ≈ 19.3(岁);
丙: (18×1+19×2+20×1+21×5+22×3)÷12≈ 20.6(岁).
(3)计算出三支球队队员的平均年龄,看看你的估计是否准确.
归纳总结
条形统计图中,柱子最高的是众数;找中位数要先排大小顺序;还可以用数据的中位数与众数估测其平均数.
想一想
(1)在这20位同学中,本学期计划购买课外书的花费的众数是多少?
小明调查了班级里20位同学本学期计划购买课外书的花费情况,并将结果绘制成了下面的统计图:
(2)计算这20位同学计划购买课外书的平均花费是多少?你是怎么计算的?
想一想
解:(1)50元在扇形图中所占面积最大,所以众数为50元.
(2)平均花费=100×10%+80×25%+50×40%+30×20%+20×5%=57(元).
归纳总结
在上面的问题中,如果不知道调查的总人数,你还能求平均数吗
因为扇形统计图能看出部分在总体中所占的百分比,所以利用扇形统计图更容易看出数据的众数;利用加权平均数的求法可以求出数据的平均数.
典例精析
例:某地连续统计了10天日最高气温,并绘制成如图所示的扇形统计图.
(1)这10天中,日最高气温的众数是多少?
(2)计算这10天日最高气温的平均值。
解:(1)根据扇形统计图,35℃占的比例最大,因此日平均气温的众数是35℃.
(2)这10天日最高气温的平均值是:
32×10%+33×20%+34×20%+35×30%+36×20%
=34.3(℃)
归纳总结
扇形统计图中
众数:为扇形面积最大的数据;
中位数:按顺序,看相应百分比,第50%与51%两个数据的平均数;
平均数:可以利用加权平均数进行计算.
课堂练习
1.如图是某射击手5次射击成绩的折线图,根据图中信息,这组数据的众数、中位数各是多少( )
A.7环,9环 B.7环,8环
C.8环,9环 D.8环,10环
B
课堂练习
2.如图是某校中的40名学生一周的体育锻炼时间绘制成的条形统计图,根据统计图提供的数据,该校40名学生一周参加体育锻炼时间(单位: h)的众数与中位数分别是( )
A. 8h,9h B. 8h,8h C. 9h,8h D. 10h,9h
A
课堂练习
3.如图是某中学男田径队队员年龄结构条形统计图 ,根据图中信息解答下列问题:
(1)田径队共有______人。
(2)该队队员年龄的众数是____ _;中位数是______ .
(3)该队队员的平均年龄是_____ _.
队员人数
15岁
16岁
17岁
18岁
0
1
2
3
4
年龄
10
17岁
17岁
16.9岁
课堂练习
4.如图是根据今年某校八年级学生体育考试跳绳的成绩绘制成的统计图.如果该校八年级共有200名学生参加了这项跳绳考试,根据该统计图给出的信息可得这些同学跳绳考试的平均成绩为________.
175.5
课堂练习
5.
请你根据以上提供的信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)所抽取学生对数学学习喜欢程度的众数是_________;
(3)若该校七年级共有960名学生,请你估算该年级学生中对数学学习“不太喜欢”的约有多少名.
比较喜欢
课堂练习
解:(1)由题意可得,
调查的学生有30÷25%=120(名),
选B的学生有120-18-30-6=66(名),
B所占的百分比是66÷120×100%=55%,
D所占的百分比是6÷120×100%=5%,
故补全的条形统计图与扇形统计图如图所示:
(3)960×25%= 240(名).
答:该年级学生中对数学学习“不太喜欢”的约有240名.
课堂总结
从统计图分析数据的集中趋势
折线统计图
条形统计图
扇形统计图
板书设计
从统计图分析数据的集中趋势
1. 统计图的种类:扇形图、条形图、折线图、表格
2. 从统计图中分析中位数,众数,平均数
作业布置
教材147页习题第1,4,5题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
