广西地区人教版2021、2022两年数学中考真题、模拟题分类选编—几何图形初步 练习题(含解析)
文档属性
| 名称 | 广西地区人教版2021、2022两年数学中考真题、模拟题分类选编—几何图形初步 练习题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 373.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-10 11:32:47 | ||
图片预览



文档简介
广西地区2021、2022两年数学中考真题、模拟题分类选编—几何图形初步 练习题
一、单选题
1.(2022·广西柳州·中考真题)如图,从学校A到书店B有①、②、③、④四条路线,其中最短的路线是( )
A.① B.② C.③ D.④
2.(2022·广西柳州·中考真题)如图,将矩形绕着它的一边所在的直线l旋转一周,可以得到的立体图形是( )
A. B. C. D.
3.(2021·广西百色·中考真题)已知∠α=25°30′,则它的余角为( )
A.25°30′ B.64°30′ C.74°30′ D.154°30′
4.(2021·广西百色·中考真题)下列展开图中,不是正方体展开图的是( )
A. B.
C. D.
5.(2021·广西贺州·中考真题)下列四个几何体中,左视图为圆的是( )
A. B. C. D.
6.(2022·广西梧州·二模)下列在立体图形中,它的侧面展开图是扇形的是( )
A.正方体 B.长方体 C.圆柱 D.圆锥
7.(2022·广西河池·三模)已知,则它的余角为( )
A.20° B.60° C.70° D.160°
8.(2022·广西梧州·一模)如图是某个几何体的侧面展开图,这个几何体可能是( ).
A.圆柱 B.圆锥 C.三棱锥 D.三棱柱
9.(2022·广西贺州·一模)已知,,则∠BOC的度数为( )
A.78° B.42° C.78°或42° D.102°或48°
10.(2022·广西贺州·一模)下面四个图形中,是三棱锥的平面展开图的是( )
A. B.
C. D.
11.(2022·广西南宁·一模)下图是一个几何体的展开图,该几何体是( )
A.圆柱体 B.四棱柱 C.三棱锥 D.圆锥体
12.(2022·广西柳州·二模)下列图形中,可能是圆锥侧面展开图的是( )
A. B.
C. D.
13.(2022·广西柳州·二模)如图,已知四条线段,,,中的一条与挡板另一侧的线段在同一直线上,请借助直尺判断该线段是( )
A. B.
C. D.
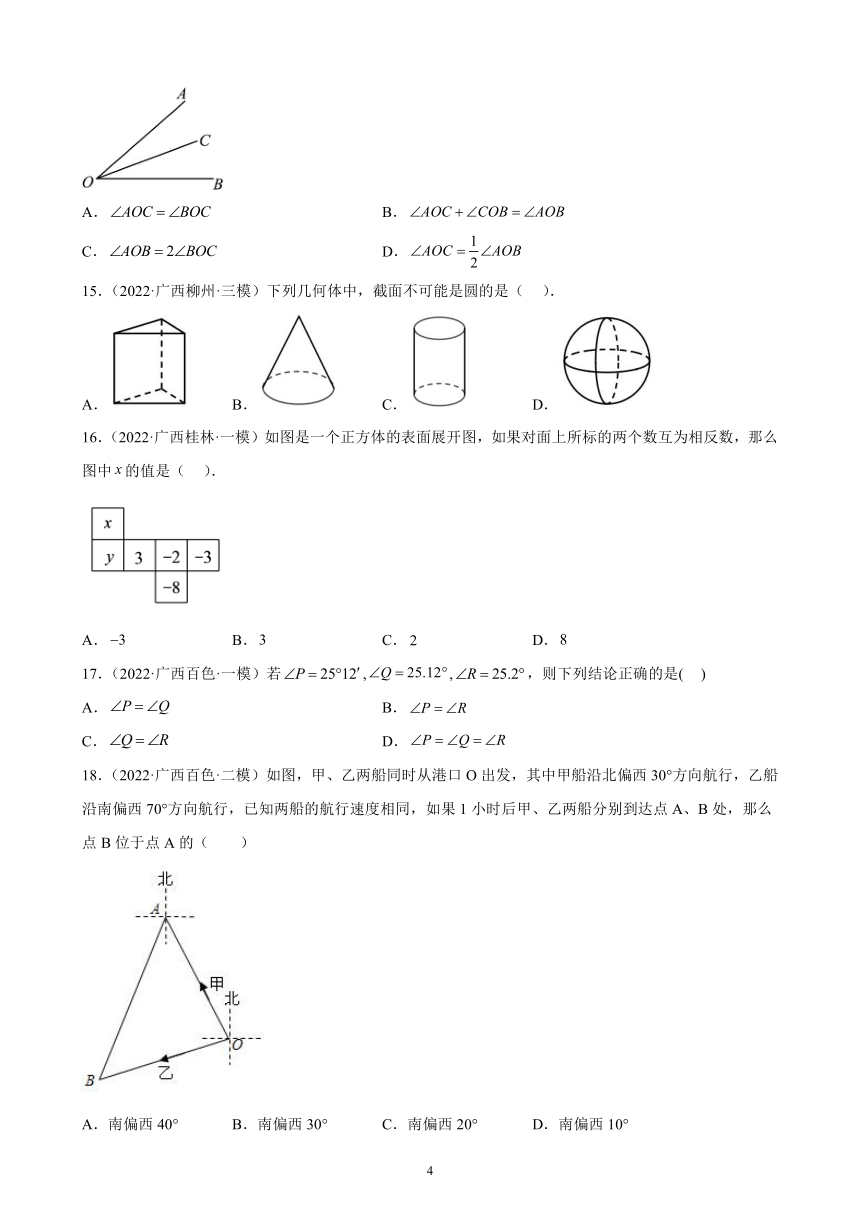
14.(2022·广西百色·二模)如图,OC为内的一条射线,下列条件中不能确定OC平分的是( )
A. B.
C. D.
15.(2022·广西柳州·三模)下列几何体中,截面不可能是圆的是( ).
A. B. C. D.
16.(2022·广西桂林·一模)如图是一个正方体的表面展开图,如果对面上所标的两个数互为相反数,那么图中的值是( ).
A. B. C. D.
17.(2022·广西百色·一模)若,,,则下列结论正确的是( )
A. B.
C. D.
18.(2022·广西百色·二模)如图,甲、乙两船同时从港口O出发,其中甲船沿北偏西30°方向航行,乙船沿南偏西70°方向航行,已知两船的航行速度相同,如果1小时后甲、乙两船分别到达点A、B处,那么点B位于点A的( )
A.南偏西40° B.南偏西30° C.南偏西20° D.南偏西10°
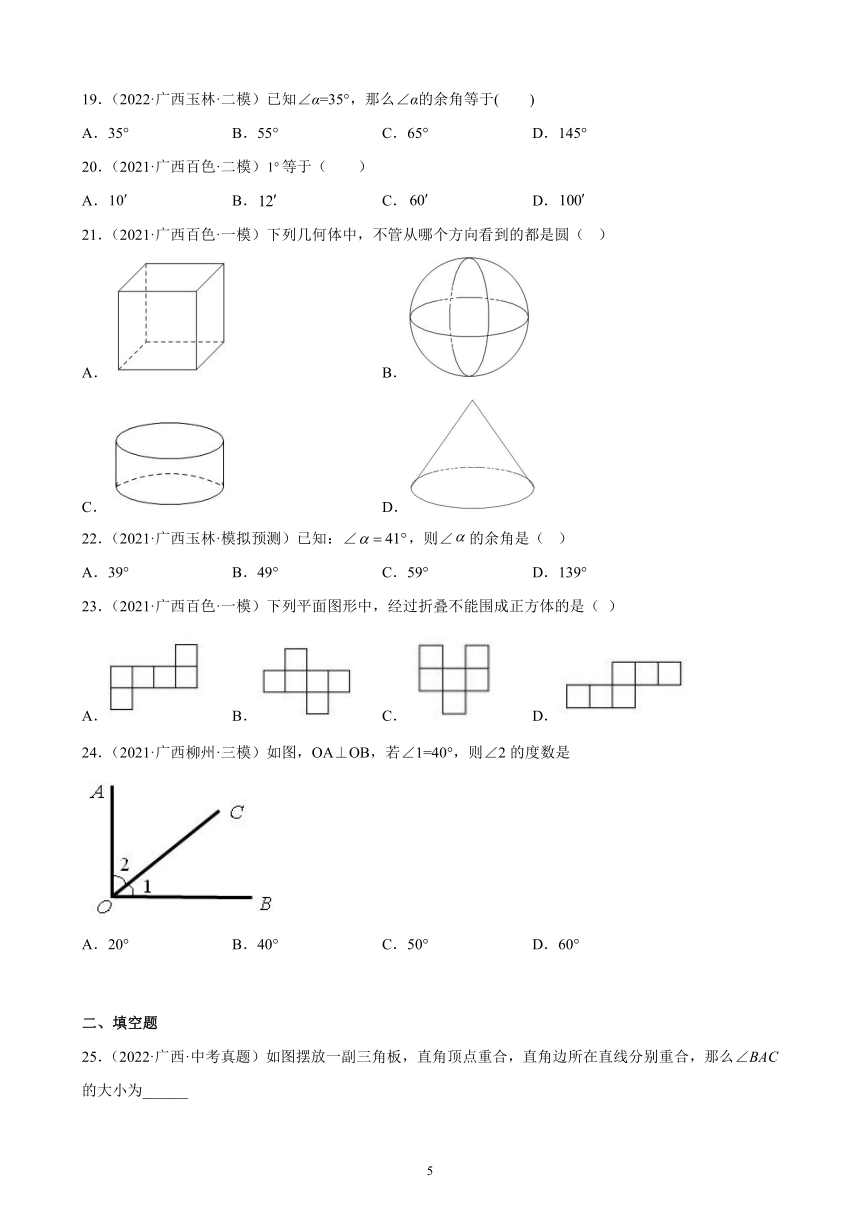
19.(2022·广西玉林·二模)已知∠α=35°,那么∠α的余角等于( )
A.35° B.55° C.65° D.145°
20.(2021·广西百色·二模)等于( )
A. B. C. D.
21.(2021·广西百色·一模)下列几何体中,不管从哪个方向看到的都是圆( )
A. B.
C. D.
22.(2021·广西玉林·模拟预测)已知:∠,则∠的余角是( )
A.39° B.49° C.59° D.139°
23.(2021·广西百色·一模)下列平面图形中,经过折叠不能围成正方体的是( )
A. B. C. D.
24.(2021·广西柳州·三模)如图,OA⊥OB,若∠1=40°,则∠2的度数是
A.20° B.40° C.50° D.60°
二、填空题
25.(2022·广西·中考真题)如图摆放一副三角板,直角顶点重合,直角边所在直线分别重合,那么∠BAC的大小为______
26.(2022·广西桂林·中考真题)如图,点C是线段AB的中点,若AC=2cm,则AB=_____cm.
27.(2022·广西玉林·中考真题)已知∠α=60°,则∠α的余角等于____度.
28.(2022·广西·柳城县教育局教研室一模)如图,点D是线段AB的中点,C是线段AD的中点,若AB=8cm,则CD=___cm.
29.(2022·广西百色·一模)一个几何体由若干个大小相同的小立方块搭成,从左面和上面看到的平面图形如图所示,则搭成这个几何体的小立方块的个数为_____.
30.(2021·广西·柳城县教育局教研室一模)如图所示,建筑工人砌墙时,经常在两个墙角的位置分别插一根小桩,然后拉一条直的参照线,可以这样做的数学道理_____________.
参考答案:
1.B
【解析】根据两点之间线段最短进行解答即可.
解:∵两点之间线段最短,
∴从学校A到书店B有①、②、③、④四条路线中,最短的路线是②,故B正确.
故选:B.
本题主要考查了两点之间线段最短,解题的关键是熟练掌握两点之间所有连线中,线段最短.
2.B
【解析】根据面动成体:一个长方形绕着它的一条边所在的直线旋转一周后所得到的立体图形是圆柱,据此判断即可.
解:由题意可知:
一个长方形绕着它的一条边所在的直线旋转一周后所得到的立体图形是圆柱.
故选:B
本题考查了圆柱的概念和面动成体,属于应知应会题型,熟练掌握基础知识是解题关键.
3.B
【解析】根据互为余角相加等于以及度分秒的进率计算即可.
解:∵∠α=25°30′,
∴它的余角为,
故选:B.
本题主要考查余角的性质以及度分秒的计算,熟知度分秒的进率为60是解题的关键.
4.D
【解析】根据正方体的展开图特征解题.
解:A.是正方体的展开图,故A不符合题意;
B.是正方体的展开图,故B不符合题意;
C.是正方体的展开图,故C不符合题意;
D.不是正方体的展开图,故D符合题意,
故选:D.
本题考查正方体的展开图,熟知正方体的11种展开图是解题关键.
5.A
【解析】根据三视图的法则可得出答案.
解:左视图为从左往右看得到的视图,
A.球的左视图是圆,
B.圆柱的左视图是长方形,
C.圆锥的左视图是等腰三角形,
D.圆台的左视图是等腰梯形,
故符合题意的选项是A.
错因分析 较容易题.失分原因是不会判断常见几何体的三视图.
6.D
【解析】根据各个图形的侧面展开图求得正确答案,即可.
解:A选项,正方体的侧面展开图不是扇形,不符合题意;
B选项,长方体的侧面展开图不是扇形,不符合题意;
C选项,圆柱的侧面展开图是长方形或正方形,不是扇形,不符合题意;
D选项,圆锥的侧面展开图是扇形,符合题意.
故选:D.
本题考查了几何体的侧面展开图,熟悉选项中每个图形的侧面展开图是解题的关键.
7.C
【解析】根据两角和为90度,这两角互为余角求解即可.
解:∠α的余角=90°-∠α=90°-20°=70°,
故选:C.
本题考查余角的概念,熟练掌握余角的概念是解题的关键.
8.B
【解析】由图可知展开侧面为扇形,则该几何体为圆锥.
解:该几何体的侧面展开图是扇形,所以这个几何体可能是圆锥,
故选:B.
此题主要考查几何体的展开图,熟记几何体的侧面展开图是解题的关键.
9.C
【解析】分两种情况讨论,即①当 在 内部时,②当在外部时,先根据题意画图,然后根据角的和差关系计算即可.
解:①如图,当在内部时,
;
②如图,当在外部时,
;
综上所述,的度数为和.
故选:C.
本题考查了几何图形中角的计算,解题的关键是注意分两种情况讨论.
10.B
【解析】根据三棱锥的四个面都是三角形,还要能围成一个立体图形,进而分析得出即可.
解:A.此图形可以围成三棱柱,故此选项不符合题意;
B.此图形可以围成三棱锥,故此选项符合题意;
C.此图形可以围成四棱锥,故此选项不符合题意;
D.无法围成立体图形,故此选项不符合题意.
故选:B.
本题主要考查了几何体的展开图,注意几何体的形状特点进而分析才行.
11.D
【解析】根据侧面展开图为一个扇形,底面是一个圆,所以该几何体是圆锥.
解:由题意,
∵侧面展开图为一个扇形,底面是一个圆,
∴该几何体是圆锥体;
故选:D
本题考查了几何体的侧面展开图,从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
12.B
【解析】根据圆锥的侧面展开图为扇形判断即可.
解:由圆锥的侧面展开图是扇形可知选B,
故选:B.
本题主要考查圆锥侧面展开图的形状,题型比较简单,熟知关于圆锥的知识点是解决本题的关键.
13.A
【解析】根据直线的特征,经过两点有一直线并且只有一条直线即可判断.
解:设线段m与挡板的交点为A,a、b、c、d与挡板的交点分别为B,C,D,E,
连结AB、AC、AD、AE,
根据直线的特征经过两点有且只有一条直线,
利用直尺可确定线段a与m在同一直线上,
故选择A.
本题考查直线的特征,掌握直线的特征是解题关键.
14.B
【解析】根据角平分线的定义判断即可.
解:A选项.∵∠AOC=∠BOC
∴OC平分∠AOB.
所以A选项正确,不符合题意;
B选项.∵∠AOC+∠COB=∠AOB,
∴OC不一定平分∠AOB.
所以B选项不正确,符合题意;
C选项.∵∠AOB=2∠BOC,
∴OC平分∠AOB.
所以C选项正确,不符合题意;
D.∵,
∴OC平分∠AOB.
所以D选项正确,不符合题意.
故选:B.
本题考查了角平分线的定义,解决本题的关键是掌握角平分线的定义.
15.A
【解析】根据一个几何体有几个面,则截面最多是几边形,由于棱柱没有曲面,所以用一个平面去截棱柱,截面不可能是圆.
A选项:截面不可能是圆,故正确;;
B选项:截面可能是圆,故错误;
C选项:截面可能是圆,故错误;
D选项:截面一定是圆,故错误.
故选A.
本题考查截面的定义,同时应注意的是截面的形状随截法的不同而改变,若一个几何体有几个面,则截面最多是几边形.
16.D
【解析】根据正方体平面展开图的特征得出每个相对面,再由相对面上的两个数互为相反数可得出x的值.
解:“3”与“-3”相对,“y”与“-2”相对,“x”与“-8”相对, 故x=8,故选D.
本题主要考查了正方体相对面上的文字,解决本题的关键是要熟练掌握正方体展开图的特征.
17.B
【解析】根据小单位化大单位除以进率,可得答案.
解: ∠P=25°12′=25.2°,∠R=25.2°
所以B选项是正确的.
本题考查角的大小比较.关键是将单位统一,即度、分、秒的换算.
18.C
试题分析:由甲船沿北偏西30°方向航行,乙船沿南偏西70°方向航行,得出∠BOA的度数,由两船的航行速度相同,得出AO=BO,得出∠BAO=50°,以及求出∠BAD的度数,得出点B位于点A的方向,故本题选C.
点睛:本题主要考查的就是方位角的问题,属于中等难度题型.解决这个问题的关键就是要能够根据已知的条件得出各个角的度数,从而求出问题中所要求的角的度数.在解决这种类型的题目时,我们还要注意参照物是那个物体,就要以参照物为标注建立方位图,从而得出答案.
19.B
【解析】根据余角的定义:如果两个角的和等于90°(直角),就说这两个角互为余角计算.
解:∵∠α=35°,
∴它的余角等于90°﹣35°=55°.
故选B.
本题考查余角的概念,掌握概念正确计算是本题的解题关键.
20.C
【解析】根据度分秒之间的进制关系,进行计算即可.
解:;
故选C.
本题考查度分秒的计算.熟练掌握度分秒之间的进制关系,是解题的关键.
21.B
【解析】球体不管从哪个方向看到的都是圆,据此判断即可.
解:不管从哪个方向看到的都是圆的是球体,
故选:B.
本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.
22.B
【解析】直接根据余角的概念解答即可.
:根据余角的概念,这个角的余角为:90°-41°=49°.
故选:B.
本题考查了余角的概念:如果两个角的和等于90°,就说这两个角互为余角.
23.C
【解析】根据正方体展开图的常见形式作答即可.
解:由展开图可知:、、能围成正方体,故不符合题意;
、围成几何体时,有两个面重合,不能围成正方体,故符合题意.
故选:.
本题主要考查展开图折叠成几何体的知识点,注意只要有“田、凹”字格的展开图都不是正方体的表面展开图.
24.C
∵OA⊥OB,∴∠AOB=90°.
又∵∠1=40°,∴∠2=∠AOB-∠1=90°-40°=50°,
故选C.
25.135°##135度
【解析】根据三角板及其摆放位置可得,求解即可.
,
,
故答案为:135°.
本题考查了求一个角的补角,即两个角的和为180度时,这两个角互为补角,熟练掌握知识点是解题的关键.
26.4
【解析】根据中点的定义可得AB=2AC=4cm.
解:根据中点的定义可得:AB=2AC=2×2=4(cm),
故答案为:4.
本题主要考查中点的定义,熟知中点的定义是解题关键.
27.30
∵互余两角的和等于90°,
∴α的余角为:90°-60°=30°.
故答案为:30
28.2
【解析】由点D是线段AB的中点,C是线段AD的中点,可得,即可求得答案.
解:∵点D是线段AB的中点,
∴,
∵C是线段AD的中点,
∴,
∴,
故答案为:2.
本题主要考查线段的中点,熟练运用线段的中点求线段长是解题的关键.
29.4
【解析】根据左面看与上面看的图形,得到俯视图解答即可.
解:根据左视图和俯视图,这个几何体的底层有3个小正方体,
第二层有1个小正方体,
所以有个小正方体,
故答案为:4.
本题主要考查从不同方向看几何体,熟练掌握几何体的特征是解题的关键.
30.两点确定一条直线
【解析】根据两点确定一条直线判断即可;
经常在两个墙角的位置分别插一根小桩,然后拉一条直的参照线,可以这样做的数学道理两点确定一条直线;
故答案是两点确定一条直线.
本题主要考查了点与线的关系,准确判断是解题的关键.
一、单选题
1.(2022·广西柳州·中考真题)如图,从学校A到书店B有①、②、③、④四条路线,其中最短的路线是( )
A.① B.② C.③ D.④
2.(2022·广西柳州·中考真题)如图,将矩形绕着它的一边所在的直线l旋转一周,可以得到的立体图形是( )
A. B. C. D.
3.(2021·广西百色·中考真题)已知∠α=25°30′,则它的余角为( )
A.25°30′ B.64°30′ C.74°30′ D.154°30′
4.(2021·广西百色·中考真题)下列展开图中,不是正方体展开图的是( )
A. B.
C. D.
5.(2021·广西贺州·中考真题)下列四个几何体中,左视图为圆的是( )
A. B. C. D.
6.(2022·广西梧州·二模)下列在立体图形中,它的侧面展开图是扇形的是( )
A.正方体 B.长方体 C.圆柱 D.圆锥
7.(2022·广西河池·三模)已知,则它的余角为( )
A.20° B.60° C.70° D.160°
8.(2022·广西梧州·一模)如图是某个几何体的侧面展开图,这个几何体可能是( ).
A.圆柱 B.圆锥 C.三棱锥 D.三棱柱
9.(2022·广西贺州·一模)已知,,则∠BOC的度数为( )
A.78° B.42° C.78°或42° D.102°或48°
10.(2022·广西贺州·一模)下面四个图形中,是三棱锥的平面展开图的是( )
A. B.
C. D.
11.(2022·广西南宁·一模)下图是一个几何体的展开图,该几何体是( )
A.圆柱体 B.四棱柱 C.三棱锥 D.圆锥体
12.(2022·广西柳州·二模)下列图形中,可能是圆锥侧面展开图的是( )
A. B.
C. D.
13.(2022·广西柳州·二模)如图,已知四条线段,,,中的一条与挡板另一侧的线段在同一直线上,请借助直尺判断该线段是( )
A. B.
C. D.
14.(2022·广西百色·二模)如图,OC为内的一条射线,下列条件中不能确定OC平分的是( )
A. B.
C. D.
15.(2022·广西柳州·三模)下列几何体中,截面不可能是圆的是( ).
A. B. C. D.
16.(2022·广西桂林·一模)如图是一个正方体的表面展开图,如果对面上所标的两个数互为相反数,那么图中的值是( ).
A. B. C. D.
17.(2022·广西百色·一模)若,,,则下列结论正确的是( )
A. B.
C. D.
18.(2022·广西百色·二模)如图,甲、乙两船同时从港口O出发,其中甲船沿北偏西30°方向航行,乙船沿南偏西70°方向航行,已知两船的航行速度相同,如果1小时后甲、乙两船分别到达点A、B处,那么点B位于点A的( )
A.南偏西40° B.南偏西30° C.南偏西20° D.南偏西10°
19.(2022·广西玉林·二模)已知∠α=35°,那么∠α的余角等于( )
A.35° B.55° C.65° D.145°
20.(2021·广西百色·二模)等于( )
A. B. C. D.
21.(2021·广西百色·一模)下列几何体中,不管从哪个方向看到的都是圆( )
A. B.
C. D.
22.(2021·广西玉林·模拟预测)已知:∠,则∠的余角是( )
A.39° B.49° C.59° D.139°
23.(2021·广西百色·一模)下列平面图形中,经过折叠不能围成正方体的是( )
A. B. C. D.
24.(2021·广西柳州·三模)如图,OA⊥OB,若∠1=40°,则∠2的度数是
A.20° B.40° C.50° D.60°
二、填空题
25.(2022·广西·中考真题)如图摆放一副三角板,直角顶点重合,直角边所在直线分别重合,那么∠BAC的大小为______
26.(2022·广西桂林·中考真题)如图,点C是线段AB的中点,若AC=2cm,则AB=_____cm.
27.(2022·广西玉林·中考真题)已知∠α=60°,则∠α的余角等于____度.
28.(2022·广西·柳城县教育局教研室一模)如图,点D是线段AB的中点,C是线段AD的中点,若AB=8cm,则CD=___cm.
29.(2022·广西百色·一模)一个几何体由若干个大小相同的小立方块搭成,从左面和上面看到的平面图形如图所示,则搭成这个几何体的小立方块的个数为_____.
30.(2021·广西·柳城县教育局教研室一模)如图所示,建筑工人砌墙时,经常在两个墙角的位置分别插一根小桩,然后拉一条直的参照线,可以这样做的数学道理_____________.
参考答案:
1.B
【解析】根据两点之间线段最短进行解答即可.
解:∵两点之间线段最短,
∴从学校A到书店B有①、②、③、④四条路线中,最短的路线是②,故B正确.
故选:B.
本题主要考查了两点之间线段最短,解题的关键是熟练掌握两点之间所有连线中,线段最短.
2.B
【解析】根据面动成体:一个长方形绕着它的一条边所在的直线旋转一周后所得到的立体图形是圆柱,据此判断即可.
解:由题意可知:
一个长方形绕着它的一条边所在的直线旋转一周后所得到的立体图形是圆柱.
故选:B
本题考查了圆柱的概念和面动成体,属于应知应会题型,熟练掌握基础知识是解题关键.
3.B
【解析】根据互为余角相加等于以及度分秒的进率计算即可.
解:∵∠α=25°30′,
∴它的余角为,
故选:B.
本题主要考查余角的性质以及度分秒的计算,熟知度分秒的进率为60是解题的关键.
4.D
【解析】根据正方体的展开图特征解题.
解:A.是正方体的展开图,故A不符合题意;
B.是正方体的展开图,故B不符合题意;
C.是正方体的展开图,故C不符合题意;
D.不是正方体的展开图,故D符合题意,
故选:D.
本题考查正方体的展开图,熟知正方体的11种展开图是解题关键.
5.A
【解析】根据三视图的法则可得出答案.
解:左视图为从左往右看得到的视图,
A.球的左视图是圆,
B.圆柱的左视图是长方形,
C.圆锥的左视图是等腰三角形,
D.圆台的左视图是等腰梯形,
故符合题意的选项是A.
错因分析 较容易题.失分原因是不会判断常见几何体的三视图.
6.D
【解析】根据各个图形的侧面展开图求得正确答案,即可.
解:A选项,正方体的侧面展开图不是扇形,不符合题意;
B选项,长方体的侧面展开图不是扇形,不符合题意;
C选项,圆柱的侧面展开图是长方形或正方形,不是扇形,不符合题意;
D选项,圆锥的侧面展开图是扇形,符合题意.
故选:D.
本题考查了几何体的侧面展开图,熟悉选项中每个图形的侧面展开图是解题的关键.
7.C
【解析】根据两角和为90度,这两角互为余角求解即可.
解:∠α的余角=90°-∠α=90°-20°=70°,
故选:C.
本题考查余角的概念,熟练掌握余角的概念是解题的关键.
8.B
【解析】由图可知展开侧面为扇形,则该几何体为圆锥.
解:该几何体的侧面展开图是扇形,所以这个几何体可能是圆锥,
故选:B.
此题主要考查几何体的展开图,熟记几何体的侧面展开图是解题的关键.
9.C
【解析】分两种情况讨论,即①当 在 内部时,②当在外部时,先根据题意画图,然后根据角的和差关系计算即可.
解:①如图,当在内部时,
;
②如图,当在外部时,
;
综上所述,的度数为和.
故选:C.
本题考查了几何图形中角的计算,解题的关键是注意分两种情况讨论.
10.B
【解析】根据三棱锥的四个面都是三角形,还要能围成一个立体图形,进而分析得出即可.
解:A.此图形可以围成三棱柱,故此选项不符合题意;
B.此图形可以围成三棱锥,故此选项符合题意;
C.此图形可以围成四棱锥,故此选项不符合题意;
D.无法围成立体图形,故此选项不符合题意.
故选:B.
本题主要考查了几何体的展开图,注意几何体的形状特点进而分析才行.
11.D
【解析】根据侧面展开图为一个扇形,底面是一个圆,所以该几何体是圆锥.
解:由题意,
∵侧面展开图为一个扇形,底面是一个圆,
∴该几何体是圆锥体;
故选:D
本题考查了几何体的侧面展开图,从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
12.B
【解析】根据圆锥的侧面展开图为扇形判断即可.
解:由圆锥的侧面展开图是扇形可知选B,
故选:B.
本题主要考查圆锥侧面展开图的形状,题型比较简单,熟知关于圆锥的知识点是解决本题的关键.
13.A
【解析】根据直线的特征,经过两点有一直线并且只有一条直线即可判断.
解:设线段m与挡板的交点为A,a、b、c、d与挡板的交点分别为B,C,D,E,
连结AB、AC、AD、AE,
根据直线的特征经过两点有且只有一条直线,
利用直尺可确定线段a与m在同一直线上,
故选择A.
本题考查直线的特征,掌握直线的特征是解题关键.
14.B
【解析】根据角平分线的定义判断即可.
解:A选项.∵∠AOC=∠BOC
∴OC平分∠AOB.
所以A选项正确,不符合题意;
B选项.∵∠AOC+∠COB=∠AOB,
∴OC不一定平分∠AOB.
所以B选项不正确,符合题意;
C选项.∵∠AOB=2∠BOC,
∴OC平分∠AOB.
所以C选项正确,不符合题意;
D.∵,
∴OC平分∠AOB.
所以D选项正确,不符合题意.
故选:B.
本题考查了角平分线的定义,解决本题的关键是掌握角平分线的定义.
15.A
【解析】根据一个几何体有几个面,则截面最多是几边形,由于棱柱没有曲面,所以用一个平面去截棱柱,截面不可能是圆.
A选项:截面不可能是圆,故正确;;
B选项:截面可能是圆,故错误;
C选项:截面可能是圆,故错误;
D选项:截面一定是圆,故错误.
故选A.
本题考查截面的定义,同时应注意的是截面的形状随截法的不同而改变,若一个几何体有几个面,则截面最多是几边形.
16.D
【解析】根据正方体平面展开图的特征得出每个相对面,再由相对面上的两个数互为相反数可得出x的值.
解:“3”与“-3”相对,“y”与“-2”相对,“x”与“-8”相对, 故x=8,故选D.
本题主要考查了正方体相对面上的文字,解决本题的关键是要熟练掌握正方体展开图的特征.
17.B
【解析】根据小单位化大单位除以进率,可得答案.
解: ∠P=25°12′=25.2°,∠R=25.2°
所以B选项是正确的.
本题考查角的大小比较.关键是将单位统一,即度、分、秒的换算.
18.C
试题分析:由甲船沿北偏西30°方向航行,乙船沿南偏西70°方向航行,得出∠BOA的度数,由两船的航行速度相同,得出AO=BO,得出∠BAO=50°,以及求出∠BAD的度数,得出点B位于点A的方向,故本题选C.
点睛:本题主要考查的就是方位角的问题,属于中等难度题型.解决这个问题的关键就是要能够根据已知的条件得出各个角的度数,从而求出问题中所要求的角的度数.在解决这种类型的题目时,我们还要注意参照物是那个物体,就要以参照物为标注建立方位图,从而得出答案.
19.B
【解析】根据余角的定义:如果两个角的和等于90°(直角),就说这两个角互为余角计算.
解:∵∠α=35°,
∴它的余角等于90°﹣35°=55°.
故选B.
本题考查余角的概念,掌握概念正确计算是本题的解题关键.
20.C
【解析】根据度分秒之间的进制关系,进行计算即可.
解:;
故选C.
本题考查度分秒的计算.熟练掌握度分秒之间的进制关系,是解题的关键.
21.B
【解析】球体不管从哪个方向看到的都是圆,据此判断即可.
解:不管从哪个方向看到的都是圆的是球体,
故选:B.
本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.
22.B
【解析】直接根据余角的概念解答即可.
:根据余角的概念,这个角的余角为:90°-41°=49°.
故选:B.
本题考查了余角的概念:如果两个角的和等于90°,就说这两个角互为余角.
23.C
【解析】根据正方体展开图的常见形式作答即可.
解:由展开图可知:、、能围成正方体,故不符合题意;
、围成几何体时,有两个面重合,不能围成正方体,故符合题意.
故选:.
本题主要考查展开图折叠成几何体的知识点,注意只要有“田、凹”字格的展开图都不是正方体的表面展开图.
24.C
∵OA⊥OB,∴∠AOB=90°.
又∵∠1=40°,∴∠2=∠AOB-∠1=90°-40°=50°,
故选C.
25.135°##135度
【解析】根据三角板及其摆放位置可得,求解即可.
,
,
故答案为:135°.
本题考查了求一个角的补角,即两个角的和为180度时,这两个角互为补角,熟练掌握知识点是解题的关键.
26.4
【解析】根据中点的定义可得AB=2AC=4cm.
解:根据中点的定义可得:AB=2AC=2×2=4(cm),
故答案为:4.
本题主要考查中点的定义,熟知中点的定义是解题关键.
27.30
∵互余两角的和等于90°,
∴α的余角为:90°-60°=30°.
故答案为:30
28.2
【解析】由点D是线段AB的中点,C是线段AD的中点,可得,即可求得答案.
解:∵点D是线段AB的中点,
∴,
∵C是线段AD的中点,
∴,
∴,
故答案为:2.
本题主要考查线段的中点,熟练运用线段的中点求线段长是解题的关键.
29.4
【解析】根据左面看与上面看的图形,得到俯视图解答即可.
解:根据左视图和俯视图,这个几何体的底层有3个小正方体,
第二层有1个小正方体,
所以有个小正方体,
故答案为:4.
本题主要考查从不同方向看几何体,熟练掌握几何体的特征是解题的关键.
30.两点确定一条直线
【解析】根据两点确定一条直线判断即可;
经常在两个墙角的位置分别插一根小桩,然后拉一条直的参照线,可以这样做的数学道理两点确定一条直线;
故答案是两点确定一条直线.
本题主要考查了点与线的关系,准确判断是解题的关键.
