【新课标】6.4.2数据的离散程度 课件(共25张PPT)
文档属性
| 名称 | 【新课标】6.4.2数据的离散程度 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-12 11:22:10 | ||
图片预览







文档简介
(共25张PPT)
6.4.2数据的离散程度
北师大版八年级上册
教学目标
1.通过更为丰富的例子,让学生较为全面地理解方差及其在现实生活中的应用。
2.通过实例,让学生体会数据的离散程度在现实生活中广泛存在,应视情况分析方差或标准差对于问题的影响。
情境导入
1.刻画一组数据的离散程度有哪些统计量?
2.如何求极差、方差和标准差?
极差=最大数据-最小数据;
方差:
极差
方差
标准差
标准差:是方差的算术平方根.
新知讲解
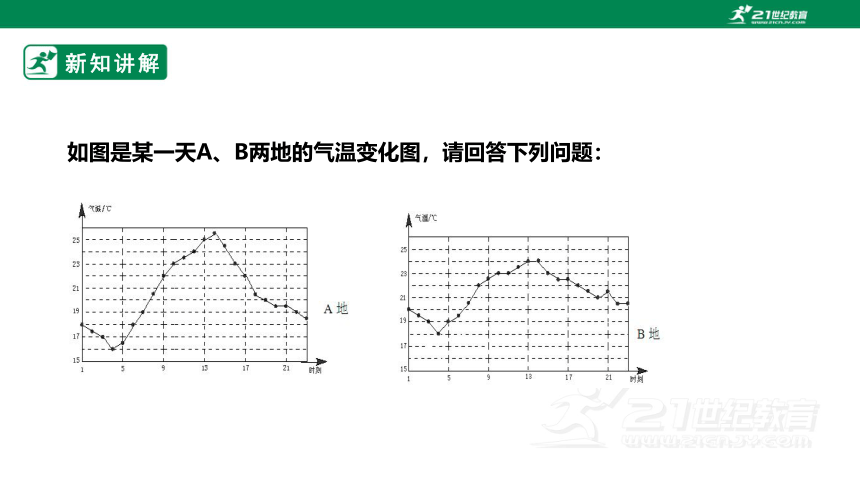
如图是某一天A、B两地的气温变化图,请回答下列问题:
新知讲解
(1)不进行计算,说说A、B两地这一天气温的特点.
(2)分别计算这一天A、B两地气温的平均数和方差,与你刚才的看法一致吗?
A、B两地平均气温相近,但A地日温差较大,B地日温差较小.
A地平均气温20.42 ℃,方差7.76;
B地平均气温21.35 ℃,方差2.78.
议一议
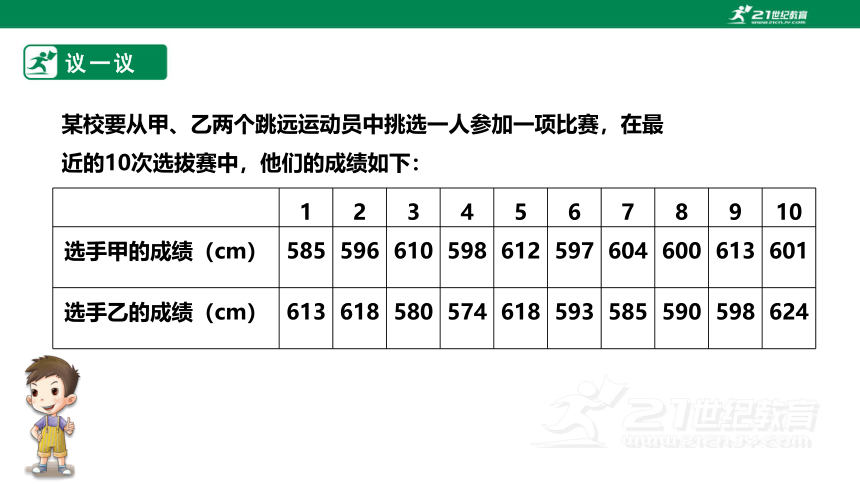
某校要从甲、乙两个跳远运动员中挑选一人参加一项比赛,在最近的10次选拔赛中,他们的成绩如下:
1 2 3 4 5 6 7 8 9 10
选手甲的成绩(cm) 585 596 610 598 612 597 604 600 613 601
选手乙的成绩(cm) 613 618 580 574 618 593 585 590 598 624
新知讲解
(4)历届比赛表明,成绩达到5.96cm就很可能夺冠,你认为为了夺冠应选谁参加这项比赛?
(5)如果历届比赛表明,成绩达到6.10cm就能打破记录,你认为为了打破记录应选谁参加这项比赛?
(1) 他们的平均成绩分别是多少?
(2) 甲、乙这10次比赛成绩的方差分别是多少?
(3)这两名运动员的运动成绩各有什么特点?
新知讲解
解:(1)甲的平均成绩是:601.6cm,乙的平均成绩是:599.3cm;
(2)甲的方差是:65.84,乙的方差是:284.21;
(3)甲运动员成绩较稳定,因为极差、方差都比较小,
甲的平均成绩比乙好
乙较有潜质,因为乙的最远成绩比甲的最远成绩好
(4)从平均数分析可知,甲、乙两队员都有夺冠的可能.但由方差分析可知,甲成绩比较平稳,夺冠的可能性比乙大.
(5)要打破纪录,成绩要比较突出,因此乙队员打破纪录的可能性大,我认为为了打破纪录,应选乙队员参加这项比赛.
归纳总结
(1)在解决实际问题时,方差的作用是什么?
反映数据的波动大小.方差越大,数据的波动越大;方差越小,数据的波动越小,可用样本方差估计总体方差.
(2)运用方差解决实际问题的一般步骤是怎样的?
先计算样本数据平均数,当两组数据的平均数相等或相近时,再利用样本方差来估计总体数据的波动情况.实际问题中,可能越稳定越好,也可能越不稳定越好。有时方差的大小只能说明一种波动大小,不能说明优势劣势。
做一做
(1)两人一组,在安静的环境中,一人估计1分钟的时间,另一人记下实际时间,将结果记录下来。
(2)在吵闹的环境中,再做一次这样的试验。
(3)将全班的结果汇总起来,并分别计算安静状态和吵闹环境中估计结果的平均值和方差。
(4)两种情况下的结果是否一致?说明理由。
典例精析
例、为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图(其中男生收看3次的人数没有标出).
根据上述信息,解答下列问题:
(1)该班级女生人数是______,
女生收看“两会”新闻次
数的中位数是_______次.
20
3
典例精析
(2)对于某个群体,我们把一周内收看某热点新闻次数不低于3次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低5%,试求该班级男生人数.
由题意知,该班级女生对“两会”新闻的“关注指数”为×100%=65%,所以男生对“两会”新闻的“关注指数”为60%.
设该班级的男生有x人,则=60%,
解得x=25. 所以该班级男生有25人.
典例精析
(3)为进一步分析该班级男、女生收看“两会”新闻次数的特点,小明给出了男生的部分统计量(如表).
统计量 平均数/次 中位数/次 众数/次 方差
该班级男生 3 3 4 2
根据你所学过的统计知识,适当计算女生的有关统计量,进而比较该班级男、女生收看“两会”新闻次数的波动大小.
典例精析
该班级女生收看“两会”新闻次数的平均数为
=3(次),
女生收看“两会”新闻次数的方差为
[2×(1-3)2+5×(2-3)2+6×(3-3)2+5×(4-3)2+2×(5-3)2]=.
因为2>,所以男生比女生的波动大.
课堂练习
1.下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙
C.丙 D.丁
甲 乙 丙 丁
平均数/cm 185 180 185 180
方差 3.6 3.6 7.4 8.1
A
课堂练习
2.甲、乙、丙、丁四名射击运动员在选拔赛中,每人射击了10次,甲、乙两人的成绩如表所示.丙、丁两人的成绩如图所示.欲选一名运动员参赛,从平均数与方差两个因素分析,应选( )
甲 乙
平均数 9 8
方差 1 1
A. 甲 B.乙 C.丙 D.丁
C
课堂练习
3.要从甲、乙两名同学中选出一名同学代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.
(1)已求得甲的平均成绩为8环,求乙的平均成绩;
解:(1)乙的平均成绩是
(8+9+8+8+7+8+9+8+8+7)÷10=8(环).
(2)观察图形,直接写出甲、乙这10次射击成绩的方差, , 哪个大;
(3)如果其他班级参赛选手的射击成绩都在7环左右,那么本班应该选_____参赛更合适;如果其他班级参赛选手的射击成绩都在9环左右,那么本班应该选 参赛更合适.
乙
甲
课堂练习
4.某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间每人踢100个以上(含100个)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛成绩(单位:个):
1号 2号 3号 4号 5号 总分
甲班 100 98 110 89 103 500
乙班 89 100 95 119 97 500
课堂练习
经统计发现两班总分相等,此时有学生建议,可以通过考查数据中的其他信息作为参考.
请你回答下列问题:
(1)计算甲、乙两班的优秀率.
(2)求两班比赛成绩的中位数.
(3)估计两班比赛成绩的方差哪一个较小.
(4)根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述理由.
课堂练习
解:(1)甲班的优秀率为×100%=60%;
乙班的优秀率为×100%=40%.
(2)甲、乙两班比赛成绩的中位数分别是100个和97个.
(3)甲班的方差较小.
(4)甲班.因为甲班5人比赛成绩的优秀率比乙班高,中位数比乙班大,方差比乙班小,综合评定甲班成绩较好.
课堂总结
根据方差做决策
方差的作用:比较数据的稳定性
利用方差解答实际问题
板书设计
数据的离散程度
1、方差的作用
2、利用方差解答实际问题
作业布置
教材153页习题第2,3,4题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
6.4.2数据的离散程度
北师大版八年级上册
教学目标
1.通过更为丰富的例子,让学生较为全面地理解方差及其在现实生活中的应用。
2.通过实例,让学生体会数据的离散程度在现实生活中广泛存在,应视情况分析方差或标准差对于问题的影响。
情境导入
1.刻画一组数据的离散程度有哪些统计量?
2.如何求极差、方差和标准差?
极差=最大数据-最小数据;
方差:
极差
方差
标准差
标准差:是方差的算术平方根.
新知讲解
如图是某一天A、B两地的气温变化图,请回答下列问题:
新知讲解
(1)不进行计算,说说A、B两地这一天气温的特点.
(2)分别计算这一天A、B两地气温的平均数和方差,与你刚才的看法一致吗?
A、B两地平均气温相近,但A地日温差较大,B地日温差较小.
A地平均气温20.42 ℃,方差7.76;
B地平均气温21.35 ℃,方差2.78.
议一议
某校要从甲、乙两个跳远运动员中挑选一人参加一项比赛,在最近的10次选拔赛中,他们的成绩如下:
1 2 3 4 5 6 7 8 9 10
选手甲的成绩(cm) 585 596 610 598 612 597 604 600 613 601
选手乙的成绩(cm) 613 618 580 574 618 593 585 590 598 624
新知讲解
(4)历届比赛表明,成绩达到5.96cm就很可能夺冠,你认为为了夺冠应选谁参加这项比赛?
(5)如果历届比赛表明,成绩达到6.10cm就能打破记录,你认为为了打破记录应选谁参加这项比赛?
(1) 他们的平均成绩分别是多少?
(2) 甲、乙这10次比赛成绩的方差分别是多少?
(3)这两名运动员的运动成绩各有什么特点?
新知讲解
解:(1)甲的平均成绩是:601.6cm,乙的平均成绩是:599.3cm;
(2)甲的方差是:65.84,乙的方差是:284.21;
(3)甲运动员成绩较稳定,因为极差、方差都比较小,
甲的平均成绩比乙好
乙较有潜质,因为乙的最远成绩比甲的最远成绩好
(4)从平均数分析可知,甲、乙两队员都有夺冠的可能.但由方差分析可知,甲成绩比较平稳,夺冠的可能性比乙大.
(5)要打破纪录,成绩要比较突出,因此乙队员打破纪录的可能性大,我认为为了打破纪录,应选乙队员参加这项比赛.
归纳总结
(1)在解决实际问题时,方差的作用是什么?
反映数据的波动大小.方差越大,数据的波动越大;方差越小,数据的波动越小,可用样本方差估计总体方差.
(2)运用方差解决实际问题的一般步骤是怎样的?
先计算样本数据平均数,当两组数据的平均数相等或相近时,再利用样本方差来估计总体数据的波动情况.实际问题中,可能越稳定越好,也可能越不稳定越好。有时方差的大小只能说明一种波动大小,不能说明优势劣势。
做一做
(1)两人一组,在安静的环境中,一人估计1分钟的时间,另一人记下实际时间,将结果记录下来。
(2)在吵闹的环境中,再做一次这样的试验。
(3)将全班的结果汇总起来,并分别计算安静状态和吵闹环境中估计结果的平均值和方差。
(4)两种情况下的结果是否一致?说明理由。
典例精析
例、为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图(其中男生收看3次的人数没有标出).
根据上述信息,解答下列问题:
(1)该班级女生人数是______,
女生收看“两会”新闻次
数的中位数是_______次.
20
3
典例精析
(2)对于某个群体,我们把一周内收看某热点新闻次数不低于3次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低5%,试求该班级男生人数.
由题意知,该班级女生对“两会”新闻的“关注指数”为×100%=65%,所以男生对“两会”新闻的“关注指数”为60%.
设该班级的男生有x人,则=60%,
解得x=25. 所以该班级男生有25人.
典例精析
(3)为进一步分析该班级男、女生收看“两会”新闻次数的特点,小明给出了男生的部分统计量(如表).
统计量 平均数/次 中位数/次 众数/次 方差
该班级男生 3 3 4 2
根据你所学过的统计知识,适当计算女生的有关统计量,进而比较该班级男、女生收看“两会”新闻次数的波动大小.
典例精析
该班级女生收看“两会”新闻次数的平均数为
=3(次),
女生收看“两会”新闻次数的方差为
[2×(1-3)2+5×(2-3)2+6×(3-3)2+5×(4-3)2+2×(5-3)2]=.
因为2>,所以男生比女生的波动大.
课堂练习
1.下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙
C.丙 D.丁
甲 乙 丙 丁
平均数/cm 185 180 185 180
方差 3.6 3.6 7.4 8.1
A
课堂练习
2.甲、乙、丙、丁四名射击运动员在选拔赛中,每人射击了10次,甲、乙两人的成绩如表所示.丙、丁两人的成绩如图所示.欲选一名运动员参赛,从平均数与方差两个因素分析,应选( )
甲 乙
平均数 9 8
方差 1 1
A. 甲 B.乙 C.丙 D.丁
C
课堂练习
3.要从甲、乙两名同学中选出一名同学代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.
(1)已求得甲的平均成绩为8环,求乙的平均成绩;
解:(1)乙的平均成绩是
(8+9+8+8+7+8+9+8+8+7)÷10=8(环).
(2)观察图形,直接写出甲、乙这10次射击成绩的方差, , 哪个大;
(3)如果其他班级参赛选手的射击成绩都在7环左右,那么本班应该选_____参赛更合适;如果其他班级参赛选手的射击成绩都在9环左右,那么本班应该选 参赛更合适.
乙
甲
课堂练习
4.某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间每人踢100个以上(含100个)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛成绩(单位:个):
1号 2号 3号 4号 5号 总分
甲班 100 98 110 89 103 500
乙班 89 100 95 119 97 500
课堂练习
经统计发现两班总分相等,此时有学生建议,可以通过考查数据中的其他信息作为参考.
请你回答下列问题:
(1)计算甲、乙两班的优秀率.
(2)求两班比赛成绩的中位数.
(3)估计两班比赛成绩的方差哪一个较小.
(4)根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述理由.
课堂练习
解:(1)甲班的优秀率为×100%=60%;
乙班的优秀率为×100%=40%.
(2)甲、乙两班比赛成绩的中位数分别是100个和97个.
(3)甲班的方差较小.
(4)甲班.因为甲班5人比赛成绩的优秀率比乙班高,中位数比乙班大,方差比乙班小,综合评定甲班成绩较好.
课堂总结
根据方差做决策
方差的作用:比较数据的稳定性
利用方差解答实际问题
板书设计
数据的离散程度
1、方差的作用
2、利用方差解答实际问题
作业布置
教材153页习题第2,3,4题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
