26.1.2 反比例函数图像和性质 课件 (共27张PPT)
文档属性
| 名称 | 26.1.2 反比例函数图像和性质 课件 (共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-12 22:05:56 | ||
图片预览





文档简介
(共27张PPT)
第二十六章 反比例函数
26.1 反比例函数
26.1.2 反比例函数的图 像和性质
主讲人:数学可以很简单
1. 经历画反比例函数的图象、归纳得到反比例函数的图象特征和性质的过程 (重点、难点)
2. 会画反比例函数图象,了解和掌握反比例函数的图象和性质. (重点)
3. 能够初步应用反比例函数的图象和性质解题. (重点、难点)
一次函数的图像
二次函数的图像
y = kx + b(k ≠ 0)
一条直线
y = ax2 + bx + c(a ≠ 0)
一条抛物线
例1 画反比例函数与的图象.
知识点1 反比例函数的图像
分析:可以采用“描点”的方法画函数图像.
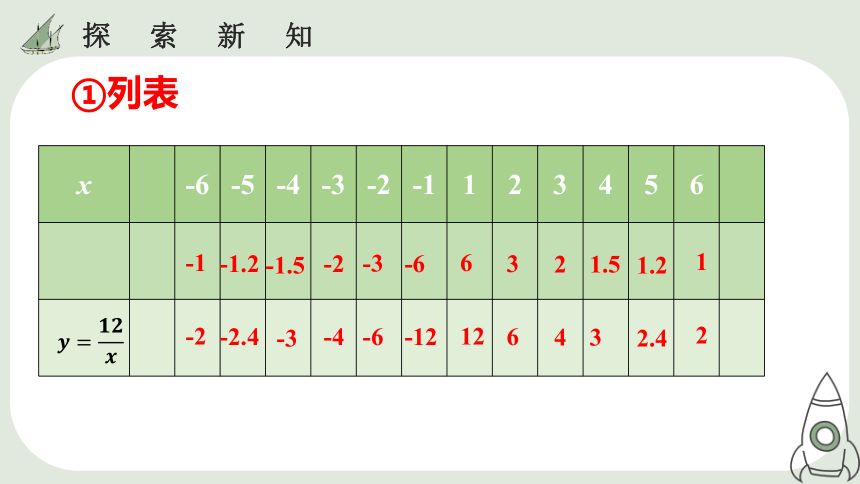
①列表
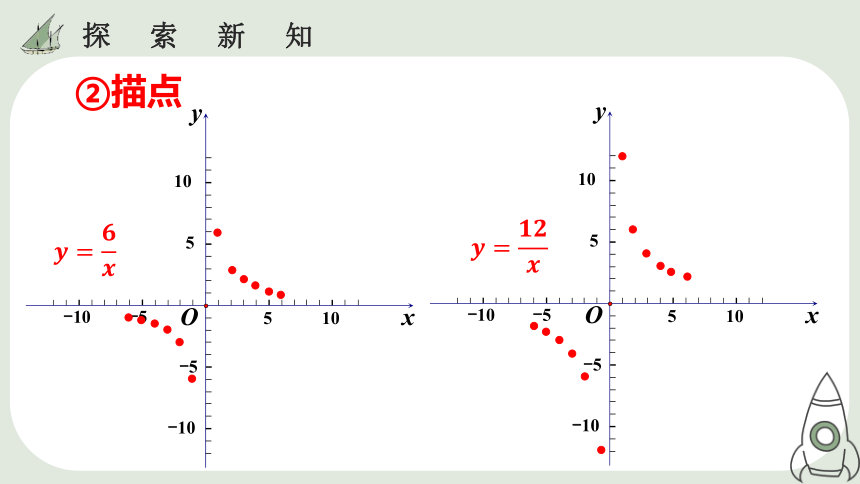
②描点
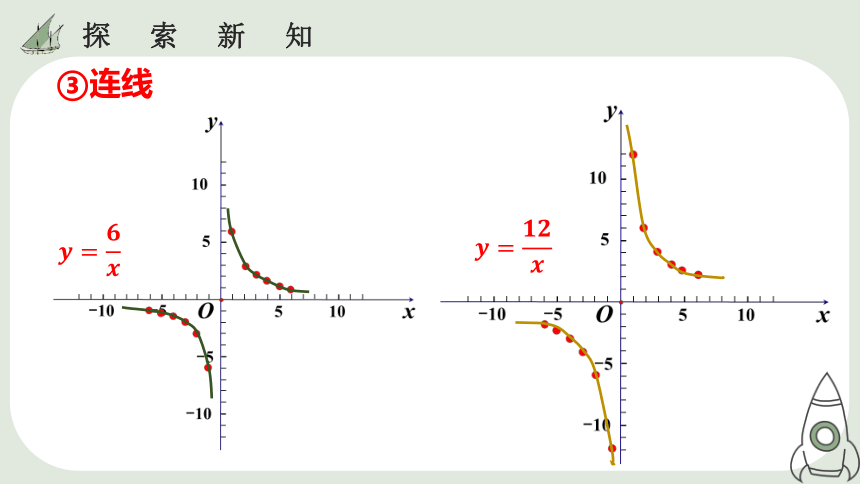
③连线
自变量x不能为0
x -6 -5 -4 -3 -2 -1 1 2 3 4 5 6
①列表
-1
-1.2
-1.5
-2
-3
-6
6
3
2
1.5
1.2
1
-2
-2.4
-3
-4
-6
-12
12
6
4
3
2.4
2
②描点
5
10
x
5
10
-5
-10
-5
-10
y
O
5
10
x
5
10
-5
-10
-5
-10
y
O
③连线
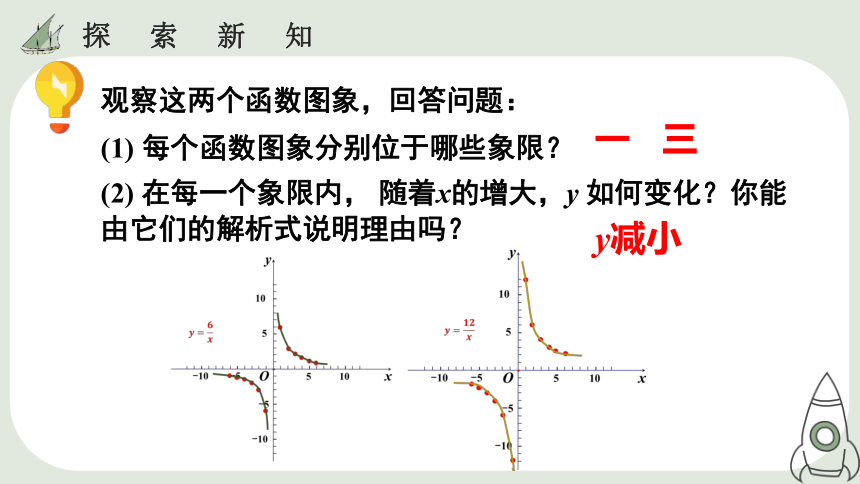
观察这两个函数图象,回答问题:
(1) 每个函数图象分别位于哪些象限?
(2) 在每一个象限内, 随着x的增大,y 如何变化?你能由它们的解析式说明理由吗?
一 三
y减小
(3) 对于反比例函数(k>0),考虑问题(1)(2),你能得出同样的结论吗?
x
y
反比例函数的图像和性质:
由两条曲线组成,且分别位于第一、三象限,它们与 x 轴、y 轴都不相交;
在每个象限内,y 随 x 的增大而减小.
k<0
回顾上面我们利用函数图象,从特殊到一般研究反比例函数(k>0) 的性质的过程,你能用类似的方法研究反比例函数(k<0)的图象和性质吗?
y
x
O
反比例函数的图像和性质:
由两条曲线组成,且分别位于第二、四象限
它们与x轴、y轴都不相交;
在每个象限内,y随x的增大而增大.
k>0
归纳:
一般地,反比例函数的图象是双曲线,它具有以下性质:
(1) 当 k > 0 时,双曲线的两支分别位于第一、三象限,在每一象限内,y 随 x 的增大而减小;
(2) 当 k < 0 时,双曲线的两支分别位于第二、四象限,在每一象限内,y 随 x 的增大而增大.
例1 已知反比例函数的图象经过点 A (2,6).
(1) 这个函数的图象位于哪些象限?y 随 x 的增大如何变化?
(2) 点B(3,4),C( , ),D(2,5)是否在这个 函数的图象上?
知识点2 待定系数法求反比例函数的解析式
解:因为点 A (2,6) 在第一象限,
所以这个函数的图象位于第一、三象限;
在每一个象限内,y 随 x 的增大而减小.
解:设这个反比例函数的解析式为y=,因为点 A (2,6)在其图象上,所以有6=,解得 k =12.
所以反比例函数的解析式为y= .
因为点 B,C 的坐标都满足该解析式,而点 D的坐标不满足,所以点 B,C 在这个函数的图象上,点 D 不在这个函数的图象上.
(2) 点B(3,4),C( , ),D(2,5)是否在这个 函数的图象上?
例2 如图,是反比例函数图象的一支. 根据图象,回答下列问题:
(1) 图象的另一支位于哪个象限?常数 m 的取值范围是什么?
(2) 在这个函数图象的某一支上任取点 A (x1,y1) 和点B (x2,y2). 如果x1>x2,那么 y1 和 y2 有怎样的大小关系?
知识点3 反比例函数图像和性质的综合
O
x
y
解:因为这个反比例函数图象的一支位于第一象限,所以另一支必位于第三象限.
因为这个函数图象位于第一、三象限,所以m-5>0,解得m>5.
(2) 在这个函数图象的某一支上任取点 A (x1,y1) 和点B (x2,y2). 如果x1>x2,那么 y1 和 y2 有怎样的大小关系?
解:因为 m-5 > 0,
所以在这个函数图象的任一支上,y 都随 x 的增大而减小,
因此当x1>x2时,
y1<y2.
练习1 下列图象中是反比例函数图象的是( ).
C
A B C D
练习2 如图所示的图象对应的函数解析为( ).
A. y = 5x
B. y = 2x + 3
C.
D.
C
练习3 填空:
(1)反比例函数的图象在第______象限.
(2)反比例函数的图象如图所示,则k___0;在图象的每一支上,y随x的增大而_____.
一、三
<
增大
练习4 下列关于反比例函数的图象的三个结论:
(1) 经过点 (-1,12) 和点 (10,-1.2);
(2) 在每一个象限内,y 随 x 的增大而减小;
(3) 双曲线位于二、四象限.
其中正确的是 (填序号).
(1)(3)
练习5 点 (a-1,y1),(a+1,y2)在反比例函数 (k>0)的图象上,若y1<y2,求a的取值范围.
解:由题意知,在图象的每一支上,y 随 x 的增大而减小.
① 当这两点在图象的同一支上时,
∵y1<y2,∴a-1>a+1, 无解;
②当这两点分别位于图象的两支上时,
∵y1<y2,∴必有 y1<0<y2.
∴a-1<0,a+1>0, 解得:-1<a<1.
故 a 的取值范围为:-1<a<1.
练习6.已知一个反比例函数的图象经过点 A(3, – 4).
(1)这个函数的图象位于哪些象限?在图象的每一支上,y 随 x 的增大如何变化?
(2)点 B( – 3,4),C( – 2,6),D(3,4)是否在这个函数的图象上?为什么?
第二、第四象限
增大
点 B、C 在这个函数图象上,点 D 不在这个函数的图象上.
练习7 已知点A(x1,y1),B(x2,y2)在反比例函数的图象上.如果 x1<x2,而且 x1,x2 同号,那么 y1,y2 有怎样的大小关系?为什么?
解:因为函数的图象位于第一、第三象限,
所以在每个象限内,y 随 x 的增大而减小.
因为 x1<x2,所以 y1>y2.
反比例函数的图像:
反比例函数的性质:
(1) 当 k > 0 时,双曲线的两支分别位于第一、三象限,在每一象限内,y 随 x 的增大而减小;
(2) 当 k < 0 时,双曲线的两支分别位于第二、四象限,在每一象限内,y 随 x 的增大而增大.
k < 0
k > 0
第二十六章 反比例函数
26.1 反比例函数
26.1.2 反比例函数的图 像和性质
主讲人:数学可以很简单
1. 经历画反比例函数的图象、归纳得到反比例函数的图象特征和性质的过程 (重点、难点)
2. 会画反比例函数图象,了解和掌握反比例函数的图象和性质. (重点)
3. 能够初步应用反比例函数的图象和性质解题. (重点、难点)
一次函数的图像
二次函数的图像
y = kx + b(k ≠ 0)
一条直线
y = ax2 + bx + c(a ≠ 0)
一条抛物线
例1 画反比例函数与的图象.
知识点1 反比例函数的图像
分析:可以采用“描点”的方法画函数图像.
①列表
②描点
③连线
自变量x不能为0
x -6 -5 -4 -3 -2 -1 1 2 3 4 5 6
①列表
-1
-1.2
-1.5
-2
-3
-6
6
3
2
1.5
1.2
1
-2
-2.4
-3
-4
-6
-12
12
6
4
3
2.4
2
②描点
5
10
x
5
10
-5
-10
-5
-10
y
O
5
10
x
5
10
-5
-10
-5
-10
y
O
③连线
观察这两个函数图象,回答问题:
(1) 每个函数图象分别位于哪些象限?
(2) 在每一个象限内, 随着x的增大,y 如何变化?你能由它们的解析式说明理由吗?
一 三
y减小
(3) 对于反比例函数(k>0),考虑问题(1)(2),你能得出同样的结论吗?
x
y
反比例函数的图像和性质:
由两条曲线组成,且分别位于第一、三象限,它们与 x 轴、y 轴都不相交;
在每个象限内,y 随 x 的增大而减小.
k<0
回顾上面我们利用函数图象,从特殊到一般研究反比例函数(k>0) 的性质的过程,你能用类似的方法研究反比例函数(k<0)的图象和性质吗?
y
x
O
反比例函数的图像和性质:
由两条曲线组成,且分别位于第二、四象限
它们与x轴、y轴都不相交;
在每个象限内,y随x的增大而增大.
k>0
归纳:
一般地,反比例函数的图象是双曲线,它具有以下性质:
(1) 当 k > 0 时,双曲线的两支分别位于第一、三象限,在每一象限内,y 随 x 的增大而减小;
(2) 当 k < 0 时,双曲线的两支分别位于第二、四象限,在每一象限内,y 随 x 的增大而增大.
例1 已知反比例函数的图象经过点 A (2,6).
(1) 这个函数的图象位于哪些象限?y 随 x 的增大如何变化?
(2) 点B(3,4),C( , ),D(2,5)是否在这个 函数的图象上?
知识点2 待定系数法求反比例函数的解析式
解:因为点 A (2,6) 在第一象限,
所以这个函数的图象位于第一、三象限;
在每一个象限内,y 随 x 的增大而减小.
解:设这个反比例函数的解析式为y=,因为点 A (2,6)在其图象上,所以有6=,解得 k =12.
所以反比例函数的解析式为y= .
因为点 B,C 的坐标都满足该解析式,而点 D的坐标不满足,所以点 B,C 在这个函数的图象上,点 D 不在这个函数的图象上.
(2) 点B(3,4),C( , ),D(2,5)是否在这个 函数的图象上?
例2 如图,是反比例函数图象的一支. 根据图象,回答下列问题:
(1) 图象的另一支位于哪个象限?常数 m 的取值范围是什么?
(2) 在这个函数图象的某一支上任取点 A (x1,y1) 和点B (x2,y2). 如果x1>x2,那么 y1 和 y2 有怎样的大小关系?
知识点3 反比例函数图像和性质的综合
O
x
y
解:因为这个反比例函数图象的一支位于第一象限,所以另一支必位于第三象限.
因为这个函数图象位于第一、三象限,所以m-5>0,解得m>5.
(2) 在这个函数图象的某一支上任取点 A (x1,y1) 和点B (x2,y2). 如果x1>x2,那么 y1 和 y2 有怎样的大小关系?
解:因为 m-5 > 0,
所以在这个函数图象的任一支上,y 都随 x 的增大而减小,
因此当x1>x2时,
y1<y2.
练习1 下列图象中是反比例函数图象的是( ).
C
A B C D
练习2 如图所示的图象对应的函数解析为( ).
A. y = 5x
B. y = 2x + 3
C.
D.
C
练习3 填空:
(1)反比例函数的图象在第______象限.
(2)反比例函数的图象如图所示,则k___0;在图象的每一支上,y随x的增大而_____.
一、三
<
增大
练习4 下列关于反比例函数的图象的三个结论:
(1) 经过点 (-1,12) 和点 (10,-1.2);
(2) 在每一个象限内,y 随 x 的增大而减小;
(3) 双曲线位于二、四象限.
其中正确的是 (填序号).
(1)(3)
练习5 点 (a-1,y1),(a+1,y2)在反比例函数 (k>0)的图象上,若y1<y2,求a的取值范围.
解:由题意知,在图象的每一支上,y 随 x 的增大而减小.
① 当这两点在图象的同一支上时,
∵y1<y2,∴a-1>a+1, 无解;
②当这两点分别位于图象的两支上时,
∵y1<y2,∴必有 y1<0<y2.
∴a-1<0,a+1>0, 解得:-1<a<1.
故 a 的取值范围为:-1<a<1.
练习6.已知一个反比例函数的图象经过点 A(3, – 4).
(1)这个函数的图象位于哪些象限?在图象的每一支上,y 随 x 的增大如何变化?
(2)点 B( – 3,4),C( – 2,6),D(3,4)是否在这个函数的图象上?为什么?
第二、第四象限
增大
点 B、C 在这个函数图象上,点 D 不在这个函数的图象上.
练习7 已知点A(x1,y1),B(x2,y2)在反比例函数的图象上.如果 x1<x2,而且 x1,x2 同号,那么 y1,y2 有怎样的大小关系?为什么?
解:因为函数的图象位于第一、第三象限,
所以在每个象限内,y 随 x 的增大而减小.
因为 x1<x2,所以 y1>y2.
反比例函数的图像:
反比例函数的性质:
(1) 当 k > 0 时,双曲线的两支分别位于第一、三象限,在每一象限内,y 随 x 的增大而减小;
(2) 当 k < 0 时,双曲线的两支分别位于第二、四象限,在每一象限内,y 随 x 的增大而增大.
k < 0
k > 0
