26.2 实际问题与反比例函数 课件(共26张PPT)
文档属性
| 名称 | 26.2 实际问题与反比例函数 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-12 22:02:03 | ||
图片预览







文档简介
(共26张PPT)
第二十六章 反比例函数
26.2 实际问题与反比例函数
主讲人:数学可以很简单
能够通过分析实际问题中变量之间的关系,
建立反比例函数模型解决问题,进一步提高运用函数的图象
、性质的综合能力. (重点、难点)
2. 能够根据实际问题确定自变量的取值范围.(重点)
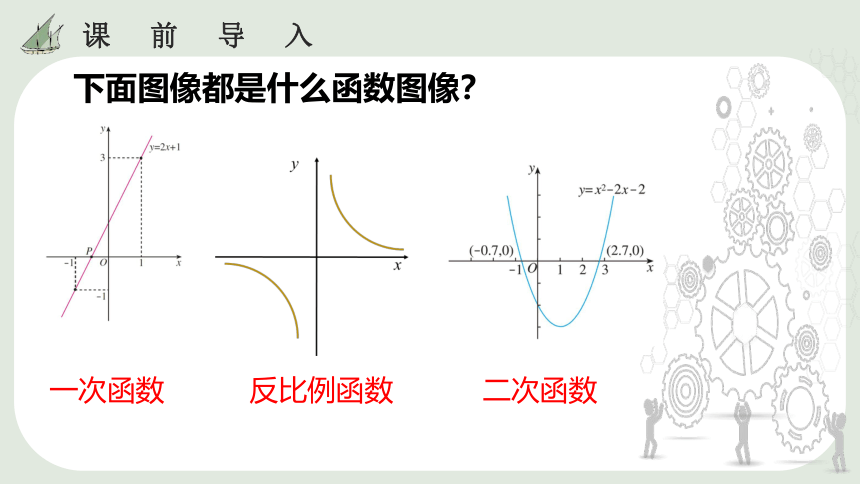
下面图像都是什么函数图像?
一次函数
反比例函数
二次函数
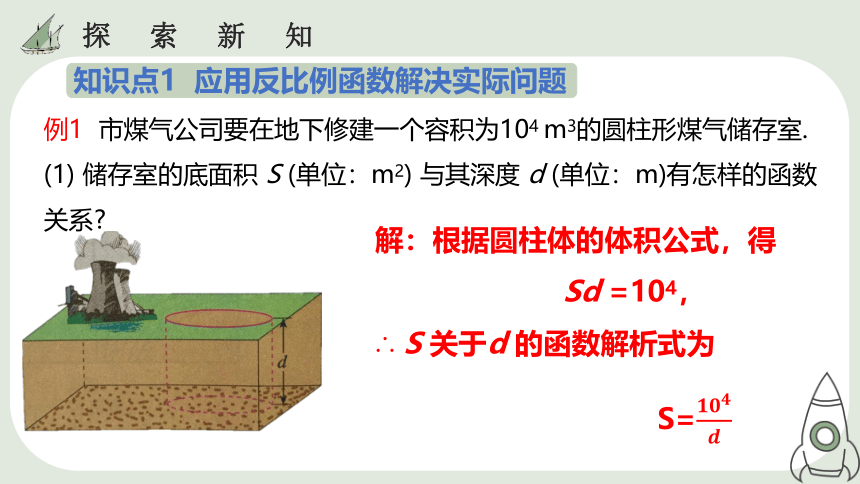
例1 市煤气公司要在地下修建一个容积为104 m3的圆柱形煤气储存室.
(1) 储存室的底面积 S (单位:m2) 与其深度 d (单位:m)有怎样的函数关系
知识点1 应用反比例函数解决实际问题
解:根据圆柱体的体积公式,得
Sd =104,
∴ S 关于d 的函数解析式为
S=
解:把 S = 500 代入 S=,得
500=
解得 d = 20.
如果把储存室的底面积定为 500 m ,施工时应向地下掘进 20 m 深.
(2) 公司决定把储存室的底面积 S 定为 500 m2,施工队施工时应该向下掘进多深
(3) 当施工队按(2)中的计划掘进到地下15m时,公司临时改变计划,把储存室的深度改为15m.相应地,储存室的底面积应改为多少(结果保留小数点后两位)
解:根据题意,把 d =15 代入 S=,得
S=
解得 S≈666.67.
当储存室的深度为15 m 时,底面积应改为 666.67 m .
例2 码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间.
(1) 轮船到达目的地后开始卸货,平均卸货速度v (单位:吨/天)与卸货天数 t 之间有怎样的函数关系
分析:根据平均装货速度×装货天数=货物的总量,可以求出轮
船装载货物的总量;
再根据平均卸货速度=货物的总量÷卸货天数,
得到 v 关于 t 的函数解析式.
(1) 轮船到达目的地后开始卸货,平均卸货速度v (单位:吨/天)与卸货天数 t 之间有怎样的函数关系
解:设轮船上的货物总量为 k 吨,根据已知条件得
k =30×8=240,
所以 v 关于 t 的函数解析式为
(2) 由于遇到紧急情况,要求船上的货物不超过 5天卸载完毕,那么平均每天至少要卸载多少吨
解:把 t =5 代入,得
=48
从结果可以看出,如果全部货物恰好用 5 天卸载完,则平均每天卸载 48 吨. 而观察可知,t 越小,v 越大. 这样若货物不超过 5 天卸载完,则平均每天至少要卸载 48 吨.
方法总结:在解决反比例函数相关的实际问题中,若题目要求“至多”、“至少”,可以利用反比例函数的增减性来解答 .
公元前 3 世纪,有一位科学家说了这样一句名言:“给我一个支点,我可以撬动地球!”你们知道这位科学家是谁吗?这里蕴含什么样的原理呢?
阿基米德
若杠杆上的两物体与支点的距离与其重量成反比,则杠杆平衡.后来人们把它归纳为“杠杆原理”.通俗地说,杠杆原理为:
阻力 × 阻力臂 = 动力 × 动力臂
阻力
动力
支点
动力臂
阻力臂
例3 小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为 1200 N 和 0.5 m.
(1) 动力 F 与动力臂 l 有怎样的函数关系 当动力臂为
1.5 m时,撬动石头至少需要多大的力
解:根据“杠杆原理”,得
∴ F 关于l 的函数解析式为
Fl =1200×0.5,
解:根据“杠杆原理”,得
∴ F 关于l 的函数解析式为
当 l=1.5m 时,
对于函数 ,当 l =1.5 m时,F =400 N,此时杠杆平衡.
因此撬动石头至少需要400N的力.
Fl =1200×0.5,
(2) 若想使动力 F 不超过题 (1) 中所用力的一半,则动力臂l至少要加长多少
提示:对于函数 ,F 随 l 的增大而减小. 因此,只要求出 F =200 N 时对应的 l 的值,就能确定动力臂 l 至少应加长的量.
3-1.5 =1.5 (m).
对于函数 ,当 l >0 时,l 越大,F越小. 因此,若想用力不超过 400 N 的一半,则动力臂至少要加长 1.5 m.
解:当F=400× =200 时,由200 = 得
电学知识告诉我们,用电器的功率 P(单位:W)、两端的电压 U(单位:V)以及用电器的电阻 R(单位: Ω )有如下关系 PR=U 2.这个关系
也可写为 P= ,或 R= .
例4 一个用电器的电阻是可调节的,其范围为 110~220 Ω. 已知电压为 220 V,这个用电器的电路图如图所示.
(1) 功率 P 与电阻 R 有怎样的函数关系
解:根据电学知识,
当 U = 220 时,得
U
~
(2) 这个用电器功率的范围是多少
解:根据反比例函数的性质可知,电阻越大,功率越小.
把电阻的最小值 R = 110 代入求得的解析式,
得到功率的最大值440
把电阻的最大值 R = 220 代入求得的解析式,
得到功率的最小值220
因此用电器功率的范围为220~440 W.
结合例4,想一想为什么收音机的音量、某些台灯的亮度以及电风扇的转速可以调节
收音机的音量、台灯的亮度以及电风扇的转速由用电器的功率决定.
练习1 如图,某玻璃器皿制造公司要制造一种容积为1升(1升=1立方分米)的圆锥形漏斗.
(1) 漏斗口的面积 S (单位:dm2)与漏斗的深 d (单位:dm) 有怎样的函数关系
d
解:
(2) 如果漏斗的深为10 cm,那么漏斗口的面积为多少 dm2?
解:10cm=1dm,把 d =1 代入解析式,得
S =3.
所以漏斗口的面积为 3 dm2.
练习2 一司机驾汽车从甲地去乙地,以 80 千米/小时的平均速度用 6 h到达目的地.
(1)当他按原路匀速返回时,汽车速度 v(千米/小时)与时间 t(小时)有怎样的函数关系?
(2)如果该司机必须在 4 h之内返回甲地,则返程时的速度不得低于多少?
120千米/小时
练习3 新建成的住宅楼主体工程已经竣工,只剩下楼体外表面需要贴瓷砖,已知楼体外表面的面积为5×103 m2.
(1)所需瓷砖的块数 n 与每块瓷砖的面积 S 有怎样的函数关系?
(2)为了使住宅楼的外观更漂亮,开发商决定采用灰、白和蓝三种颜色的瓷砖,每块砖的面积都是 80 cm2,灰、白、蓝瓷砖使用比例为2∶2∶1,则需三种瓷砖各多少块?
需灰、白、蓝三种瓷砖分别为2.5×105块、2.5×105块、1.25×105块.
练习4 如图,科技小组准备用材料围建一个面积为60 m2 的矩形科技园 ABCD,其中一边 AB 靠墙,墙长为 12 m,设 AD 的长为 x m,DC 的长为 y m.
(1)求 y 与 x 之间的函数关系式;
(2)若围成矩形科技园 ABCD 的三边材料总长不超过 26 m,材料 AD 和 DC 的长都是整米数,求出满足条件的所有围建方案.
AD = 5 m,DC = 12 m;AD = 6 m,DC = 10 m;AD =10 m,DC = 6 m.
实际生活与反比例函数
过程:
分析实际情境→建立函数模型→明确数学问题
特别注意:自变量和因变量的取值范围.
第二十六章 反比例函数
26.2 实际问题与反比例函数
主讲人:数学可以很简单
能够通过分析实际问题中变量之间的关系,
建立反比例函数模型解决问题,进一步提高运用函数的图象
、性质的综合能力. (重点、难点)
2. 能够根据实际问题确定自变量的取值范围.(重点)
下面图像都是什么函数图像?
一次函数
反比例函数
二次函数
例1 市煤气公司要在地下修建一个容积为104 m3的圆柱形煤气储存室.
(1) 储存室的底面积 S (单位:m2) 与其深度 d (单位:m)有怎样的函数关系
知识点1 应用反比例函数解决实际问题
解:根据圆柱体的体积公式,得
Sd =104,
∴ S 关于d 的函数解析式为
S=
解:把 S = 500 代入 S=,得
500=
解得 d = 20.
如果把储存室的底面积定为 500 m ,施工时应向地下掘进 20 m 深.
(2) 公司决定把储存室的底面积 S 定为 500 m2,施工队施工时应该向下掘进多深
(3) 当施工队按(2)中的计划掘进到地下15m时,公司临时改变计划,把储存室的深度改为15m.相应地,储存室的底面积应改为多少(结果保留小数点后两位)
解:根据题意,把 d =15 代入 S=,得
S=
解得 S≈666.67.
当储存室的深度为15 m 时,底面积应改为 666.67 m .
例2 码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间.
(1) 轮船到达目的地后开始卸货,平均卸货速度v (单位:吨/天)与卸货天数 t 之间有怎样的函数关系
分析:根据平均装货速度×装货天数=货物的总量,可以求出轮
船装载货物的总量;
再根据平均卸货速度=货物的总量÷卸货天数,
得到 v 关于 t 的函数解析式.
(1) 轮船到达目的地后开始卸货,平均卸货速度v (单位:吨/天)与卸货天数 t 之间有怎样的函数关系
解:设轮船上的货物总量为 k 吨,根据已知条件得
k =30×8=240,
所以 v 关于 t 的函数解析式为
(2) 由于遇到紧急情况,要求船上的货物不超过 5天卸载完毕,那么平均每天至少要卸载多少吨
解:把 t =5 代入,得
=48
从结果可以看出,如果全部货物恰好用 5 天卸载完,则平均每天卸载 48 吨. 而观察可知,t 越小,v 越大. 这样若货物不超过 5 天卸载完,则平均每天至少要卸载 48 吨.
方法总结:在解决反比例函数相关的实际问题中,若题目要求“至多”、“至少”,可以利用反比例函数的增减性来解答 .
公元前 3 世纪,有一位科学家说了这样一句名言:“给我一个支点,我可以撬动地球!”你们知道这位科学家是谁吗?这里蕴含什么样的原理呢?
阿基米德
若杠杆上的两物体与支点的距离与其重量成反比,则杠杆平衡.后来人们把它归纳为“杠杆原理”.通俗地说,杠杆原理为:
阻力 × 阻力臂 = 动力 × 动力臂
阻力
动力
支点
动力臂
阻力臂
例3 小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为 1200 N 和 0.5 m.
(1) 动力 F 与动力臂 l 有怎样的函数关系 当动力臂为
1.5 m时,撬动石头至少需要多大的力
解:根据“杠杆原理”,得
∴ F 关于l 的函数解析式为
Fl =1200×0.5,
解:根据“杠杆原理”,得
∴ F 关于l 的函数解析式为
当 l=1.5m 时,
对于函数 ,当 l =1.5 m时,F =400 N,此时杠杆平衡.
因此撬动石头至少需要400N的力.
Fl =1200×0.5,
(2) 若想使动力 F 不超过题 (1) 中所用力的一半,则动力臂l至少要加长多少
提示:对于函数 ,F 随 l 的增大而减小. 因此,只要求出 F =200 N 时对应的 l 的值,就能确定动力臂 l 至少应加长的量.
3-1.5 =1.5 (m).
对于函数 ,当 l >0 时,l 越大,F越小. 因此,若想用力不超过 400 N 的一半,则动力臂至少要加长 1.5 m.
解:当F=400× =200 时,由200 = 得
电学知识告诉我们,用电器的功率 P(单位:W)、两端的电压 U(单位:V)以及用电器的电阻 R(单位: Ω )有如下关系 PR=U 2.这个关系
也可写为 P= ,或 R= .
例4 一个用电器的电阻是可调节的,其范围为 110~220 Ω. 已知电压为 220 V,这个用电器的电路图如图所示.
(1) 功率 P 与电阻 R 有怎样的函数关系
解:根据电学知识,
当 U = 220 时,得
U
~
(2) 这个用电器功率的范围是多少
解:根据反比例函数的性质可知,电阻越大,功率越小.
把电阻的最小值 R = 110 代入求得的解析式,
得到功率的最大值440
把电阻的最大值 R = 220 代入求得的解析式,
得到功率的最小值220
因此用电器功率的范围为220~440 W.
结合例4,想一想为什么收音机的音量、某些台灯的亮度以及电风扇的转速可以调节
收音机的音量、台灯的亮度以及电风扇的转速由用电器的功率决定.
练习1 如图,某玻璃器皿制造公司要制造一种容积为1升(1升=1立方分米)的圆锥形漏斗.
(1) 漏斗口的面积 S (单位:dm2)与漏斗的深 d (单位:dm) 有怎样的函数关系
d
解:
(2) 如果漏斗的深为10 cm,那么漏斗口的面积为多少 dm2?
解:10cm=1dm,把 d =1 代入解析式,得
S =3.
所以漏斗口的面积为 3 dm2.
练习2 一司机驾汽车从甲地去乙地,以 80 千米/小时的平均速度用 6 h到达目的地.
(1)当他按原路匀速返回时,汽车速度 v(千米/小时)与时间 t(小时)有怎样的函数关系?
(2)如果该司机必须在 4 h之内返回甲地,则返程时的速度不得低于多少?
120千米/小时
练习3 新建成的住宅楼主体工程已经竣工,只剩下楼体外表面需要贴瓷砖,已知楼体外表面的面积为5×103 m2.
(1)所需瓷砖的块数 n 与每块瓷砖的面积 S 有怎样的函数关系?
(2)为了使住宅楼的外观更漂亮,开发商决定采用灰、白和蓝三种颜色的瓷砖,每块砖的面积都是 80 cm2,灰、白、蓝瓷砖使用比例为2∶2∶1,则需三种瓷砖各多少块?
需灰、白、蓝三种瓷砖分别为2.5×105块、2.5×105块、1.25×105块.
练习4 如图,科技小组准备用材料围建一个面积为60 m2 的矩形科技园 ABCD,其中一边 AB 靠墙,墙长为 12 m,设 AD 的长为 x m,DC 的长为 y m.
(1)求 y 与 x 之间的函数关系式;
(2)若围成矩形科技园 ABCD 的三边材料总长不超过 26 m,材料 AD 和 DC 的长都是整米数,求出满足条件的所有围建方案.
AD = 5 m,DC = 12 m;AD = 6 m,DC = 10 m;AD =10 m,DC = 6 m.
实际生活与反比例函数
过程:
分析实际情境→建立函数模型→明确数学问题
特别注意:自变量和因变量的取值范围.
