人教版数学九年级下册26.2实际问题与反比例函数课件 (共20张PPT)
文档属性
| 名称 | 人教版数学九年级下册26.2实际问题与反比例函数课件 (共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-10 12:30:37 | ||
图片预览







文档简介
(共20张PPT)
实际问题与反比例函数
——反比例函数与一次函数的交点问题
1、能够解决反比例函数与一次函数的交点问题。
2、体会“数”与“形”的相互转化,学习数形结合的思想方法,进一步提高对反比例函数相关知识的综合运用能力。
学习目标
考情分析
2021年第17题6分、2020年第18题8分、2019年第5题3分、2018年第17题、2017年第20题、2015年第21题均考查反比例函数与一次函数的综合,涉及解直角三角形、全等三角形的判定与四边形面积的计算等;2014年第19题考查反比例函数与三角形的综合;2013年第19题考查反比例函数与矩形的综合.
2.反比例函数 的图象一定经过点(-2,___ )。
4.如图,反比例函数的图象在第一象限内经过点A,过点A分别向x轴、y轴作垂线,垂足分别P、Q,若矩形APOQ的面积为10,则这个反比例函数的解析式为________。
8
3
1.若反比例函数 与一次函数y=2x+b都经过点(1,4),则kb= _
复习回顾
3.反比例函数y= 与一次函数y=x-1的图象的交点坐标是
(2,1),(-1,-2)
一、利用交点求函数解析式
例1:如图,已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y= 的图象的两个交点,直线AB与y轴交于点C。
(1)求反比例函数和一次函数的解析式;
典例解读
二、利用交点求图形面积
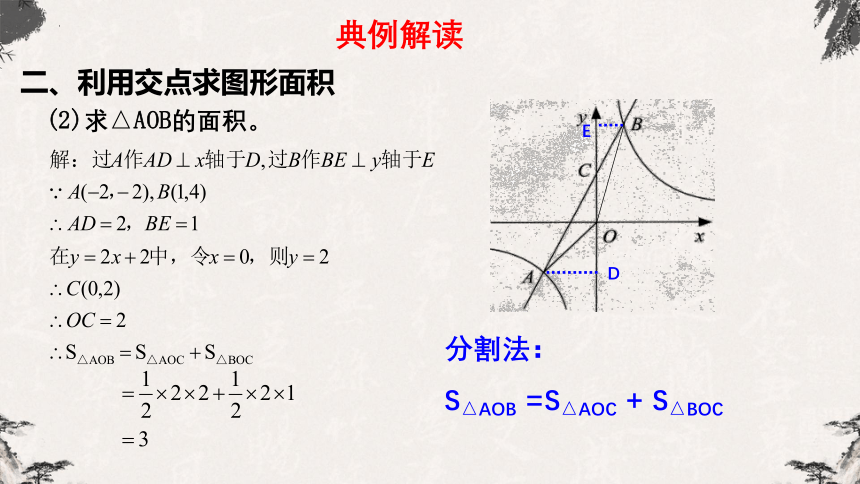
(2)求△AOB的面积。
分割法:
S△AOB =S△AOC + S△BOC
D
E
典例解读
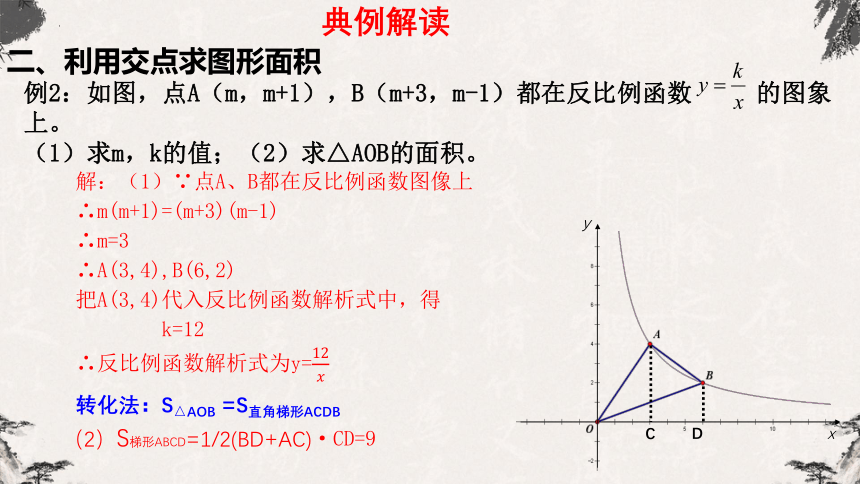
例2:如图,点A(m,m+1),B(m+3,m-1)都在反比例函数 的图象上。
(1)求m,k的值;(2)求△AOB的面积。
x
y
C
D
转化法:S△AOB =S直角梯形ACDB
二、利用交点求图形面积
典例解读
解:(1)∵点A、B都在反比例函数图像上
∴m(m+1)=(m+3)(m-1)
∴m=3
∴A(3,4),B(6,2)
把A(3,4)代入反比例函数解析式中,得
k=12
∴反比例函数解析式为y=
(2)S梯形ABCD=1/2(BD+AC)·CD=9
变式训练一
例4:如图,一次函数与反比例函数的图象相交于A、B两点,则图中使反比例函数的值小于一次函数的值的x的取值范围是( )
A.x<-1
B.x>2
C.-1<x<0,或x>2
D.x<-1,或0<x<2
-3
x
A
B
O
y
2
1
2
3
-1
-2
1
3
-3
-1
-2
①
②
③
④
c
三、利用交点求值或确定取值范围
典例解读
第1题图
(1)求反比例函数的解析式以及点C的坐标;
(2)点P是x轴上一动点,连接AP,若△ACP的面积是△AOB的面积的一半,求此时点P的坐标.
拓展提高
图3
第2题图
(1)直接写出一次函数与反比例函数的解析式;
(2)过点A作直线AC⊥x轴,垂足为点C,过点B的直线交x轴正半轴于点E,交直线AC于点F,若△ECF∽△ACD,求点E的坐标.
图4
如图,一次函数y1=kx+b的图象与反比例函数 的图象相交于A、B两点,且点A的横坐标和点B的纵坐标都是-2,直线AB与x轴交于点M。
求一次函数的解析式;
求△AOB的面积;
(3)根据图象写出使一次函数的值大于反比
例函数的值的x的取值范围。
B
M
O
A
y
x
-2
-2
4
4
(2,0)
课后作业
课堂小结
同学们,通过这节课的学习,你有什么收获呢?
1、求反比例函数及一次函数的解析式。
2、利用交点求面积问题。
3、利用交点求值或取值范围。
4、数学思想中的数形结合、相互转化思想。
实际问题与反比例函数
——反比例函数与一次函数的交点问题
1、能够解决反比例函数与一次函数的交点问题。
2、体会“数”与“形”的相互转化,学习数形结合的思想方法,进一步提高对反比例函数相关知识的综合运用能力。
学习目标
考情分析
2021年第17题6分、2020年第18题8分、2019年第5题3分、2018年第17题、2017年第20题、2015年第21题均考查反比例函数与一次函数的综合,涉及解直角三角形、全等三角形的判定与四边形面积的计算等;2014年第19题考查反比例函数与三角形的综合;2013年第19题考查反比例函数与矩形的综合.
2.反比例函数 的图象一定经过点(-2,___ )。
4.如图,反比例函数的图象在第一象限内经过点A,过点A分别向x轴、y轴作垂线,垂足分别P、Q,若矩形APOQ的面积为10,则这个反比例函数的解析式为________。
8
3
1.若反比例函数 与一次函数y=2x+b都经过点(1,4),则kb= _
复习回顾
3.反比例函数y= 与一次函数y=x-1的图象的交点坐标是
(2,1),(-1,-2)
一、利用交点求函数解析式
例1:如图,已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y= 的图象的两个交点,直线AB与y轴交于点C。
(1)求反比例函数和一次函数的解析式;
典例解读
二、利用交点求图形面积
(2)求△AOB的面积。
分割法:
S△AOB =S△AOC + S△BOC
D
E
典例解读
例2:如图,点A(m,m+1),B(m+3,m-1)都在反比例函数 的图象上。
(1)求m,k的值;(2)求△AOB的面积。
x
y
C
D
转化法:S△AOB =S直角梯形ACDB
二、利用交点求图形面积
典例解读
解:(1)∵点A、B都在反比例函数图像上
∴m(m+1)=(m+3)(m-1)
∴m=3
∴A(3,4),B(6,2)
把A(3,4)代入反比例函数解析式中,得
k=12
∴反比例函数解析式为y=
(2)S梯形ABCD=1/2(BD+AC)·CD=9
变式训练一
例4:如图,一次函数与反比例函数的图象相交于A、B两点,则图中使反比例函数的值小于一次函数的值的x的取值范围是( )
A.x<-1
B.x>2
C.-1<x<0,或x>2
D.x<-1,或0<x<2
-3
x
A
B
O
y
2
1
2
3
-1
-2
1
3
-3
-1
-2
①
②
③
④
c
三、利用交点求值或确定取值范围
典例解读
第1题图
(1)求反比例函数的解析式以及点C的坐标;
(2)点P是x轴上一动点,连接AP,若△ACP的面积是△AOB的面积的一半,求此时点P的坐标.
拓展提高
图3
第2题图
(1)直接写出一次函数与反比例函数的解析式;
(2)过点A作直线AC⊥x轴,垂足为点C,过点B的直线交x轴正半轴于点E,交直线AC于点F,若△ECF∽△ACD,求点E的坐标.
图4
如图,一次函数y1=kx+b的图象与反比例函数 的图象相交于A、B两点,且点A的横坐标和点B的纵坐标都是-2,直线AB与x轴交于点M。
求一次函数的解析式;
求△AOB的面积;
(3)根据图象写出使一次函数的值大于反比
例函数的值的x的取值范围。
B
M
O
A
y
x
-2
-2
4
4
(2,0)
课后作业
课堂小结
同学们,通过这节课的学习,你有什么收获呢?
1、求反比例函数及一次函数的解析式。
2、利用交点求面积问题。
3、利用交点求值或取值范围。
4、数学思想中的数形结合、相互转化思想。
