人教版数学九年级下册27.1 图形的相似 课件(共29张PPT)
文档属性
| 名称 | 人教版数学九年级下册27.1 图形的相似 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-10 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
第二十七章 相 似
人教版九年级(下)数学
27.1 图形的相似
全等图形
能够完全重合(即它们的形状和大小完全相同)的两个图形全等,
从今天开始我们学习一种新的图形关系---相似
“相似”和“全等”有着密切的关系,也有着重大的不同。
温故知新
学习目标
1. 了解相似图形和相似比的概念.
2.
3.理解相似多边形的定义.
3. 能根据多边形相似进行相关的计算,会根据条件
判断两个多边形是否相似. (重点、难点)
相似图形的概念
01
成比例的线段
02
相似多边形
03
知识点
镜子里的帅气的身影和狗蛋完全相同。
我还想让大家都知道我长得帅,有什么好办法?
李狗蛋是怎么知道自己长得帅?
这种图形关系就是我们今天要学习的
相似图形
因为它们的形状和狗蛋相同
可这些照片和狗蛋不一样大,为什么大家能认出这就是李狗蛋呢?
形状相同的图形叫相似图形.
两个图形相似,一个图形可以看作由另一个图形放大或缩小得到.
相似图形:
全等图形是特殊的相似图形,相似图形不一定是全等图形.
定义
全等图形:形状相同、大小相等的图形叫全等图形.
要点归纳
知识点一
相似图形的概念
图形的缩小
图形的放大
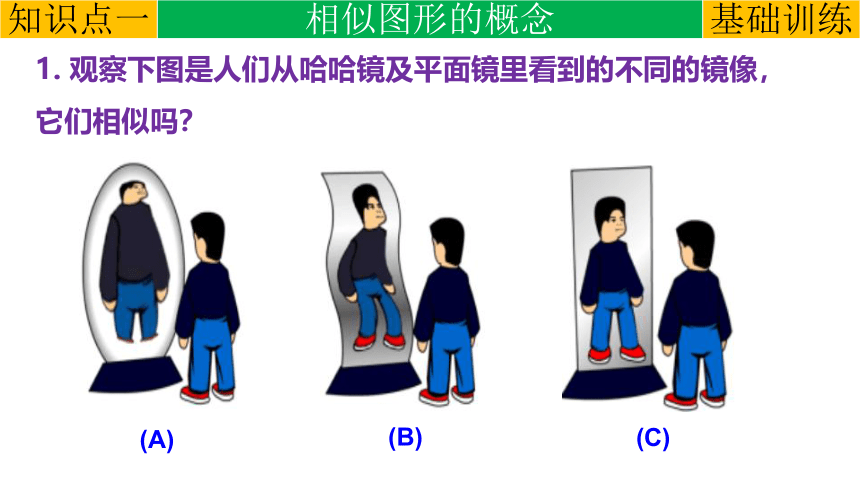
1. 观察下图是人们从哈哈镜及平面镜里看到的不同的镜像,它们相似吗?
(A)
(B)
(C)
基础训练
知识点一
相似图形的概念
2.观察下面的图形(a)~(g),其中哪些是与图形(1)、(2)或(3) 相似的
基础训练
知识点一
相似图形的概念
3.如图,从放大镜里看到的三角尺和原来的三角尺相似吗?
基础训练
知识点一
相似图形的概念
相似图形的概念
01
成比例的线段
02
相似多边形
03
知识点
1.线段的比:
在同一单位长度下,两条线段长度的比叫做两条线段的比。
已知:线段AB=1 m,CD=50 cm,则AB:CD=_____
1:50
要点归纳
知识点二
成比例的线段
在四条线段 a、b、c、d 中,如果 a 和 b 的比(即它们长度的比)等于 c 和 d 的比,那么这四条线段a、b、c、d 叫做成比例线段,简称 比例线段.
外项
外项
内项
内项
a :b = c :d.
外项
内项
a、b、c 的第四比例项
如果作为比例内项的是两条相等的线段即 或a :b = b :c,
那么线段 b 叫做线段 a 和 c 的比例中项.
要点归纳
知识点二
成比例的线段
例:线段m=1cm,n=2cm,p=3cm,q=6cm,请判断这四条线段成比例吗?并说明理由.
例题讲解
知识点二
成比例的线段
(1)a=2cm,b=4cm,c=3m,d=6m;
(2)a=1, b=6, c=2, d=3.
1.判断下列线段是否存在成比例线段
2.判断下列线段a、b、c、d是否是成比例线段
(1)a=2cm,b=4cm,c=3m,d=6m;
(2)a=1, b=6, c=2, d=3.
老师,太简单了我完成了
李狗蛋认为第1题都是成比例线段,因此第2题也都是
基础训练
知识点二
成比例的线段
相似图形的概念
01
成比例的线段
02
相似多边形
03
知识点
刚刚我们学习了相似图形,什么样的两个图形会相似
形状相同的两个图形相似,
H
E
G
F
A
C
D
B
下面这两个图形相似吗?
这该怎么判断?
探究新知
知识点三
相似多边形
李狗蛋印了两张的照片,分别为1寸和2寸,它们相似吗?
对应部分成比例
若把帅气的李狗蛋照片,换成两个四边形,该怎么判断它们相似。
四边成比例的两个四边形相似.
探究新知
知识点三
相似多边形
不对,仅有四边成比例,不能得出两个四边形相似,比如两个菱形就不一定相似.
那就四个角分别相等的两个四边形相似.
也不对,仅有四个角分别相等,不能得出两个四边形相似,比如两个矩形就不一定相似.
那就各角分别相等、各边成比例的两个四边形相似。
探究新知
知识点三
相似多边形
各角分别相等、各边成比例的两个多边形叫做相似多边形.
相似多边形的对应边的比叫作相似比.
相似多边形的对应角相等,对应边成比例.
相似比:
相似多边形的性质:
相似多边形的定义:
注意:(1)相似比与两个多边形的前后顺序有关;
(2)相似比为1的两个相似多边形为全等多边形。
要点归纳
知识点三
相似多边形
例: 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x
解:四边形ABCD和EFGH相似,它们的对应角相等.由此可得
四边形ABCD和EFGH相似,它们的对应边的比相等.由此可得
解得 x=28(cm)
∠α=∠C=83°,∠A=∠E=118°
在四边形ABCD中,∠β=360°-(78°+83°+118°)=81°.
D
A
B
C
18cm
21cm
78°
83°
β
24cm
G
E
F
H
α
x
118°
知识点三
典型例题
知识点三
相似多边形
1.若△ABC与△A B C 相似,且AB:A B =1:2,则△ABC与△A B C 的相似比是________,△A B C 与△ABC的相似比是_________.
1:2
2:1
基础训练
知识点三
相似多边形
注意:相似比与两个多边形的前后顺序有关;
2.如图,△ABC与△DEF相似,求未知边x,y的长度。
基础训练
知识点三
相似多边形
3.如图矩形草坪长20m,宽10m,沿草坪四周有1m宽的环形小路,小路内外边缘所成的矩形是否相似
基础训练
知识点三
相似多边形
本节课我们学了什么?
我们学习了相似图形的定义,
我们学习了
线段的比和
成比例的线段;
我们还学习了
相似多边形的
定义及性质,还有相似比
课堂小结
强 化 训 练
OPTION
1.如图是两个相似的矩形,右边的矩形一边为15,它的邻边为__________.
22.5或10
30
20
强化训练
2. 已知 ,求 的值吗?
已知a,b,c,d,......e,f
如果 ,
那么 .
(等比性质)
强化训练
3.任意两个等边三角形相似吗 任意两个正方形呢 任意两个正n边形呢 任意的两个菱形(或矩形)是否相似?
a1
a2
a3
an
…
…
a1
a2
a3
an
归纳:任意两个边数相等的正多边形都相似.
强化训练
第二十七章 相 似
人教版九年级(下)数学
27.1 图形的相似
全等图形
能够完全重合(即它们的形状和大小完全相同)的两个图形全等,
从今天开始我们学习一种新的图形关系---相似
“相似”和“全等”有着密切的关系,也有着重大的不同。
温故知新
学习目标
1. 了解相似图形和相似比的概念.
2.
3.理解相似多边形的定义.
3. 能根据多边形相似进行相关的计算,会根据条件
判断两个多边形是否相似. (重点、难点)
相似图形的概念
01
成比例的线段
02
相似多边形
03
知识点
镜子里的帅气的身影和狗蛋完全相同。
我还想让大家都知道我长得帅,有什么好办法?
李狗蛋是怎么知道自己长得帅?
这种图形关系就是我们今天要学习的
相似图形
因为它们的形状和狗蛋相同
可这些照片和狗蛋不一样大,为什么大家能认出这就是李狗蛋呢?
形状相同的图形叫相似图形.
两个图形相似,一个图形可以看作由另一个图形放大或缩小得到.
相似图形:
全等图形是特殊的相似图形,相似图形不一定是全等图形.
定义
全等图形:形状相同、大小相等的图形叫全等图形.
要点归纳
知识点一
相似图形的概念
图形的缩小
图形的放大
1. 观察下图是人们从哈哈镜及平面镜里看到的不同的镜像,它们相似吗?
(A)
(B)
(C)
基础训练
知识点一
相似图形的概念
2.观察下面的图形(a)~(g),其中哪些是与图形(1)、(2)或(3) 相似的
基础训练
知识点一
相似图形的概念
3.如图,从放大镜里看到的三角尺和原来的三角尺相似吗?
基础训练
知识点一
相似图形的概念
相似图形的概念
01
成比例的线段
02
相似多边形
03
知识点
1.线段的比:
在同一单位长度下,两条线段长度的比叫做两条线段的比。
已知:线段AB=1 m,CD=50 cm,则AB:CD=_____
1:50
要点归纳
知识点二
成比例的线段
在四条线段 a、b、c、d 中,如果 a 和 b 的比(即它们长度的比)等于 c 和 d 的比,那么这四条线段a、b、c、d 叫做成比例线段,简称 比例线段.
外项
外项
内项
内项
a :b = c :d.
外项
内项
a、b、c 的第四比例项
如果作为比例内项的是两条相等的线段即 或a :b = b :c,
那么线段 b 叫做线段 a 和 c 的比例中项.
要点归纳
知识点二
成比例的线段
例:线段m=1cm,n=2cm,p=3cm,q=6cm,请判断这四条线段成比例吗?并说明理由.
例题讲解
知识点二
成比例的线段
(1)a=2cm,b=4cm,c=3m,d=6m;
(2)a=1, b=6, c=2, d=3.
1.判断下列线段是否存在成比例线段
2.判断下列线段a、b、c、d是否是成比例线段
(1)a=2cm,b=4cm,c=3m,d=6m;
(2)a=1, b=6, c=2, d=3.
老师,太简单了我完成了
李狗蛋认为第1题都是成比例线段,因此第2题也都是
基础训练
知识点二
成比例的线段
相似图形的概念
01
成比例的线段
02
相似多边形
03
知识点
刚刚我们学习了相似图形,什么样的两个图形会相似
形状相同的两个图形相似,
H
E
G
F
A
C
D
B
下面这两个图形相似吗?
这该怎么判断?
探究新知
知识点三
相似多边形
李狗蛋印了两张的照片,分别为1寸和2寸,它们相似吗?
对应部分成比例
若把帅气的李狗蛋照片,换成两个四边形,该怎么判断它们相似。
四边成比例的两个四边形相似.
探究新知
知识点三
相似多边形
不对,仅有四边成比例,不能得出两个四边形相似,比如两个菱形就不一定相似.
那就四个角分别相等的两个四边形相似.
也不对,仅有四个角分别相等,不能得出两个四边形相似,比如两个矩形就不一定相似.
那就各角分别相等、各边成比例的两个四边形相似。
探究新知
知识点三
相似多边形
各角分别相等、各边成比例的两个多边形叫做相似多边形.
相似多边形的对应边的比叫作相似比.
相似多边形的对应角相等,对应边成比例.
相似比:
相似多边形的性质:
相似多边形的定义:
注意:(1)相似比与两个多边形的前后顺序有关;
(2)相似比为1的两个相似多边形为全等多边形。
要点归纳
知识点三
相似多边形
例: 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x
解:四边形ABCD和EFGH相似,它们的对应角相等.由此可得
四边形ABCD和EFGH相似,它们的对应边的比相等.由此可得
解得 x=28(cm)
∠α=∠C=83°,∠A=∠E=118°
在四边形ABCD中,∠β=360°-(78°+83°+118°)=81°.
D
A
B
C
18cm
21cm
78°
83°
β
24cm
G
E
F
H
α
x
118°
知识点三
典型例题
知识点三
相似多边形
1.若△ABC与△A B C 相似,且AB:A B =1:2,则△ABC与△A B C 的相似比是________,△A B C 与△ABC的相似比是_________.
1:2
2:1
基础训练
知识点三
相似多边形
注意:相似比与两个多边形的前后顺序有关;
2.如图,△ABC与△DEF相似,求未知边x,y的长度。
基础训练
知识点三
相似多边形
3.如图矩形草坪长20m,宽10m,沿草坪四周有1m宽的环形小路,小路内外边缘所成的矩形是否相似
基础训练
知识点三
相似多边形
本节课我们学了什么?
我们学习了相似图形的定义,
我们学习了
线段的比和
成比例的线段;
我们还学习了
相似多边形的
定义及性质,还有相似比
课堂小结
强 化 训 练
OPTION
1.如图是两个相似的矩形,右边的矩形一边为15,它的邻边为__________.
22.5或10
30
20
强化训练
2. 已知 ,求 的值吗?
已知a,b,c,d,......e,f
如果 ,
那么 .
(等比性质)
强化训练
3.任意两个等边三角形相似吗 任意两个正方形呢 任意两个正n边形呢 任意的两个菱形(或矩形)是否相似?
a1
a2
a3
an
…
…
a1
a2
a3
an
归纳:任意两个边数相等的正多边形都相似.
强化训练
