人教版数学九年级下册27.2.2 相似三角形的性质 课件(共21张PPT)
文档属性
| 名称 | 人教版数学九年级下册27.2.2 相似三角形的性质 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 505.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-10 12:19:21 | ||
图片预览

文档简介
(共21张PPT)
27.2.2 相似三角形的性质
【人教版 数学 九年(下)第27章 相似】
情境引入
三角形中有各种各样的几何量.
三条边的长度
三个内角的度数
周长、面积等等
高、中线、角平分线的长度
如:
如果两个三角形相似,那么它们的这些几何量之间有什么关系呢?
探究归纳
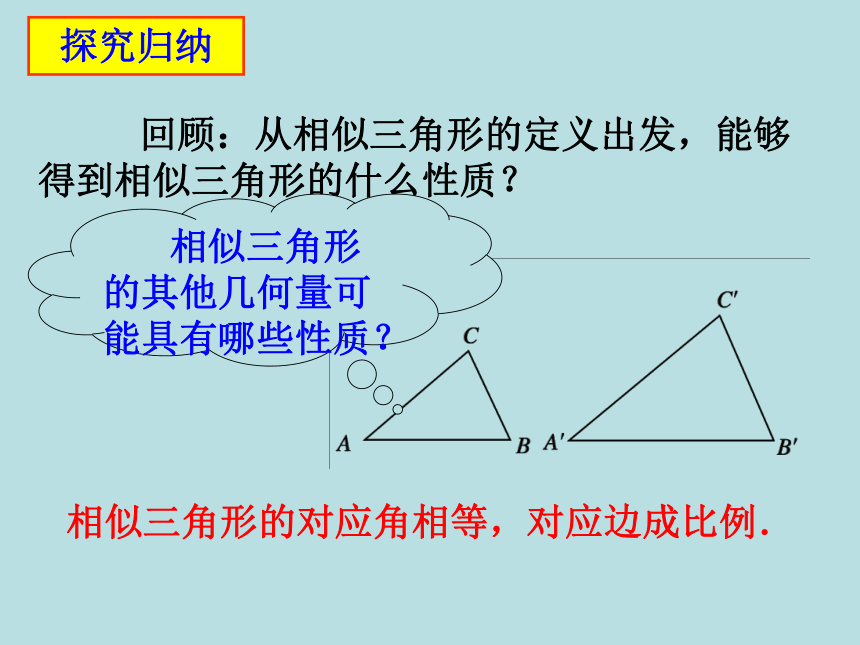
回顾:从相似三角形的定义出发,能够得到相似三角形的什么性质?
相似三角形的对应角相等,对应边成比例.
相似三角形的其他几何量可能具有哪些性质?
探究归纳
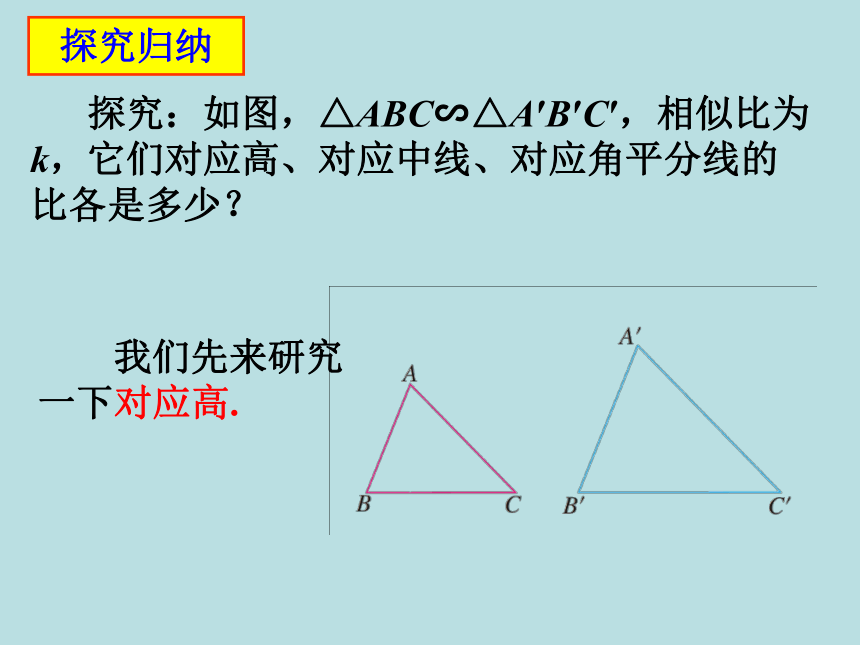
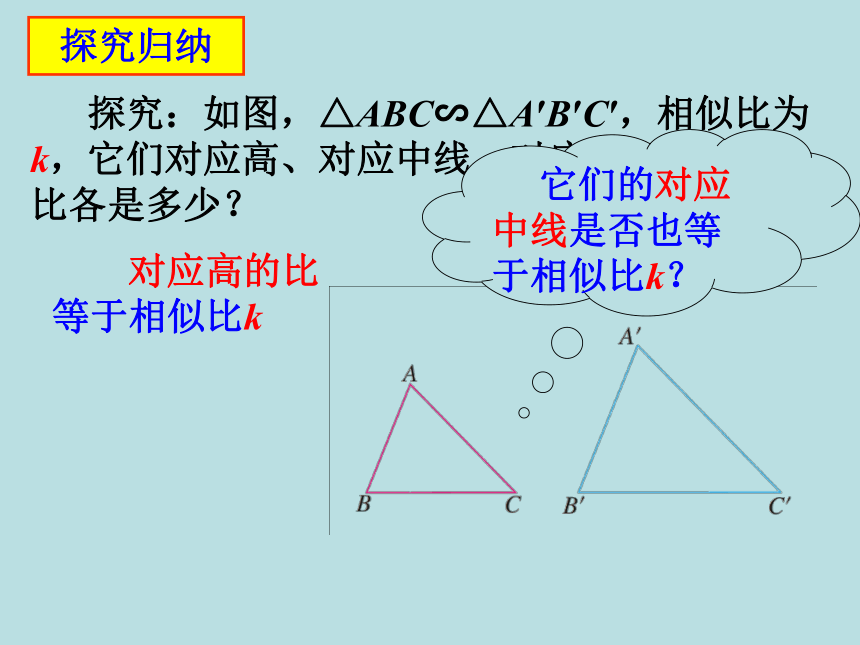
探究:如图,△ABC∽△A′B′C′,相似比为k,它们对应高、对应中线、对应角平分线的比各是多少?
我们先来研究一下对应高.
探究归纳
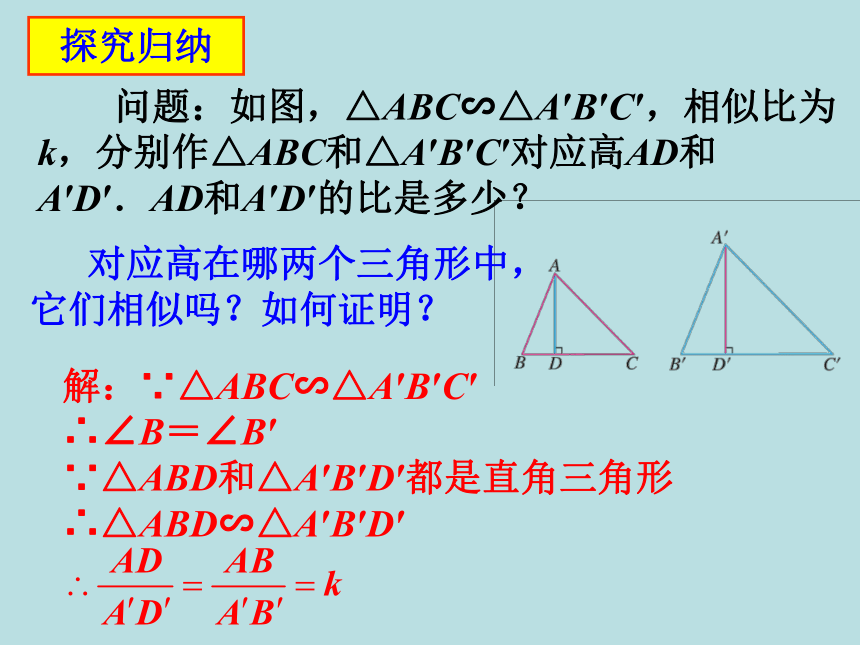
问题:如图,△ABC∽△A′B′C′,相似比为k,分别作△ABC和△A′B′C′对应高AD和A′D′.AD和A′D′的比是多少?
解:∵△ABC∽△A′B′C′
∴∠B=∠B′
∵△ABD和△A′B′D′都是直角三角形
∴△ABD∽△A′B′D′
对应高在哪两个三角形中,
它们相似吗?如何证明?
探究归纳
探究:如图,△ABC∽△A′B′C′,相似比为k,它们对应高、对应中线、对应角平分线的比各是多少?
对应高的比等于相似比k
它们的对应中线是否也等于相似比k?
探究归纳
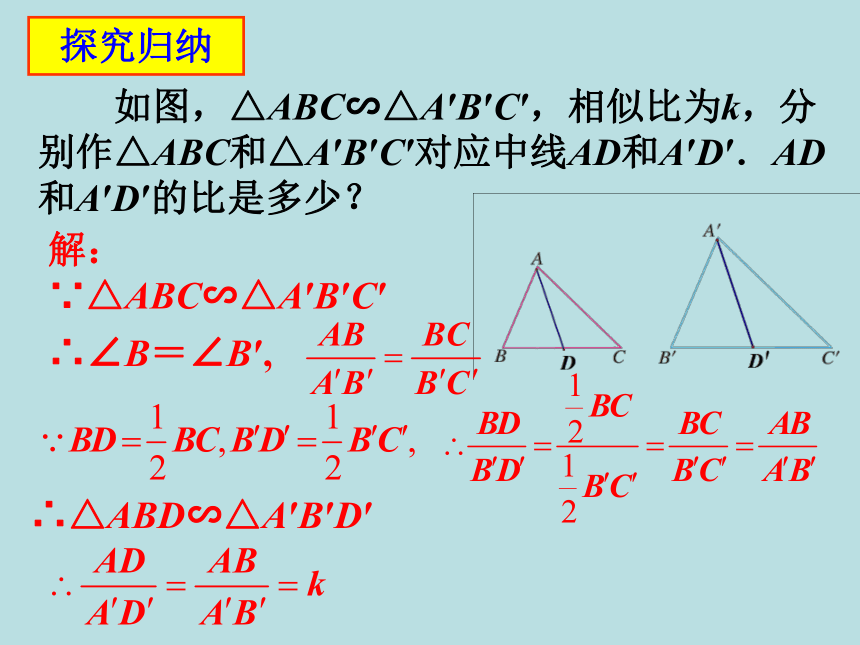
如图,△ABC∽△A′B′C′,相似比为k,分别作△ABC和△A′B′C′对应中线AD和A′D′.AD和A′D′的比是多少?
解:
∵△ABC∽△A′B′C′
∴∠B=∠B′,
∴△ABD∽△A′B′D′
探究归纳
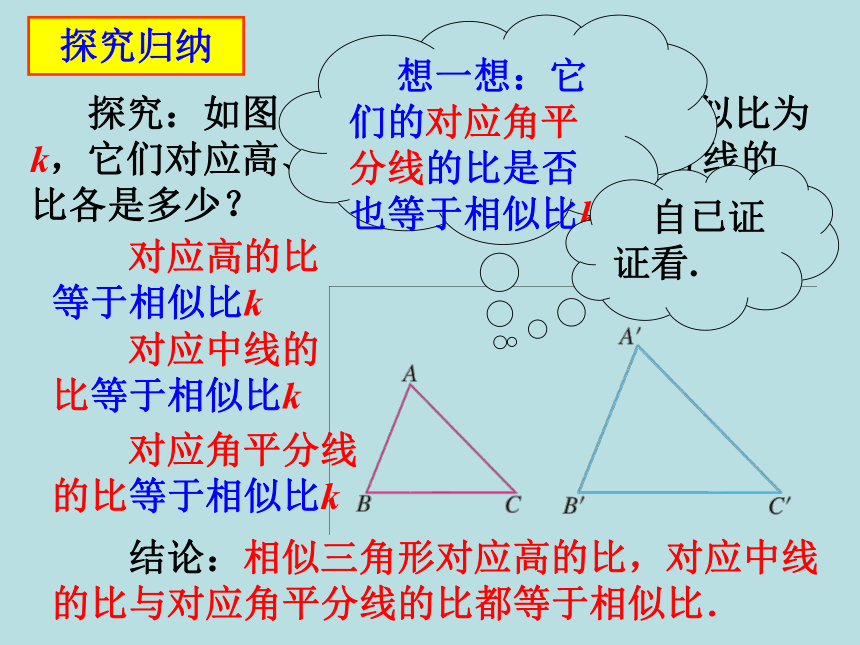
探究:如图,△ABC∽△A′B′C′,相似比为k,它们对应高、对应中线、对应角平分线的比各是多少?
对应高的比等于相似比k
对应中线的比等于相似比k
对应角平分线的比等于相似比k
结论:相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
想一想:它们的对应角平分线的比是否也等于相似比k?
自已证证看.
探究归纳
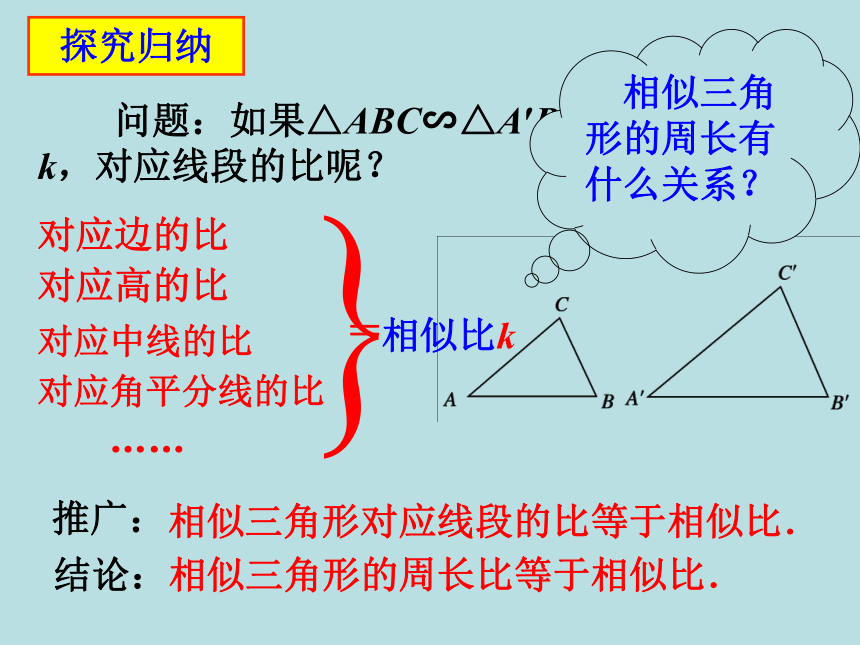
问题:如果△ABC∽△A′B′C′,相似比为k,对应线段的比呢?
相似三角形对应线段的比等于相似比.
对应边的比
相似比k
对应高的比
对应中线的比
对应角平分线的比
……
=
推广:
相似三角形的周长有什么关系?
结论:相似三角形的周长比等于相似比.
探究归纳
思考:相似三角形面积比与相似比有什么关系?
如图,△ABC∽
△A′B′C′,相似比为k,分别作△ABC和△A′B′C′对应高AD和A′D′.
结论:相似三角形面积比等于相似比的平方.
应用提高
例:如图,在△ABC 和△DEF 中,AB=2DE,
AC=2DF,∠A=∠D.若△ABC 的边 BC 上的高是6,面积为 ,求△DEF 的边 EF上的高和面积.
解:在△ABC 和△DEF 中,
∵AB=2DE,AC=2DF,
∵∠A=∠D,
∴△DEF∽△ABC,△DEF与△ABC的相似比为
∵△ABC 的边 BC 上的高是6,面积为 ,
∴△DEF的边 EF 上的高为
面积为
应用提高
1.判断
(1)一个三角形的各边长扩大为原来的5倍,这个三角形的角平分线也扩大为原来的5倍; ( )
(2)一个三角形的各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍. ( )
√
×
应用提高
2.如图,△ABC与△A′B′C′相似,AD、BE是的△ABC高,A′D′、B′E′是的△A′B′C′高,求证
∵△ABC∽△A′B′C′,
且AD与A′D′、 BE与 B′E′是对应高,
解:设△ABC与△A′B′C′的相似比为k
应用提高
3.在一张复印出来的纸上,一个三角形的一条边由原来的2cm变成了6cm,放缩比例是多少?这个三角形的面积发生了怎样的变化?
∴放缩比例是300%
解:∵6:2=3
∵32=9
∴面积扩大为原来的9倍
体验收获
说一说你的收获 ……
1.相似三角形对应角相等,
对应边成比例(对应边的比等于相似比)
2.相似三角形对应高线、对应中线、对应角平分线的比等于相似比
推广:相似三角形对应线段的比等于相似比
3.相似三角形对应周长比等于相似比
4.相似三角形对应面积比等于相似比的平方
设两个三角形的面积分别是4x,9x,根据题意得:
拓展提升
1.两个相似三角形的周长之比是2:3,它们的面积之差是60cm2 ,那么它们的面积之和是多少?
解得 x=12,
9x﹣4x=60
∴它们的面积之比是4:9.
解:∵两个三角形的周长之比是2:3,
∴它们的相似比是2:3,
∴9x+4x=156
答:它们的面积之和是156cm2.
拓展提升
2.如图,这是比例尺为1:1000的一块三角形草坪的图形,则草坪的实际面积是多少?
∴它们的面积之比是
1:1000000.
解:∵比例尺为1:1000,
∵图上草坪面积为:
∴草坪面积实际面积为:
(cm2)
3×1000000=3000000(cm2)=300(cm2)
拓展提升
3.如图,△ABC 的面积为 100,周长为 80,AB=20,点 D 是 AB 上一点,BD=12,过点 D 作 DE∥BC,交 AC于点 E.(1)求△ADE 的周长和面积;(2)过点 E 作 EF∥AB,EF 交 BC 于点 F,求△EFC 和四边形 DBFE 的面积.
(1)△ADE 的周长是32,面积16.
(2)△ EFC 的面积36.
四边形 DBFE 的面积48.
课内检测
1.用放大镜看一个三角形,一条边由原来的1cm变成5cm,那么看到的图案面积是原来的( )
A.5倍 B.15倍 C.25倍 D.30倍
2.两个等腰直角三角形的斜边比为1:2,则它们的周长比为( )
A.1:1 B.1:2 C.1:4 D.1:
3. 两个相似三角形最长边分别是20cm和16cm,它们的周长之和为90cm,则较大三角形的周长为( )
A.40cm B.50 cm C.60 cm D.70 cm
C
B
B
课内检测
4.两个相似三角的对应高分别为6cm和4cm,则这两个三角形的周长比为________,面积比为________.
5.已知两个相似三角形面积之比为9:25,其中一个周长为36,则另一个的周长为____________.
3:2
9:4
60或21.6
布置作业
必做题:
选做题:
教材42页习题27.2第6题.
教材43页习题27.2第12题.
27.2.2 相似三角形的性质
【人教版 数学 九年(下)第27章 相似】
情境引入
三角形中有各种各样的几何量.
三条边的长度
三个内角的度数
周长、面积等等
高、中线、角平分线的长度
如:
如果两个三角形相似,那么它们的这些几何量之间有什么关系呢?
探究归纳
回顾:从相似三角形的定义出发,能够得到相似三角形的什么性质?
相似三角形的对应角相等,对应边成比例.
相似三角形的其他几何量可能具有哪些性质?
探究归纳
探究:如图,△ABC∽△A′B′C′,相似比为k,它们对应高、对应中线、对应角平分线的比各是多少?
我们先来研究一下对应高.
探究归纳
问题:如图,△ABC∽△A′B′C′,相似比为k,分别作△ABC和△A′B′C′对应高AD和A′D′.AD和A′D′的比是多少?
解:∵△ABC∽△A′B′C′
∴∠B=∠B′
∵△ABD和△A′B′D′都是直角三角形
∴△ABD∽△A′B′D′
对应高在哪两个三角形中,
它们相似吗?如何证明?
探究归纳
探究:如图,△ABC∽△A′B′C′,相似比为k,它们对应高、对应中线、对应角平分线的比各是多少?
对应高的比等于相似比k
它们的对应中线是否也等于相似比k?
探究归纳
如图,△ABC∽△A′B′C′,相似比为k,分别作△ABC和△A′B′C′对应中线AD和A′D′.AD和A′D′的比是多少?
解:
∵△ABC∽△A′B′C′
∴∠B=∠B′,
∴△ABD∽△A′B′D′
探究归纳
探究:如图,△ABC∽△A′B′C′,相似比为k,它们对应高、对应中线、对应角平分线的比各是多少?
对应高的比等于相似比k
对应中线的比等于相似比k
对应角平分线的比等于相似比k
结论:相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
想一想:它们的对应角平分线的比是否也等于相似比k?
自已证证看.
探究归纳
问题:如果△ABC∽△A′B′C′,相似比为k,对应线段的比呢?
相似三角形对应线段的比等于相似比.
对应边的比
相似比k
对应高的比
对应中线的比
对应角平分线的比
……
=
推广:
相似三角形的周长有什么关系?
结论:相似三角形的周长比等于相似比.
探究归纳
思考:相似三角形面积比与相似比有什么关系?
如图,△ABC∽
△A′B′C′,相似比为k,分别作△ABC和△A′B′C′对应高AD和A′D′.
结论:相似三角形面积比等于相似比的平方.
应用提高
例:如图,在△ABC 和△DEF 中,AB=2DE,
AC=2DF,∠A=∠D.若△ABC 的边 BC 上的高是6,面积为 ,求△DEF 的边 EF上的高和面积.
解:在△ABC 和△DEF 中,
∵AB=2DE,AC=2DF,
∵∠A=∠D,
∴△DEF∽△ABC,△DEF与△ABC的相似比为
∵△ABC 的边 BC 上的高是6,面积为 ,
∴△DEF的边 EF 上的高为
面积为
应用提高
1.判断
(1)一个三角形的各边长扩大为原来的5倍,这个三角形的角平分线也扩大为原来的5倍; ( )
(2)一个三角形的各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍. ( )
√
×
应用提高
2.如图,△ABC与△A′B′C′相似,AD、BE是的△ABC高,A′D′、B′E′是的△A′B′C′高,求证
∵△ABC∽△A′B′C′,
且AD与A′D′、 BE与 B′E′是对应高,
解:设△ABC与△A′B′C′的相似比为k
应用提高
3.在一张复印出来的纸上,一个三角形的一条边由原来的2cm变成了6cm,放缩比例是多少?这个三角形的面积发生了怎样的变化?
∴放缩比例是300%
解:∵6:2=3
∵32=9
∴面积扩大为原来的9倍
体验收获
说一说你的收获 ……
1.相似三角形对应角相等,
对应边成比例(对应边的比等于相似比)
2.相似三角形对应高线、对应中线、对应角平分线的比等于相似比
推广:相似三角形对应线段的比等于相似比
3.相似三角形对应周长比等于相似比
4.相似三角形对应面积比等于相似比的平方
设两个三角形的面积分别是4x,9x,根据题意得:
拓展提升
1.两个相似三角形的周长之比是2:3,它们的面积之差是60cm2 ,那么它们的面积之和是多少?
解得 x=12,
9x﹣4x=60
∴它们的面积之比是4:9.
解:∵两个三角形的周长之比是2:3,
∴它们的相似比是2:3,
∴9x+4x=156
答:它们的面积之和是156cm2.
拓展提升
2.如图,这是比例尺为1:1000的一块三角形草坪的图形,则草坪的实际面积是多少?
∴它们的面积之比是
1:1000000.
解:∵比例尺为1:1000,
∵图上草坪面积为:
∴草坪面积实际面积为:
(cm2)
3×1000000=3000000(cm2)=300(cm2)
拓展提升
3.如图,△ABC 的面积为 100,周长为 80,AB=20,点 D 是 AB 上一点,BD=12,过点 D 作 DE∥BC,交 AC于点 E.(1)求△ADE 的周长和面积;(2)过点 E 作 EF∥AB,EF 交 BC 于点 F,求△EFC 和四边形 DBFE 的面积.
(1)△ADE 的周长是32,面积16.
(2)△ EFC 的面积36.
四边形 DBFE 的面积48.
课内检测
1.用放大镜看一个三角形,一条边由原来的1cm变成5cm,那么看到的图案面积是原来的( )
A.5倍 B.15倍 C.25倍 D.30倍
2.两个等腰直角三角形的斜边比为1:2,则它们的周长比为( )
A.1:1 B.1:2 C.1:4 D.1:
3. 两个相似三角形最长边分别是20cm和16cm,它们的周长之和为90cm,则较大三角形的周长为( )
A.40cm B.50 cm C.60 cm D.70 cm
C
B
B
课内检测
4.两个相似三角的对应高分别为6cm和4cm,则这两个三角形的周长比为________,面积比为________.
5.已知两个相似三角形面积之比为9:25,其中一个周长为36,则另一个的周长为____________.
3:2
9:4
60或21.6
布置作业
必做题:
选做题:
教材42页习题27.2第6题.
教材43页习题27.2第12题.
