27.2.3 相似三角形应用举例 课件(共25张PPT)
文档属性
| 名称 | 27.2.3 相似三角形应用举例 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-12 22:00:22 | ||
图片预览







文档简介
(共25张PPT)
第二十七章 相似
27.2 相似三角形
27.2.3 相似三角形应用举例
主讲人:数学可以很简单
1. 能够利用相似三角形的知识,求出不能直接测量
的物体的高度和宽度. (重点)
2. 进一步了解数学建模思想,能够将实际问题转化
为相似三角形的数学模型,提高分析问题、解决
问题的能力. (难点)
上海中心大厦
四川乐山大佛
黄河
今天我们就来学习利用相似三角形可以解决一些不能直接测量的物体的高度及两物之间的距离问题.
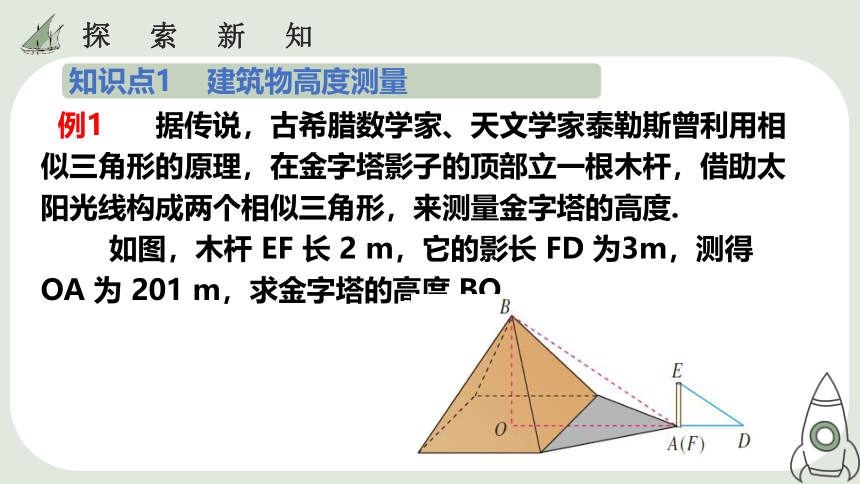
知识点1 建筑物高度测量
例1 据传说,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.
如图,木杆 EF 长 2 m,它的影长 FD 为3m,测得 OA 为 201 m,求金字塔的高度 BO.
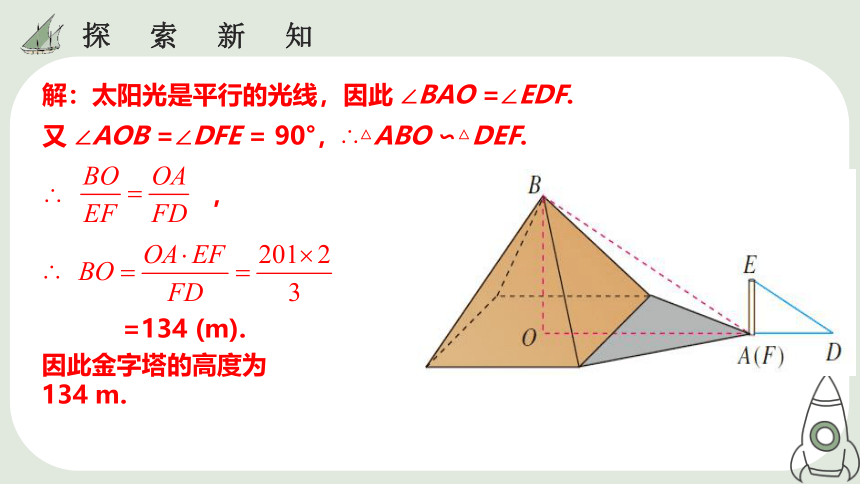
解:太阳光是平行的光线,因此 ∠BAO =∠EDF.
又 ∠AOB =∠DFE = 90°,∴△ABO ∽△DEF.
∴ ,
∴
=134 (m).
因此金字塔的高度为
134 m.
表达式:物1高 :物2高 = 影1长 :影2长
测量不能到达顶部的物体的高度,可以用“在同一时刻物高与影长成正比例”的原理解决.
方法总结:
小明身高 1.5 米,在操场的影长为 2 米,同时测得教学大楼在操场的影长为 60 米,则教学大楼的高度应为 ( )
A. 45米 B. 40米 C. 90米 D. 80米
A
知识点2 河流宽度的测量
例2 如图,为了估算河的宽度,我们可以在河对岸选定一个目标点 P,在近岸取点 Q 和 S,使点 P,Q,S 共线且直线 PS 与河垂直,接着在过点 S 且与 PS 垂直的直线 a 上选择适当的点 T,确定 PT 与过点 Q 且垂直 PS 的直线 b 的交点 R。已测得 QS = 45 m,ST = 90 m,QR = 60 m,请根据这些数据,计算河宽 PQ。
解:∵ ∠PQR=∠PST=90°,∠P=∠P,
∴ △PQR∽△PST. ∴
即 , ,
PQ×90=(PQ+45)×60.
解得 PQ=90(m).
因此,河宽大约为 90 m.
测量如河宽等不易直接测量的物体的宽度,常构造相似三角形求解.
方法总结:
如图,为了测量水塘边 A、B 两点之间的距离,在可以看到 A、B 的点 E 处,取 AE、BE 延长线上的 C、D 两点,使得 CD∥AB. 若测得 CD=5 m,AD=15m,ED=3 m,则 A、B 两点间的距离为 m.
A
B
E
D
C
20
知识点3 有遮挡物问题
例3 如图,左、右并排的两棵大树的高分别是 AB = 8 m 和 CD = 12 m,两树底部的距离 BD = 5 m,一个人估计自己眼睛距离地面 1.6 m,她沿着正对这两棵树的一条水平直路 l 从左向右前进,当她与左边较低的树的距离小于多少时,就看不到右边较高的树的顶端C 了
分析:如图,设观察者眼睛的位置 (视点) 为点 F,画出观察者的水平视线 FG,它交 AB,CD 于点 H,K.视线 FA,FG 的夹角 ∠AFH 是观察点 A 的仰角. 类似地,∠CFK 是观察点 C 时的仰角,由于树的遮挡,区域Ⅰ和Ⅱ都在观察者看不到的区域 (盲区) 之内. 再往前走就根本看不到 C 点了.
由此可知,如果观察者继续前进,当她与左边的树的距离小于 8 m 时,由于这棵树的遮挡,就看不到右边树的顶端 C .
解:如图,假设观察者从左向右走到点 E 时,她的眼
睛的位置点 E 与两棵树的顶端点 A,C 恰在一条
直线上.
∵AB⊥l,CD⊥l,∴AB∥CD.
∴△AEH∽△CEK.
即
解得:EH=8(m)
已知零件的外径为25 cm,要求它的厚度x,需先求出它的内孔直径AB,现用一个交叉卡钳(AC和BD的长相等)去量(如图),若OA∶OC=OB∶OD=3,CD=7 cm.
求此零件的厚度.
解:∵ ,
而∠AOB=∠COD,
∴△AOB∽△COD.
∴
又∵CD=7 cm,∴AB=21 cm.
由题意和图易知 25-2x=21,∴x=2(cm).
∴此零件的厚度为2 cm.
练习1 在某一时刻,测得一根长为1.8 m的竹竿的影长为3 m,同时测得一栋高楼的影长为90 m,这栋高楼的高度为多少?
x = 54m
解:设这栋高楼的高度为x.
练习2 如图,测得BD=120 m,DC=60 m,EC=50 m,求河宽AB。
解:∵∠ABD=∠ECD=90°,∠ADB=∠EDC,
∴△ABD∽△ECD.
∴
即. 解得AB=100(m)
练习3 如图,某一时刻,旗杆 AB 的影子的一部分在地面上,另一部分在建筑物的墙面上.小明测得旗杆AB 在地面上的影长 BC 为 9.6 m,在墙面上的影长 CD 为 2 m.同一时刻,小明又测得竖立于地面长 1 m 的标杆的影长为 1.2 m.请帮助小明求出旗杆的高度.
A
B
C
D
解:如图:过点 D 作 DE∥BC,交 AB 于点 E,
∴ DE = CB = 9.6 m,BE = CD = 2 m,
∵ 在同一时刻物高与影长成正比例,
∴ EA : ED=1 : 1.2,
∴ AE = 8 m,
∴ AB = AE + EB = 8 + 2 = 10 (m),
∴ 学校旗杆的高度为 10 m.
A
B
C
D
相似三角形应用举例:
建筑物高度的测量:
河流宽度的测量:
有遮挡物的问题
表达式:物1高 :物2高 = 影1长 :影2长
第二十七章 相似
27.2 相似三角形
27.2.3 相似三角形应用举例
主讲人:数学可以很简单
1. 能够利用相似三角形的知识,求出不能直接测量
的物体的高度和宽度. (重点)
2. 进一步了解数学建模思想,能够将实际问题转化
为相似三角形的数学模型,提高分析问题、解决
问题的能力. (难点)
上海中心大厦
四川乐山大佛
黄河
今天我们就来学习利用相似三角形可以解决一些不能直接测量的物体的高度及两物之间的距离问题.
知识点1 建筑物高度测量
例1 据传说,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.
如图,木杆 EF 长 2 m,它的影长 FD 为3m,测得 OA 为 201 m,求金字塔的高度 BO.
解:太阳光是平行的光线,因此 ∠BAO =∠EDF.
又 ∠AOB =∠DFE = 90°,∴△ABO ∽△DEF.
∴ ,
∴
=134 (m).
因此金字塔的高度为
134 m.
表达式:物1高 :物2高 = 影1长 :影2长
测量不能到达顶部的物体的高度,可以用“在同一时刻物高与影长成正比例”的原理解决.
方法总结:
小明身高 1.5 米,在操场的影长为 2 米,同时测得教学大楼在操场的影长为 60 米,则教学大楼的高度应为 ( )
A. 45米 B. 40米 C. 90米 D. 80米
A
知识点2 河流宽度的测量
例2 如图,为了估算河的宽度,我们可以在河对岸选定一个目标点 P,在近岸取点 Q 和 S,使点 P,Q,S 共线且直线 PS 与河垂直,接着在过点 S 且与 PS 垂直的直线 a 上选择适当的点 T,确定 PT 与过点 Q 且垂直 PS 的直线 b 的交点 R。已测得 QS = 45 m,ST = 90 m,QR = 60 m,请根据这些数据,计算河宽 PQ。
解:∵ ∠PQR=∠PST=90°,∠P=∠P,
∴ △PQR∽△PST. ∴
即 , ,
PQ×90=(PQ+45)×60.
解得 PQ=90(m).
因此,河宽大约为 90 m.
测量如河宽等不易直接测量的物体的宽度,常构造相似三角形求解.
方法总结:
如图,为了测量水塘边 A、B 两点之间的距离,在可以看到 A、B 的点 E 处,取 AE、BE 延长线上的 C、D 两点,使得 CD∥AB. 若测得 CD=5 m,AD=15m,ED=3 m,则 A、B 两点间的距离为 m.
A
B
E
D
C
20
知识点3 有遮挡物问题
例3 如图,左、右并排的两棵大树的高分别是 AB = 8 m 和 CD = 12 m,两树底部的距离 BD = 5 m,一个人估计自己眼睛距离地面 1.6 m,她沿着正对这两棵树的一条水平直路 l 从左向右前进,当她与左边较低的树的距离小于多少时,就看不到右边较高的树的顶端C 了
分析:如图,设观察者眼睛的位置 (视点) 为点 F,画出观察者的水平视线 FG,它交 AB,CD 于点 H,K.视线 FA,FG 的夹角 ∠AFH 是观察点 A 的仰角. 类似地,∠CFK 是观察点 C 时的仰角,由于树的遮挡,区域Ⅰ和Ⅱ都在观察者看不到的区域 (盲区) 之内. 再往前走就根本看不到 C 点了.
由此可知,如果观察者继续前进,当她与左边的树的距离小于 8 m 时,由于这棵树的遮挡,就看不到右边树的顶端 C .
解:如图,假设观察者从左向右走到点 E 时,她的眼
睛的位置点 E 与两棵树的顶端点 A,C 恰在一条
直线上.
∵AB⊥l,CD⊥l,∴AB∥CD.
∴△AEH∽△CEK.
即
解得:EH=8(m)
已知零件的外径为25 cm,要求它的厚度x,需先求出它的内孔直径AB,现用一个交叉卡钳(AC和BD的长相等)去量(如图),若OA∶OC=OB∶OD=3,CD=7 cm.
求此零件的厚度.
解:∵ ,
而∠AOB=∠COD,
∴△AOB∽△COD.
∴
又∵CD=7 cm,∴AB=21 cm.
由题意和图易知 25-2x=21,∴x=2(cm).
∴此零件的厚度为2 cm.
练习1 在某一时刻,测得一根长为1.8 m的竹竿的影长为3 m,同时测得一栋高楼的影长为90 m,这栋高楼的高度为多少?
x = 54m
解:设这栋高楼的高度为x.
练习2 如图,测得BD=120 m,DC=60 m,EC=50 m,求河宽AB。
解:∵∠ABD=∠ECD=90°,∠ADB=∠EDC,
∴△ABD∽△ECD.
∴
即. 解得AB=100(m)
练习3 如图,某一时刻,旗杆 AB 的影子的一部分在地面上,另一部分在建筑物的墙面上.小明测得旗杆AB 在地面上的影长 BC 为 9.6 m,在墙面上的影长 CD 为 2 m.同一时刻,小明又测得竖立于地面长 1 m 的标杆的影长为 1.2 m.请帮助小明求出旗杆的高度.
A
B
C
D
解:如图:过点 D 作 DE∥BC,交 AB 于点 E,
∴ DE = CB = 9.6 m,BE = CD = 2 m,
∵ 在同一时刻物高与影长成正比例,
∴ EA : ED=1 : 1.2,
∴ AE = 8 m,
∴ AB = AE + EB = 8 + 2 = 10 (m),
∴ 学校旗杆的高度为 10 m.
A
B
C
D
相似三角形应用举例:
建筑物高度的测量:
河流宽度的测量:
有遮挡物的问题
表达式:物1高 :物2高 = 影1长 :影2长
