平面向量的数量积[下学期]
图片预览




文档简介
课件16张PPT。鄞州中学 孙安娜
平面向量的数量积导入新课其中力F 和位移s 是向量, 是F 与s 的夹角,而功是数量.5.6 平面向量的数量积及运算律
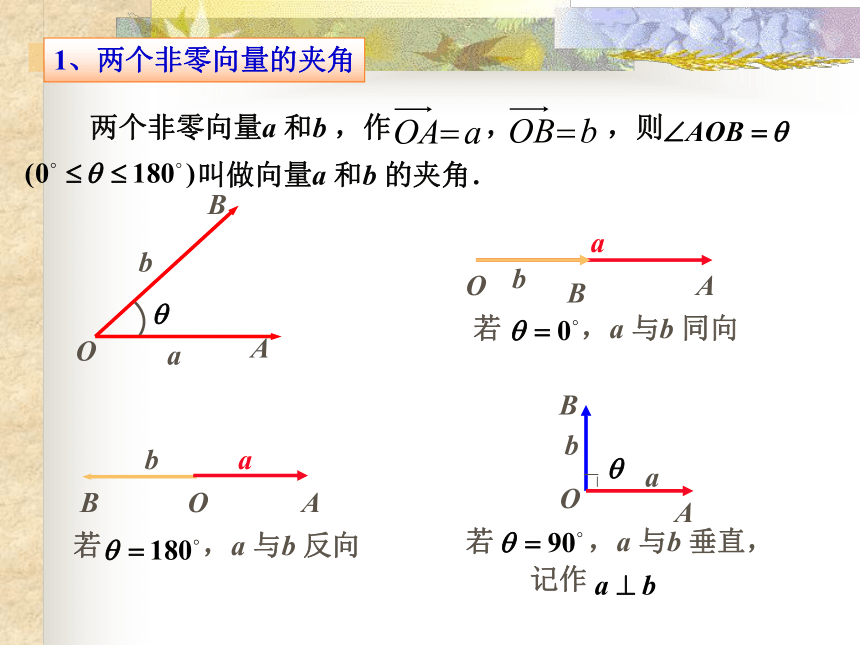
1、两个非零向量的夹角探究:
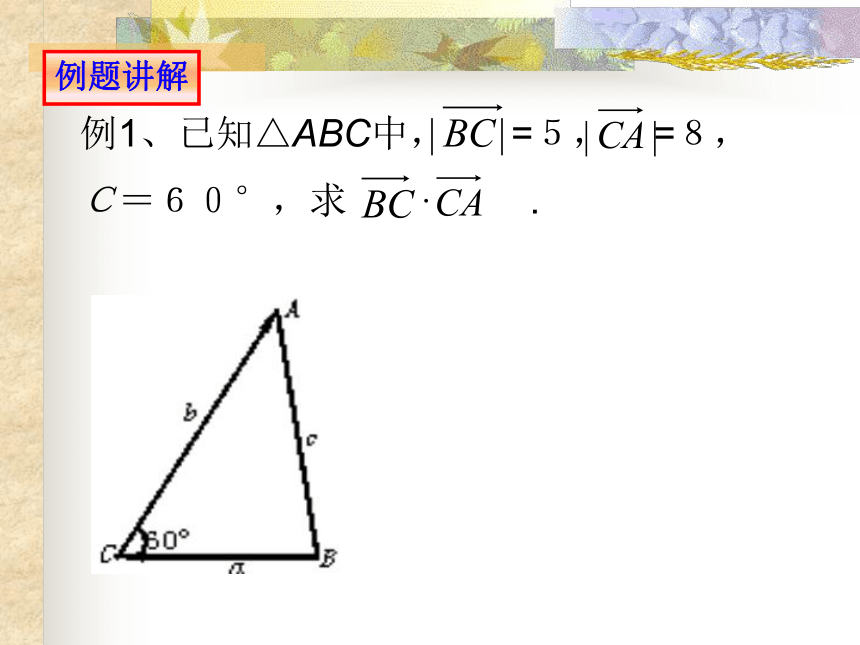
(1)两向量的数量积是一个数量,而不是向量,符号由 夹角决定 (3) a · b不能写成a×b ,a×b 表示向量的另一种运算. (2)一种新的运算法则,以前所学的运算律、性质不适合.例1、已知△ABC中, =5, =8,
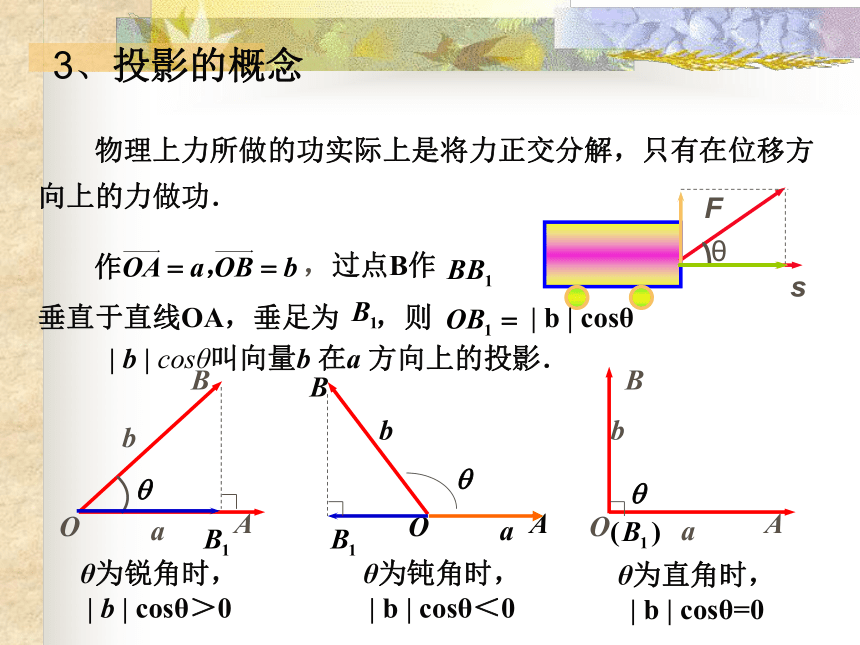
C=60°,求 · .例题讲解| b | cosθ叫向量b 在a 方向上的投影.θ为锐角时,
| b | cosθ>0θ为钝角时,
| b | cosθ<0θ为直角时,
| b | cosθ=03、投影的概念向量的数量积的几何意义:
数量积a?b等于a的长度与b在a方向上投影|b|cos?的乘积。 | b | cosθ叫向量b 在a 方向上的投影.4、向量的数量积的几何意义数量积的重要性质: (1)e · a=a · e=| a | cos? (2)a⊥b a · b=0 (判断两向量垂直的依据) (3)当a 与b 同向时,a · b =| a | · | b |,当a 与b 反向
时, a · b =-| a | · | b | .
特别地(4)(5)a · b ≤| a | · | b |设 都非零向量, 是与 方向相同的单位向量, 是 与 的夹角,则练习:判断下列命题的正误1.若a =0,则对任一向量b ,有a · b=0.2.若a ≠0,则对任一非零向量b ,有a · b≠0.3.若a ≠0,a · b =0,则b=04.若a · b=0,则a · b中至少有一个为0.5.若a≠0,a · b= b · c,则a=c6.对任意向量 a 有例2、已知|a|=4,|b|=5,
(1)当a与b夹角为 时, =——
(2)当a//b时, =——(3)若 则 的夹角为多少?小结:1、两个非零向量的夹角
2、平面向量的数量积的定义
3、投影的概念
4、向量的数量积的几何意义
5、数量积的重要性质
通过本节课学习,要求大家掌握平面向量的数量积定义、几何意义、重要性质,并能运用它们解决相关问题。思考题:
已知 ,且 方向相同,求证
思考题:
已知△ABC中, =5, =8,
C=60°,求 · .二、讲解新课:
平面向量数量积的运算律
1.交换律:a ? b = b ? a
证:设a,b夹角为?,则a ? b = |a||b|cos?,b ? a = |b||a|cos?
∴a ? b = b ? a
2.数乘结合律:(a)?b =(a?b) = a?(b)
证:若> 0,(a)?b =|a||b|cos?, (a?b) =|a||b|cos?,a?(b) =|a||b|cos?,
若< 0,(a)?b =|a||b|cos(???) = ?|a||b|(?cos?) =|a||b|cos?,
(a?b) =|a||b|cos?,
a?(b) =|a||b|cos(???) = ?|a||b|(?cos?) =|a||b|cos?。3.分配律:(a + b)?c = a?c + b?c
在平面内取一点O,作= a, = b,= c,
∵a + b (即)在c方向上的投影等于a、b在c方向上的投影和,
即 |a + b| cos? = |a| cos?1 + |b| cos?2
∴| c | |a + b| cos? =|c| |a| cos?1 + |c| |b| cos?2
∴c?(a + b) = c?a + c?b 即:(a + b)?c = a?c + b?c
说明:(1)一般地,(a·b)с≠a(b·с)
(2)a·с=b·с,с≠0a=b
(3)有如下常用性质:a2=|a|2,
(a+b)(с+d)=a·с+a·d+b·с+b·d
(a+b)2=a2+2a·b+b2再见!再见!再见!
平面向量的数量积导入新课其中力F 和位移s 是向量, 是F 与s 的夹角,而功是数量.5.6 平面向量的数量积及运算律
1、两个非零向量的夹角探究:
(1)两向量的数量积是一个数量,而不是向量,符号由 夹角决定 (3) a · b不能写成a×b ,a×b 表示向量的另一种运算. (2)一种新的运算法则,以前所学的运算律、性质不适合.例1、已知△ABC中, =5, =8,
C=60°,求 · .例题讲解| b | cosθ叫向量b 在a 方向上的投影.θ为锐角时,
| b | cosθ>0θ为钝角时,
| b | cosθ<0θ为直角时,
| b | cosθ=03、投影的概念向量的数量积的几何意义:
数量积a?b等于a的长度与b在a方向上投影|b|cos?的乘积。 | b | cosθ叫向量b 在a 方向上的投影.4、向量的数量积的几何意义数量积的重要性质: (1)e · a=a · e=| a | cos? (2)a⊥b a · b=0 (判断两向量垂直的依据) (3)当a 与b 同向时,a · b =| a | · | b |,当a 与b 反向
时, a · b =-| a | · | b | .
特别地(4)(5)a · b ≤| a | · | b |设 都非零向量, 是与 方向相同的单位向量, 是 与 的夹角,则练习:判断下列命题的正误1.若a =0,则对任一向量b ,有a · b=0.2.若a ≠0,则对任一非零向量b ,有a · b≠0.3.若a ≠0,a · b =0,则b=04.若a · b=0,则a · b中至少有一个为0.5.若a≠0,a · b= b · c,则a=c6.对任意向量 a 有例2、已知|a|=4,|b|=5,
(1)当a与b夹角为 时, =——
(2)当a//b时, =——(3)若 则 的夹角为多少?小结:1、两个非零向量的夹角
2、平面向量的数量积的定义
3、投影的概念
4、向量的数量积的几何意义
5、数量积的重要性质
通过本节课学习,要求大家掌握平面向量的数量积定义、几何意义、重要性质,并能运用它们解决相关问题。思考题:
已知 ,且 方向相同,求证
思考题:
已知△ABC中, =5, =8,
C=60°,求 · .二、讲解新课:
平面向量数量积的运算律
1.交换律:a ? b = b ? a
证:设a,b夹角为?,则a ? b = |a||b|cos?,b ? a = |b||a|cos?
∴a ? b = b ? a
2.数乘结合律:(a)?b =(a?b) = a?(b)
证:若> 0,(a)?b =|a||b|cos?, (a?b) =|a||b|cos?,a?(b) =|a||b|cos?,
若< 0,(a)?b =|a||b|cos(???) = ?|a||b|(?cos?) =|a||b|cos?,
(a?b) =|a||b|cos?,
a?(b) =|a||b|cos(???) = ?|a||b|(?cos?) =|a||b|cos?。3.分配律:(a + b)?c = a?c + b?c
在平面内取一点O,作= a, = b,= c,
∵a + b (即)在c方向上的投影等于a、b在c方向上的投影和,
即 |a + b| cos? = |a| cos?1 + |b| cos?2
∴| c | |a + b| cos? =|c| |a| cos?1 + |c| |b| cos?2
∴c?(a + b) = c?a + c?b 即:(a + b)?c = a?c + b?c
说明:(1)一般地,(a·b)с≠a(b·с)
(2)a·с=b·с,с≠0a=b
(3)有如下常用性质:a2=|a|2,
(a+b)(с+d)=a·с+a·d+b·с+b·d
(a+b)2=a2+2a·b+b2再见!再见!再见!
