任意角的三角函数(张国坤)[下学期]
文档属性
| 名称 | 任意角的三角函数(张国坤)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 404.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-03-13 16:30:00 | ||
图片预览



文档简介
课件31张PPT。任意角的三角函数
(第一课时) 云南省曲靖市第一中学 张国坤教学背景
教学目标
理念方法
教学过程
反馈调节 形象思维抽象思维逻辑思维1.1.1背景-学生基本情况-思维任意角三角函数……
锐角三角函数
函数
角的概念的推广
弧度制
……
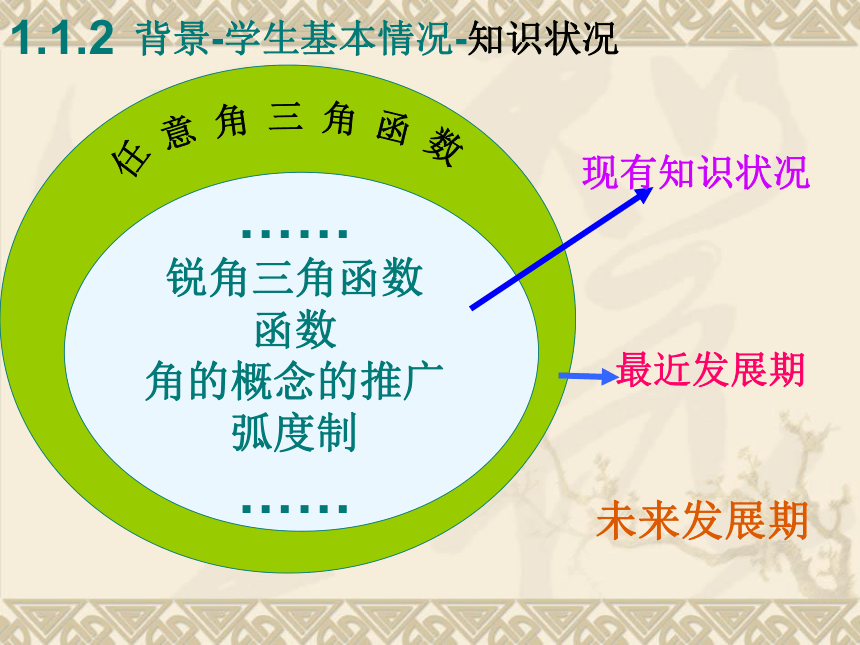
最近发展期现有知识状况未来发展期1.1.2背景-学生基本情况-知识状况
三角函数定义任
意
角三角函数线
定义域
符号
值域
同角关系式
诱导公式变换公式
图象与
性质
反三角
函数斜率
极坐标
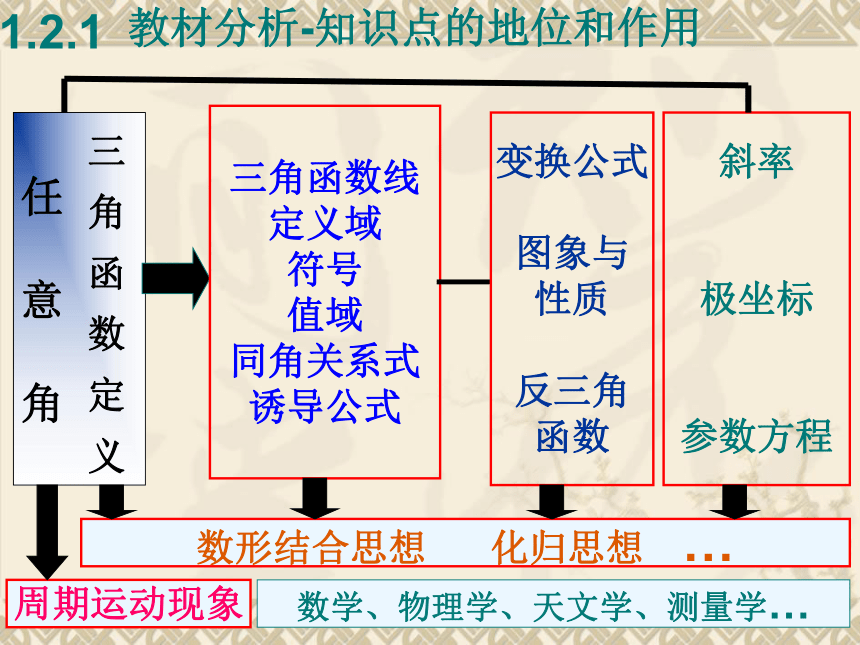
参数方程数形结合思想 化归思想 …周期运动现象数学、物理学、天文学、测量学…1.2.1教材分析-知识点的地位和作用教材分析-重点、难点、关键重点难点关键---坐标为工具,研究正弦
---定义(包括定义域----)理解:三角函数可以看成
是以实数为自变量的函数建立直角坐标系,跳出三
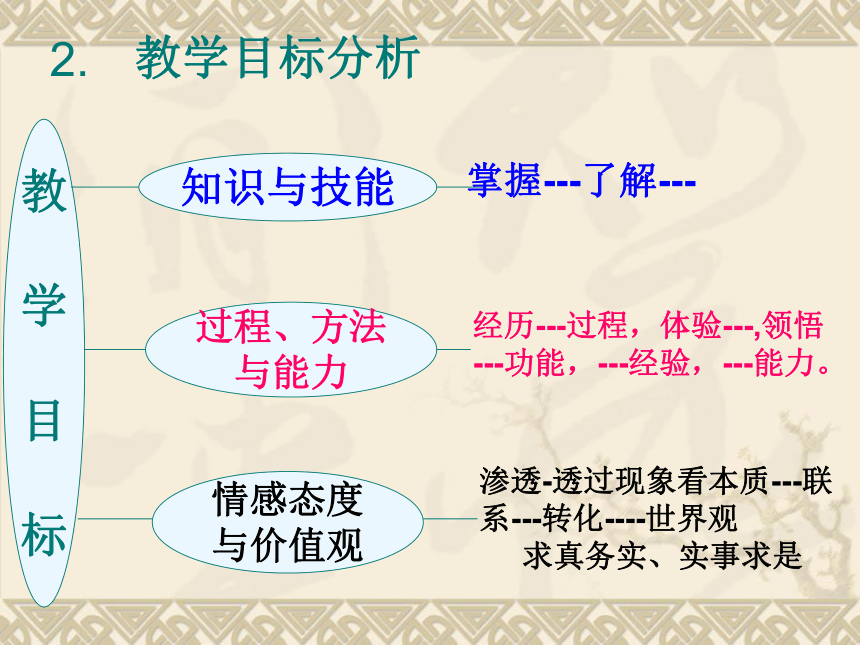
角形限制,化解认知冲突1.2.2教学目标分析教
学
目
标知识与技能过程、方法
与能力情感态度
与价值观掌握---了解---
经历---过程,体验---,领悟
---功能,---经验,---能力。渗透-透过现象看本质---联系---转化----世界观
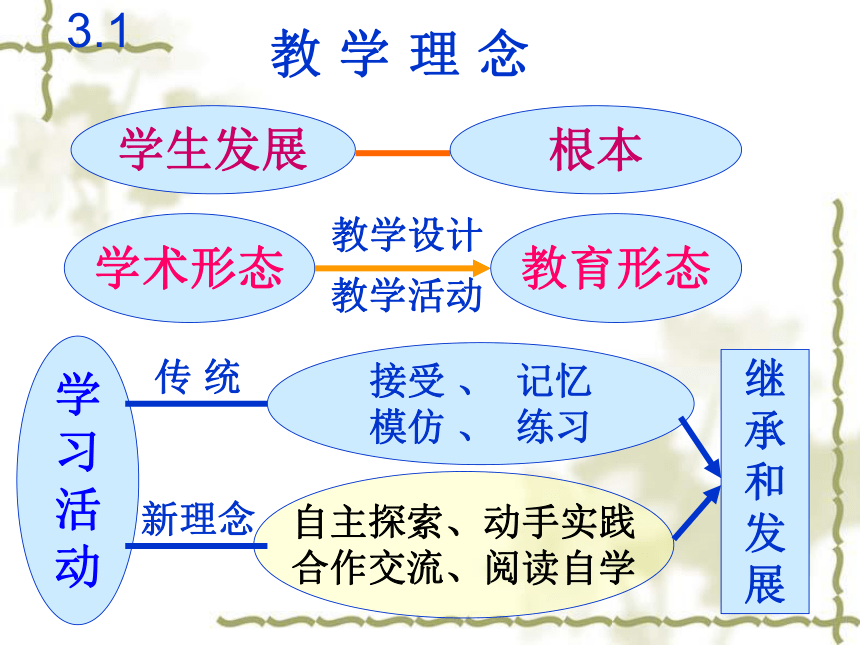
求真务实、实事求是2.学生发展学术形态教学设计学
习
活
动传 统自主探索、动手实践
合作交流、阅读自学接受 、 记忆
模仿 、 练习根本教育形态新理念继
承
和
发
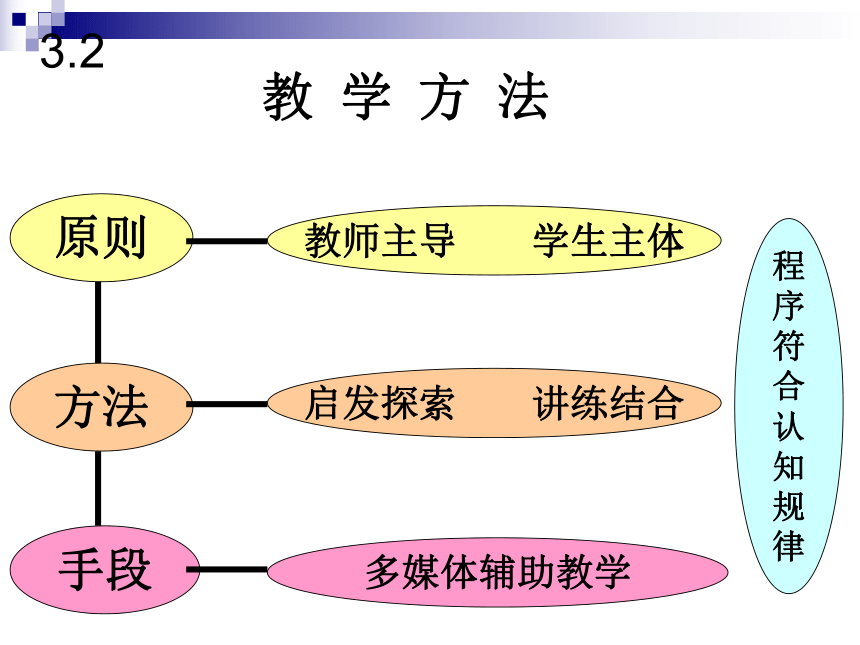
展3.1教学理念教学活动原则方法手段教师主导 学生主体启发探索 讲练结合多媒体辅助教学程
序
符
合
认
知
规
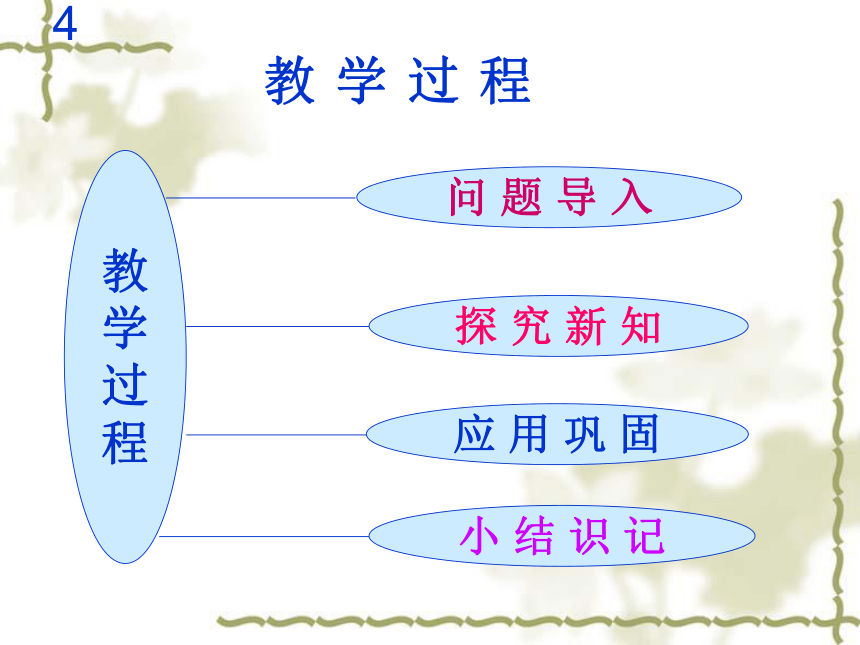
律3.2教学方法教
学
过
程问 题 导 入探 究 新 知应 用 巩 固小 结 识 记4教学过程教学过程--问题导入 1、(请回想)初中对锐角三角函数是怎样规定的? 2、我们已经把锐角推广到了任角,锐角的三角函数概念也能推广到任意角吗?(投影)4.1探
究
新
知探究三角函数定义探究三角函数定义域探究三角函数值符号第一环节第二环节第三环节4.2探究新知 思考题组:
1. 建立恰当的平面直角坐标系,对锐角三角函数
进行再分析? 能跳出三角形的限制吗?
2. 对于第一象限、第二象限、第三象限、第四象
限的角如何呢? 对于90°、180°、270°、
360°的角又如何呢?
3. 对于任意角又如何呢?探究任意角三角函数的定义 4.2.1(投影) 思考题组:
1. 建立恰当的平面直角坐标系,对锐角三角函数
进行再分析? 能跳出三角形的限制吗?
2. 对于第一象限、第二象限、第三象限、第四象
限的角如何呢? 对于90°、180°、270°、
360°的角又如何呢?
3. 对于任意角又如何呢?探究任意角三角函数的定义 4.2.1(投影)= sinα(正弦 )yr= cosα(余弦 )xr=tanα(正切)yx= secα(正割)rx= cscα(余割)ry= cotα(余切)xy 设α是一个任意角,在α终边上除原点外任意取一点P(x,y),P与原点O之间的距离记作r,(形式地)列出六个比值: 归纳得出探索函数内涵 探究:各个比值与角α之间有怎样的 关系?比值是角α的函数吗? (投影) 对于角α的每一个确定值,六个比值(如果存在)都是确定的,不会随P在终边上的移动而变化。
六个比值都随α的变化而变化。
所以,六个比值分别是以角α为自变量、以比值为函数值的函数。 探究成果 三角函数可以看成是
以实数为自变量的函数角的集合与实数集之间
可以建立一一对应关系正弦yr……α……思想性(1)三角形边角关系
锐角三角函数任意角三角函数平面直角坐标系推 广源于三角形又高于三角形特殊一般具体抽象策略性知识思维模式基础迁移创新方法思维内 涵比值与角α之间的对应关系函数知识三角函数知识演绎纳入思想性(2)认知4.2.2探索定义域 问题:三角函数定义中的比值有意义吗?请求出六个三角函数的定义域,填写下表:
引导学生紧扣三角函数定义自主探索
(投影)探索三角函数值的符号4.2.3
引导学生探索
三角函数值的符号取决于x、y值的正负,---- 问题:随着角的终边所在位置的不同,三角函数值的正、负有什么不同?(投影)4.3应用巩固 4.3.1 自学教材例题
例1:已知角α的终边经过点P(2,-3), 求α
的六个三角函数值。
例2:求下列各角的六个三角函数值:
(1) 0;(2)π/2 ;(3) 3π/2。
题1(p19):已知角α的终边经过点P(-3,-1), 求α的
六个三角函数值.
题2(p19题2改编)填表: 4.3.2 课堂练习题1. 已知角α的终边经过点P(x,-3),
cosα=4/5,求α的其它五个三角函数值.
题2. 已知角α的终边在直线y=- x上,求α的六个
三角函数值。4.3.3 变式练习 目的:
巩固和加深对三角函数概念的理解,并训练推理计算技能,培养学生分析问题、解决问题力。
4.4 教学过程--小结识记 根据下列提示归纳识记:
(1)你是怎样把锐角三角函数定义推广到任意角的?或
者说任意角三角函数是怎样定义的?
(2)在三角函数定义中,各比值为什么是角的函数?
(3)你如何判断和记忆正弦、余弦、正切函数的定义域?
(4)你如何记忆正弦、余弦、正切函数值的符号?
(投影)问题形式自主归纳识记人人参与建构知识网络优化知识结构培养认知能力归纳小结搜
集
反
馈
信
息望闻问切察言观色思想情感语言反映思维进程针对性提问引起思考把脉诊断掌握情况了解情况教学反馈5.1教学调节反馈评价及时调控优化过程提高效率5.2
(第一课时) 云南省曲靖市第一中学 张国坤教学背景
教学目标
理念方法
教学过程
反馈调节 形象思维抽象思维逻辑思维1.1.1背景-学生基本情况-思维任意角三角函数……
锐角三角函数
函数
角的概念的推广
弧度制
……
最近发展期现有知识状况未来发展期1.1.2背景-学生基本情况-知识状况
三角函数定义任
意
角三角函数线
定义域
符号
值域
同角关系式
诱导公式变换公式
图象与
性质
反三角
函数斜率
极坐标
参数方程数形结合思想 化归思想 …周期运动现象数学、物理学、天文学、测量学…1.2.1教材分析-知识点的地位和作用教材分析-重点、难点、关键重点难点关键---坐标为工具,研究正弦
---定义(包括定义域----)理解:三角函数可以看成
是以实数为自变量的函数建立直角坐标系,跳出三
角形限制,化解认知冲突1.2.2教学目标分析教
学
目
标知识与技能过程、方法
与能力情感态度
与价值观掌握---了解---
经历---过程,体验---,领悟
---功能,---经验,---能力。渗透-透过现象看本质---联系---转化----世界观
求真务实、实事求是2.学生发展学术形态教学设计学
习
活
动传 统自主探索、动手实践
合作交流、阅读自学接受 、 记忆
模仿 、 练习根本教育形态新理念继
承
和
发
展3.1教学理念教学活动原则方法手段教师主导 学生主体启发探索 讲练结合多媒体辅助教学程
序
符
合
认
知
规
律3.2教学方法教
学
过
程问 题 导 入探 究 新 知应 用 巩 固小 结 识 记4教学过程教学过程--问题导入 1、(请回想)初中对锐角三角函数是怎样规定的? 2、我们已经把锐角推广到了任角,锐角的三角函数概念也能推广到任意角吗?(投影)4.1探
究
新
知探究三角函数定义探究三角函数定义域探究三角函数值符号第一环节第二环节第三环节4.2探究新知 思考题组:
1. 建立恰当的平面直角坐标系,对锐角三角函数
进行再分析? 能跳出三角形的限制吗?
2. 对于第一象限、第二象限、第三象限、第四象
限的角如何呢? 对于90°、180°、270°、
360°的角又如何呢?
3. 对于任意角又如何呢?探究任意角三角函数的定义 4.2.1(投影) 思考题组:
1. 建立恰当的平面直角坐标系,对锐角三角函数
进行再分析? 能跳出三角形的限制吗?
2. 对于第一象限、第二象限、第三象限、第四象
限的角如何呢? 对于90°、180°、270°、
360°的角又如何呢?
3. 对于任意角又如何呢?探究任意角三角函数的定义 4.2.1(投影)= sinα(正弦 )yr= cosα(余弦 )xr=tanα(正切)yx= secα(正割)rx= cscα(余割)ry= cotα(余切)xy 设α是一个任意角,在α终边上除原点外任意取一点P(x,y),P与原点O之间的距离记作r,(形式地)列出六个比值: 归纳得出探索函数内涵 探究:各个比值与角α之间有怎样的 关系?比值是角α的函数吗? (投影) 对于角α的每一个确定值,六个比值(如果存在)都是确定的,不会随P在终边上的移动而变化。
六个比值都随α的变化而变化。
所以,六个比值分别是以角α为自变量、以比值为函数值的函数。 探究成果 三角函数可以看成是
以实数为自变量的函数角的集合与实数集之间
可以建立一一对应关系正弦yr……α……思想性(1)三角形边角关系
锐角三角函数任意角三角函数平面直角坐标系推 广源于三角形又高于三角形特殊一般具体抽象策略性知识思维模式基础迁移创新方法思维内 涵比值与角α之间的对应关系函数知识三角函数知识演绎纳入思想性(2)认知4.2.2探索定义域 问题:三角函数定义中的比值有意义吗?请求出六个三角函数的定义域,填写下表:
引导学生紧扣三角函数定义自主探索
(投影)探索三角函数值的符号4.2.3
引导学生探索
三角函数值的符号取决于x、y值的正负,---- 问题:随着角的终边所在位置的不同,三角函数值的正、负有什么不同?(投影)4.3应用巩固 4.3.1 自学教材例题
例1:已知角α的终边经过点P(2,-3), 求α
的六个三角函数值。
例2:求下列各角的六个三角函数值:
(1) 0;(2)π/2 ;(3) 3π/2。
题1(p19):已知角α的终边经过点P(-3,-1), 求α的
六个三角函数值.
题2(p19题2改编)填表: 4.3.2 课堂练习题1. 已知角α的终边经过点P(x,-3),
cosα=4/5,求α的其它五个三角函数值.
题2. 已知角α的终边在直线y=- x上,求α的六个
三角函数值。4.3.3 变式练习 目的:
巩固和加深对三角函数概念的理解,并训练推理计算技能,培养学生分析问题、解决问题力。
4.4 教学过程--小结识记 根据下列提示归纳识记:
(1)你是怎样把锐角三角函数定义推广到任意角的?或
者说任意角三角函数是怎样定义的?
(2)在三角函数定义中,各比值为什么是角的函数?
(3)你如何判断和记忆正弦、余弦、正切函数的定义域?
(4)你如何记忆正弦、余弦、正切函数值的符号?
(投影)问题形式自主归纳识记人人参与建构知识网络优化知识结构培养认知能力归纳小结搜
集
反
馈
信
息望闻问切察言观色思想情感语言反映思维进程针对性提问引起思考把脉诊断掌握情况了解情况教学反馈5.1教学调节反馈评价及时调控优化过程提高效率5.2
