《乘法分配律》(课件)四年级下册数学苏教版(共12张PPT)
文档属性
| 名称 | 《乘法分配律》(课件)四年级下册数学苏教版(共12张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-10 00:00:00 | ||
图片预览





文档简介
(共12张PPT)
乘法分配律
课前准备
我们已经学习了哪些乘法运算律?这些运算律用字母怎么表示?
乘法交换律:
a×b = b×a
乘法结合律:
(a×b)×c = a×(b×c)
复习巩固
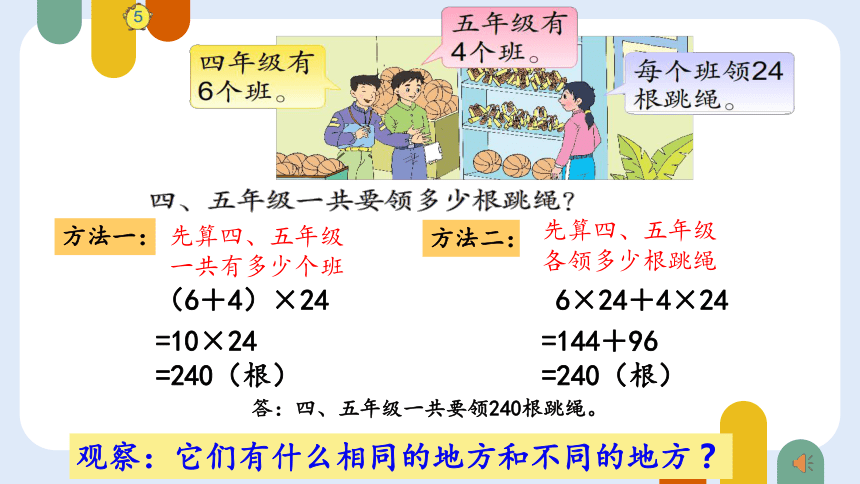
6×24+4×24
=144+96
=240(根)
(6+4)×24
=10×24
=240(根)
方法一:
先算四、五年级一共有多少个班
先算四、五年级各领多少根跳绳
方法二:
观察:它们有什么相同的地方和不同的地方?
答:四、五年级一共要领240根跳绳。
10个24
6个24+4个24,也是10个24
(6+4)×24
6×24+4×24
=
探索新知
为什么两个算式的结构不同,
结果竟然是相等的呢?
(30+15)×2 =
分别去乘2
(5+10)×8 = 5×8 + 10×8
5个8+10个8=15个8
(16+27)×3 = 16×3 + 27×3
16个3+27个3=43个3
(4+9)×18 = 4×18 + 9×18
4个18+9个18=13个18
探索新知
+
30×2
15×2
15个8
同学们你还能写几个这样的等式吗?
43个3
13个18
这些等式,都是把括号里的数字分别去乘括号外面的数字,我 们简称它是从合到分。
试一试
64×9+36×9 =
(64+36)×9
把它们的个数合并起来,放进括号里,就是64+36,然后再×9,一共是100个9
(a + b)× c = a × c + b × c
两个数的和与一个数相乘,可以先把这两个数分别与这个数相乘,再相加。这就是
乘法分配律。
64个9 + 36个9
你能用三个不同的字母,比如用a,b,c写一个等式,表示出上面这些等式所反映的规律吗?
第1题:在□里填数,在○里填运算符号。
①(42+35)×2 = 42× +35×
② 27×12+43×12 =(27+ )×
③ 15×26+15×14 = ( )
④ 72×(30+6)=
2
2
43
12
15
×
+
26
14
72
30
+
6
72
×
×
从合到分
从分到合
练一练
30 × 72 + 6 × 72
观察:你发现哪些等式结构相同?
第2题:横着看,在得数相同的算式后面画“√”。
(28+16)× 7 28×7+16×7
15×39+45×39 (15+45)× 39
74 ×(20+1) 74×20+74
40×50+50×90 40 ×(50+90)
√
√
√
×1
练一练
50 ×(40+90) √
(40+90)× 50 √
(64+26)×2
=90×2
=180(米)
64×2+26×2
64×2+26×2
=128+52
=180(米)
=
第3题:用两种不同的方法计算长方形菜地(如右图)的周长,并说说它们之间的联系。
(64+26)×2
练一练
方法一:
方法二:
答:长方形菜地的周长是180米。
两个数的和与一个数相乘,可以先把这两个数分别与这个数相乘,再相加,这就是乘法分配律。
用字母可以表示为:(a+b)× c = a×c + b×c
回顾总结
谢 谢 聆 听
乘法分配律
课前准备
我们已经学习了哪些乘法运算律?这些运算律用字母怎么表示?
乘法交换律:
a×b = b×a
乘法结合律:
(a×b)×c = a×(b×c)
复习巩固
6×24+4×24
=144+96
=240(根)
(6+4)×24
=10×24
=240(根)
方法一:
先算四、五年级一共有多少个班
先算四、五年级各领多少根跳绳
方法二:
观察:它们有什么相同的地方和不同的地方?
答:四、五年级一共要领240根跳绳。
10个24
6个24+4个24,也是10个24
(6+4)×24
6×24+4×24
=
探索新知
为什么两个算式的结构不同,
结果竟然是相等的呢?
(30+15)×2 =
分别去乘2
(5+10)×8 = 5×8 + 10×8
5个8+10个8=15个8
(16+27)×3 = 16×3 + 27×3
16个3+27个3=43个3
(4+9)×18 = 4×18 + 9×18
4个18+9个18=13个18
探索新知
+
30×2
15×2
15个8
同学们你还能写几个这样的等式吗?
43个3
13个18
这些等式,都是把括号里的数字分别去乘括号外面的数字,我 们简称它是从合到分。
试一试
64×9+36×9 =
(64+36)×9
把它们的个数合并起来,放进括号里,就是64+36,然后再×9,一共是100个9
(a + b)× c = a × c + b × c
两个数的和与一个数相乘,可以先把这两个数分别与这个数相乘,再相加。这就是
乘法分配律。
64个9 + 36个9
你能用三个不同的字母,比如用a,b,c写一个等式,表示出上面这些等式所反映的规律吗?
第1题:在□里填数,在○里填运算符号。
①(42+35)×2 = 42× +35×
② 27×12+43×12 =(27+ )×
③ 15×26+15×14 = ( )
④ 72×(30+6)=
2
2
43
12
15
×
+
26
14
72
30
+
6
72
×
×
从合到分
从分到合
练一练
30 × 72 + 6 × 72
观察:你发现哪些等式结构相同?
第2题:横着看,在得数相同的算式后面画“√”。
(28+16)× 7 28×7+16×7
15×39+45×39 (15+45)× 39
74 ×(20+1) 74×20+74
40×50+50×90 40 ×(50+90)
√
√
√
×1
练一练
50 ×(40+90) √
(40+90)× 50 √
(64+26)×2
=90×2
=180(米)
64×2+26×2
64×2+26×2
=128+52
=180(米)
=
第3题:用两种不同的方法计算长方形菜地(如右图)的周长,并说说它们之间的联系。
(64+26)×2
练一练
方法一:
方法二:
答:长方形菜地的周长是180米。
两个数的和与一个数相乘,可以先把这两个数分别与这个数相乘,再相加,这就是乘法分配律。
用字母可以表示为:(a+b)× c = a×c + b×c
回顾总结
谢 谢 聆 听
