正弦函数的性质和图象2[下学期]
图片预览




文档简介
课件16张PPT。丽水市职业高级中学欢迎您
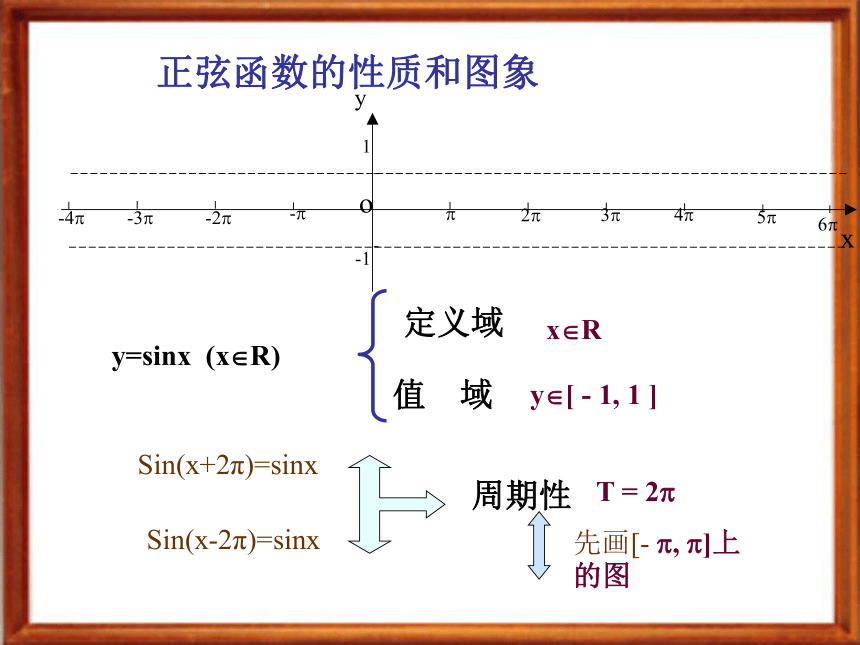
正弦函数的性质与图象(一)执教者:李勇伟(一)创设情境(二)探索研究 正弦函数的性质和图象y=sinx (x?R) 定义域值 域周期性x?Ry?[ - 1, 1 ]T = 2?Sin(x+2π)=sinxSin(x-2π)=sinx先画[- ?, ?]上的图 sin(-x)= - sinx (x?R) y=sinx (x?R)是奇函数
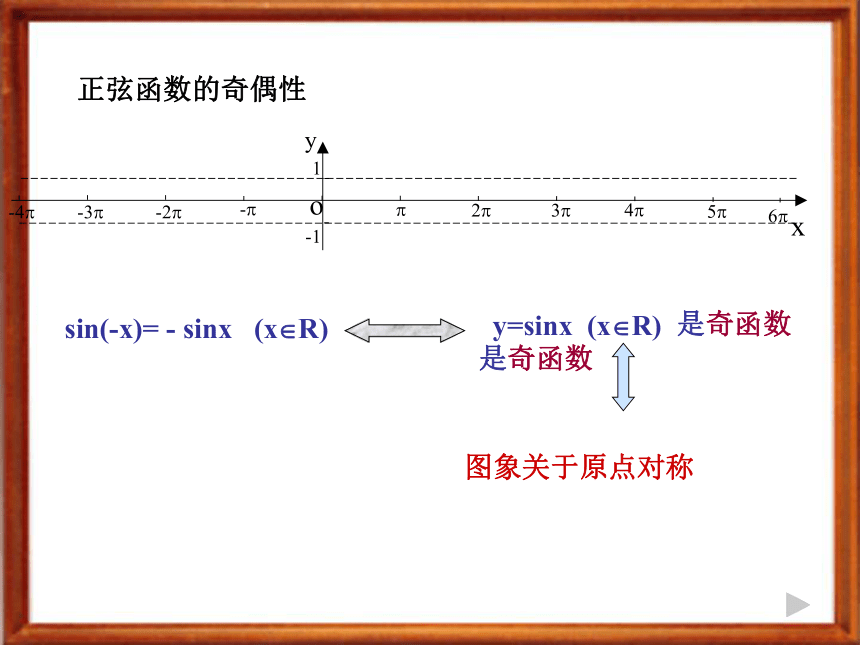
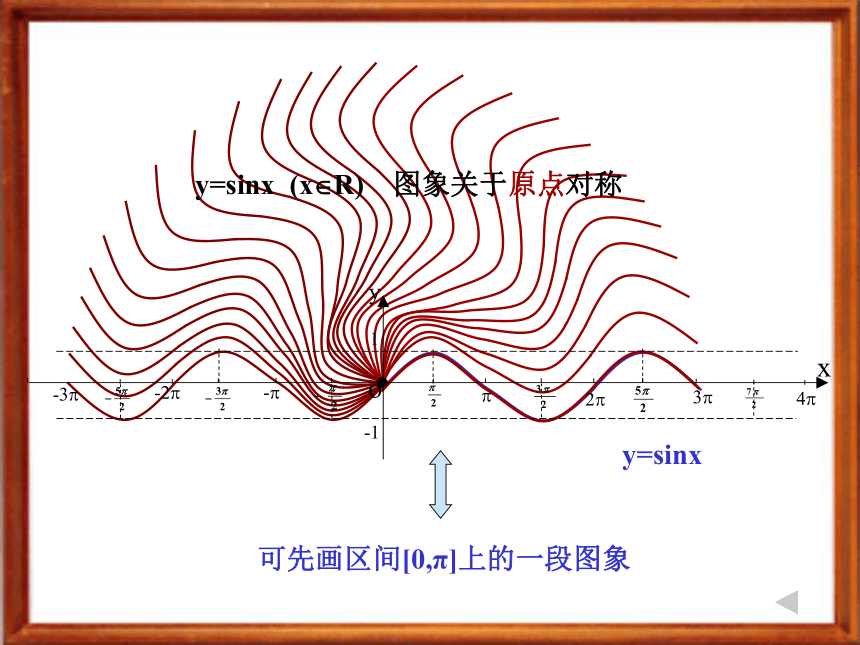
是奇函数图象关于原点对称 正弦函数的奇偶性 y=sinxy=sinx (x?R) 图象关于原点对称可先画区间[0,π]上的一段图象 正弦函数的单调性 y=sinx (x?R)增区间为 [ , ] 其值从-1增至1 … 0 … … ? …-1 0 1 0 -1减区间为 [ , ] 其值从 1减至-1[ +2k?, +2k?],k?Z[ +2k?, +2k?],k?Z问题:该单调性表明图象在区间 [0,π]上有什么特征呢?在图象上表现为:在[0, π/2]上图象是逐渐上升,在[π/2, π]上是逐渐下降.想一想:综合以上函数性质的研究,你觉得该如何画正弦函数的图象?[看一看,想一想:]请你仔细观察刚才所画的正弦函数图象,试想:如果只要求大致画出f(x)=sinx在[0,2 π]上的一段图象,你能想出一种更简单的画法吗?3.总结归纳“五点法”如果只要求大致画出在上的一段图象,那么我们可以只要描出5个特殊点:
(0,0),(π/2,1),(π,0),(3π/2,-1), (2 π,0)
然后,把它们用一条先单调上升,接着单调下降,最后又单调上升且连续不断的曲线连接起来.习惯上称这种方法为“五点法”4.反馈演练用“五点法”作出f(x)=sinx在x∈[0,2 π]上的简图.5.拓展 例1 不通过求值,指出下列各式大于0还是小于0:
(1) sin( ) – sin( )(2) cos( ) - cos( ) 解:?又 y=sinx 在 上是增函数解:?又 y=cosx 在 上是减函数cos( )=cos =cos cos( )=cos =cos 从而 cos( ) - cos( ) <0 例2 求下列函数的单调区间: (1) y=2sin(-x )解: y=2sin(-x )= -2sinx (2) y=3sin(2x- ) 单调增区间为所以:解:单调减区间为小 结: 正弦函数的性质和图象 奇偶性 单调性(单调区间)奇函数[ +2k?, +2k?],k?Z单调递增[ +2k?, +2k?],k?Z单调递减函数
正弦函数的性质与图象(一)执教者:李勇伟(一)创设情境(二)探索研究 正弦函数的性质和图象y=sinx (x?R) 定义域值 域周期性x?Ry?[ - 1, 1 ]T = 2?Sin(x+2π)=sinxSin(x-2π)=sinx先画[- ?, ?]上的图 sin(-x)= - sinx (x?R) y=sinx (x?R)是奇函数
是奇函数图象关于原点对称 正弦函数的奇偶性 y=sinxy=sinx (x?R) 图象关于原点对称可先画区间[0,π]上的一段图象 正弦函数的单调性 y=sinx (x?R)增区间为 [ , ] 其值从-1增至1 … 0 … … ? …-1 0 1 0 -1减区间为 [ , ] 其值从 1减至-1[ +2k?, +2k?],k?Z[ +2k?, +2k?],k?Z问题:该单调性表明图象在区间 [0,π]上有什么特征呢?在图象上表现为:在[0, π/2]上图象是逐渐上升,在[π/2, π]上是逐渐下降.想一想:综合以上函数性质的研究,你觉得该如何画正弦函数的图象?[看一看,想一想:]请你仔细观察刚才所画的正弦函数图象,试想:如果只要求大致画出f(x)=sinx在[0,2 π]上的一段图象,你能想出一种更简单的画法吗?3.总结归纳“五点法”如果只要求大致画出在上的一段图象,那么我们可以只要描出5个特殊点:
(0,0),(π/2,1),(π,0),(3π/2,-1), (2 π,0)
然后,把它们用一条先单调上升,接着单调下降,最后又单调上升且连续不断的曲线连接起来.习惯上称这种方法为“五点法”4.反馈演练用“五点法”作出f(x)=sinx在x∈[0,2 π]上的简图.5.拓展 例1 不通过求值,指出下列各式大于0还是小于0:
(1) sin( ) – sin( )(2) cos( ) - cos( ) 解:?又 y=sinx 在 上是增函数解:?又 y=cosx 在 上是减函数cos( )=cos =cos cos( )=cos =cos 从而 cos( ) - cos( ) <0 例2 求下列函数的单调区间: (1) y=2sin(-x )解: y=2sin(-x )= -2sinx (2) y=3sin(2x- ) 单调增区间为所以:解:单调减区间为小 结: 正弦函数的性质和图象 奇偶性 单调性(单调区间)奇函数[ +2k?, +2k?],k?Z单调递增[ +2k?, +2k?],k?Z单调递减函数
