余弦定理1[下学期]

课件14张PPT。余弦定理 正弦定理 在一个三角形中，各边和　它所对角的正弦值的比相等，即正弦定理可以解哪几类的三角形问题？ （1）已知两角和任一边，求其他两边和一角；（2）已知两边和其中一边的对角，求另一边的对角（进而求出其他的边和角）。什么叫正弦定理 ？ 因为某种实际需要，需测量左图中A、B二点间的距离。如何测量？ 实际测量中，测量人员在如图所示位置取点C，用皮尺测得AC=8米，BC=5米，∠ACB= 。由此测量人员可以得到AB的长度。
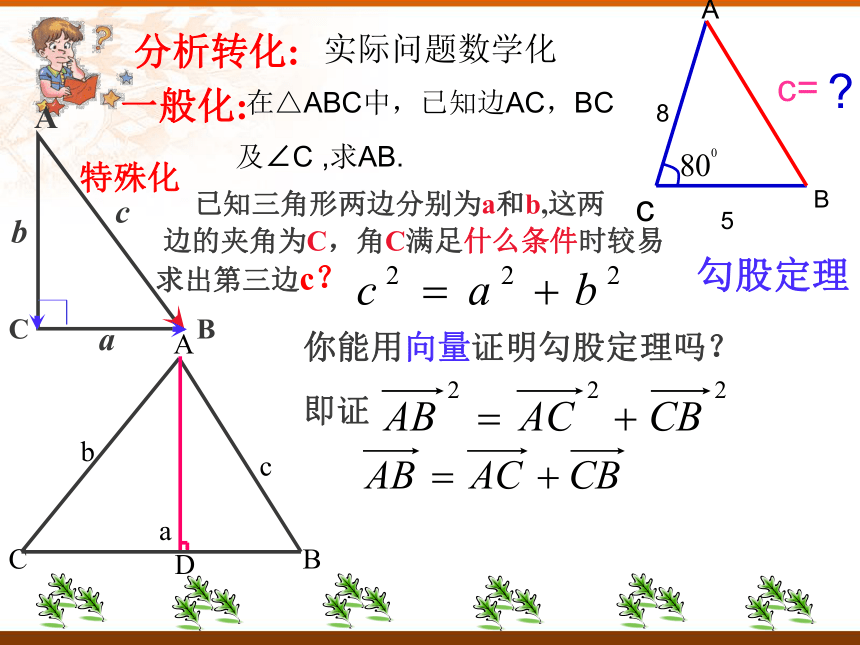
问：怎么样算AB的长度？实际问题数学化 在△ABC中，已知边AC，BC
及∠C ,求AB.分析转化:一般化: 已知三角形两边分别为a和b,这两
边的夹角为C，角C满足什么条件时较易
求出第三边c？勾股定理你能用向量证明勾股定理吗？即证特殊化 余弦定理 a2=b2+c2-2bc·cosA
b2=c2+a2-2ca·cosB
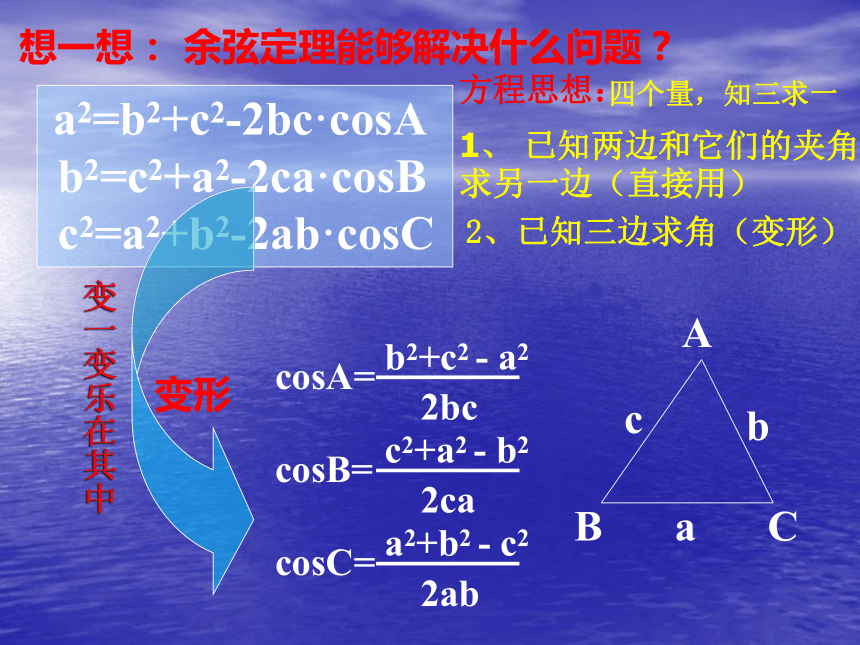
c2=a2+b2-2ab·cosC你能用文字说明吗？ 三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。 想一想： 余弦定理能够解决什么问题？ a2=b2+c2-2bc·cosA
b2=c2+a2-2ca·cosB
c2=a2+b2-2ab·cosC方程思想：四个量，知三求一1、 已知两边和它们的夹角求另一边（直接用）2、已知三边求角（变形）练一练：会用才是硬道理 1、在△ABC中，已知a= , c=2 ，B=150。，求b。 2、已知△ABC的三边为 、2、1，求它的最大内角。解：
例1、在三角形ABC中，已知a=7, b=10, c=6,求A，B，C（精确到 ）思考：已知条件不变，将例1稍做改动
（1）在三角形ABC中，已知a=7,b=10,c=6,判定三角形ABC的形状变式1:已知三角形三边长为a,b,c,怎样判断△ABC是锐角三角形,直角三角形还是钝角三角形？设a是最长边,则
△ABC是直角三角形?a2=b2+c2
△ABC是锐角三角形?a2 △ABC是钝角三角形?a2>b2+c2例3：在三角形ABC中，已知a=7,b=8,cosC= ,求最大角的余弦值分析：求最大角的余弦值，最主要的是判断哪个角是最大角。由大边对大角，已知两边可求出第三边,找到最大角。解：则有：b是最大边，那么B 是最大角例4：一钝角三角形的边长为连续自然数，则这三边长为（ ）
A、1，2，3 B、2，3，4 C、3，4，5 D、4，5，6分析： 要看哪一组符合要求，只需检验哪一个选项
中的最大角是钝角，即该角的余弦值小于0。B中： ，所以C是钝角D中： ，所以C是锐角，
因此以4，5，6为三边长的三角形是锐角三角形A、C显然不满足B总结（1）余弦定理适用于任何三角形（3）由余弦定理可知：（2）余弦定理的作用： a、已知三边，求三个角 b、已知两边及这两边的夹角，求第三边，进而可求出其它两个角c、判断三角形的形状