14.1.4整式的乘法(2) 课件(共25张PPT)
文档属性
| 名称 | 14.1.4整式的乘法(2) 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 943.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-10 17:55:08 | ||
图片预览






文档简介
(共25张PPT)
人教版 八年级上册
14.1.4 整式的乘法(2)
课件说明
学习目标:
1.理解单项式与多项式相乘的法则,能运用单项式
与多项式相乘的法则进行计算.
2.理解算理,发展学生的运算能力和“几何直观”
观念,体会转化、数形结合和程序化思想.
学习重点:单项式与多项式相乘的法则的运用.
单项式乘以单项式的法则:
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
复习旧知
1.计算 3ab ·5a b 的结果是( ).
A.8a b B. 8a b C. 15a b D. 15a b
2.化简(-3x )·2x 的结果是 ( ).
A. -6x5 B. -3x5 C.5x5 D. 6x6
C
A
3.计算:
(1)2a·a = ;
(2)4x2·(-2xy)= ;
(3)3m · (-2mn ) = .
2a
-8x3y
12m4n4
4.若一个三角形的底边长为 4a,底边上的
高为2h,则它的面积为 .
4ah
你在计算这3 个小题时,分别用到了学过的哪些知识、法则或运算律?
(1) 4xy
3x2y
●
=
12x3y2
=
a3b2
1
4
=
(3)
(-12)
×
( + - )
1
6
1
4
1
3
(-12)
×
1
3
(-12)
×
1
4
(-12)
×
1
6
-
+
(-3 )
=
-4
-
(-2)
=
-5.
+
探究新知
( - ab2 )
(2)(-2a2 )
1
8
●
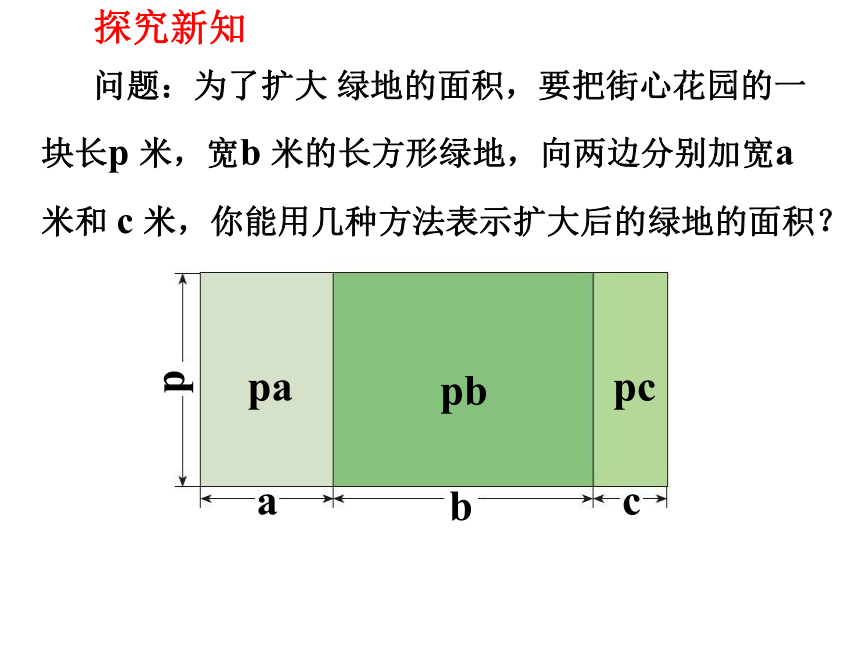
问题:为了扩大 绿地的面积,要把街心花园的一块长p 米,宽b 米的长方形绿地,向两边分别加宽a 米和 c 米,你能用几种方法表示扩大后的绿地的面积?
a
b
c
pa
pb
pc
p
探究新知
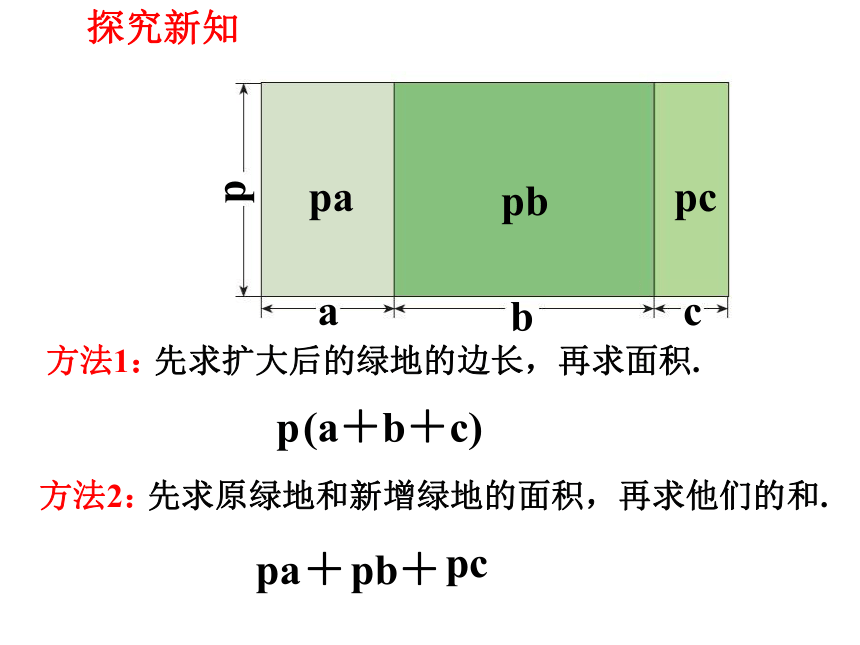
方法1:
a
b
c
pa
pb
pc
p
先求扩大后的绿地的边长,再求面积.
方法2:
先求原绿地和新增绿地的面积,再求他们的和.
(a+b+c)
p
pb
pa
pc
+
+
探究新知
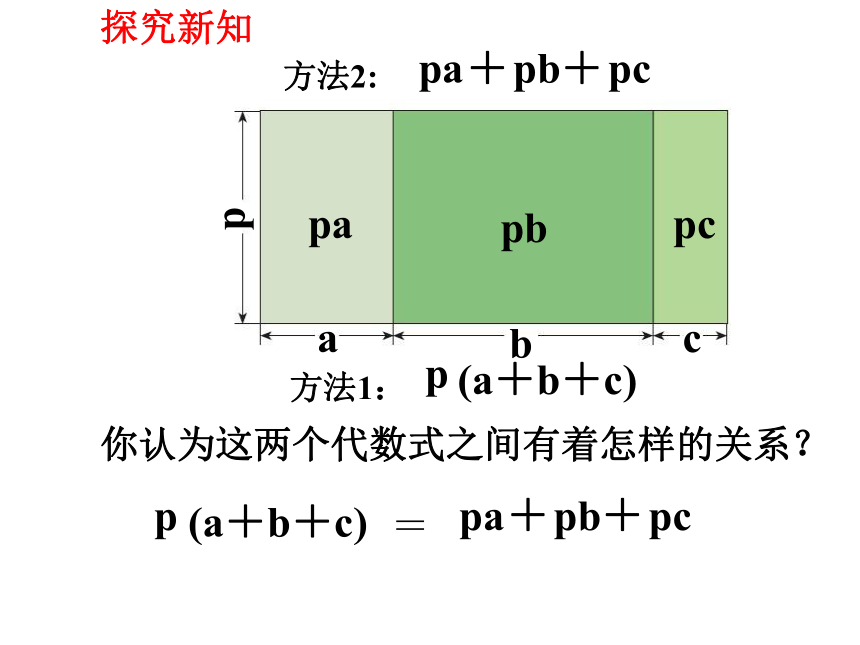
你认为这两个代数式之间有着怎样的关系?
方法1:
a
b
c
pa
pb
pc
p
方法2:
(a+b+c)
p
pb
pa
pc
+
+
(a+b+c)
p
pb
pa
pc
+
+
=
探究新知
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
请你用自己的语言概括单项式乘以多项式的法则.
单项式乘以多项式的法则:
pb
pa
pc
+
+
(a+b+c)
p
=
学习新知
下面的计算对不对?如果不对,应该怎样改?
(1) 3( a-1) =3a2
(2) 2x2 (x-y) =2x3-2x2
( )
( )
( )
( )
(3) (-3x2)(x-y) =-3x3-3x2y
(4) (-5a)(a2-b) =-5a3+5ab
×
×
×
√
练习巩固
(3x)
例5 计算:
(1) (-4x2)(3x+1) ;
●
(2) ( ab2-2ab)
( ab)
1
2
2
3
解:
(1) (-4x2)(3x+1)
=
●
(-4x2)
+
●
(-4x2)
1
=
-12x3
-4x2
( ab)
●
(2) ( ab2-2ab)
1
2
2
3
=
=
( ab2)
2
3
●
( ab)
1
2
+
●
(-2ab)
( ab)
1
2
a2b3
1
3
-a2 b2
例题解析
(1) 3a(5a-2b) ;
(3) 5x(2x2-4x+3) ;
(2) (x-3y) (-6x );
(4) (-2a)(a2-ab+b2) .
1.计算:
练习巩固
=
15a2-6ab;
=
-6x2+18xy ;
=
10x3-20x2+15x ;
-2a3 +2a2b-2ab2.
=
2.化简:
(2) x2(x-1)+2x (x2-2x+3) ;
(3) x ( x+1)
-3x( x-2) .
3
2
1
2
(1) x(x-1)+2x (x+1) -3x(2x-5)
练习巩固
解:
(2) x2(x-1)+2x (x2-2x+3)
(1) x(x-1)+2x (x+1) -3x(2x-5)
=
x2-x
-6x2+15x
+2x2+2x
=
- 3x2+16x
=
=
x3-x2
+2x3 -4x2 +6x
3x3-5x2+6x
=
=
x2+x
- x2+6x
-4x2+7x.
1
2
9
2
(3) x ( x+1)
-3x( x-2)
3
2
1
2
例2 化简:
x(x2-x) +2x2(x+1),
解:
x(x2-x) +2x2(x+1)
=
x3-x2 +2x3+2x2
=
3x3+x2
其中x=-2.
当x =-2 时,
原式=3×(-2)3+(-2)2
=
-20
=
-24
+
4
例题解析
先化简,再求值:
3a(2a2-4a+3)-2a2(3a+4),其中a= -2.
练习巩固
解:原式=
6a3 -12a2+9a
-6a3 - 8a2
=-20a2 +9a.
当a=-2时,
原式=-20×(- 2)2+9×(-2)
= - 98.
=-20×4+(-18)
(1)本节课学习了哪些主要内容?
(2)在运用单项式与多项式相乘的法则时,你认为
应该注意哪些问题?
(3)探索单项式与多项式相乘的法则的过程,体现
了哪些思想方法?
课堂小结
1.计算2x(3x2+1)的结果正确的是( ).
A. 5x3+2x2 B. 6x + 1
C. 6x +2x D. 6x2+2x
2.化简(-3a+ b)·(-7ab2)的结果是( ).
A.21a2b2+14ab3 B.21a2b2- ab3
C.-21a2b2+14ab3 D. -21a2b2+ ab3
7
2
7
2
1
2
C
B
巩固提高
3.计算(-3x)·(2x2-5x-1)的结果是 ( ).
A. -6x2-15x2 - 3x B. -6x3+15x2+3x
C. -6x+15x2 D. -6x3+15x2-1
4.要使x(x+a)+3x-2b=x2+5x+4成立,
则a,b的值分别为 ( ).
A.-2, -2 B.2,2
C.2, -2 D.-2,2
B
C
5.若x3(3xm-2xn+4xk) =3x9-2x6+4x4,则
m,n,k 的值分别为 ( ).
A.6,3,1 B.3,6,1
C.2,1,3 D.2,3,1
A
6.计算:
(1)ab·(a+1)= ;
(2)(-2a)( a3 -1)= ;
(3) -3xy(-3x y +xy) = .
a b+ab
9x3y2-3x2y2
1
4
- a4+2a
1
2
7.已知2m-3n=-5,则代数式m(n-4)-n(m-6)
的值为 .
8.现规定一种运算a*b=ab+a-b,其中a,b为实
数则a*b+(b-a)*b= .
10
b2-b
=ab+a-b
+(b-a)b+(b-a)-b
9.某长方体的长3m-4,宽为2m,高为m,则它
的体积为 .
6m3-8m2
10.某同学在计算一个多项式乘以-3x2时,因抄
错运算符号,算成了加上-3x2,得到的结果
是x2-4x+1,那么正确的计算结果是多少
(x2- 4x+1)-(-3x )
正确的计算结果是
解:这个多项式是
(4x2-4x+1)(-3x2)
=4x2-4x+1
=-12x4+12x3-3x2.
今天作业
课本P105页第4、7题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 八年级上册
14.1.4 整式的乘法(2)
课件说明
学习目标:
1.理解单项式与多项式相乘的法则,能运用单项式
与多项式相乘的法则进行计算.
2.理解算理,发展学生的运算能力和“几何直观”
观念,体会转化、数形结合和程序化思想.
学习重点:单项式与多项式相乘的法则的运用.
单项式乘以单项式的法则:
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
复习旧知
1.计算 3ab ·5a b 的结果是( ).
A.8a b B. 8a b C. 15a b D. 15a b
2.化简(-3x )·2x 的结果是 ( ).
A. -6x5 B. -3x5 C.5x5 D. 6x6
C
A
3.计算:
(1)2a·a = ;
(2)4x2·(-2xy)= ;
(3)3m · (-2mn ) = .
2a
-8x3y
12m4n4
4.若一个三角形的底边长为 4a,底边上的
高为2h,则它的面积为 .
4ah
你在计算这3 个小题时,分别用到了学过的哪些知识、法则或运算律?
(1) 4xy
3x2y
●
=
12x3y2
=
a3b2
1
4
=
(3)
(-12)
×
( + - )
1
6
1
4
1
3
(-12)
×
1
3
(-12)
×
1
4
(-12)
×
1
6
-
+
(-3 )
=
-4
-
(-2)
=
-5.
+
探究新知
( - ab2 )
(2)(-2a2 )
1
8
●
问题:为了扩大 绿地的面积,要把街心花园的一块长p 米,宽b 米的长方形绿地,向两边分别加宽a 米和 c 米,你能用几种方法表示扩大后的绿地的面积?
a
b
c
pa
pb
pc
p
探究新知
方法1:
a
b
c
pa
pb
pc
p
先求扩大后的绿地的边长,再求面积.
方法2:
先求原绿地和新增绿地的面积,再求他们的和.
(a+b+c)
p
pb
pa
pc
+
+
探究新知
你认为这两个代数式之间有着怎样的关系?
方法1:
a
b
c
pa
pb
pc
p
方法2:
(a+b+c)
p
pb
pa
pc
+
+
(a+b+c)
p
pb
pa
pc
+
+
=
探究新知
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
请你用自己的语言概括单项式乘以多项式的法则.
单项式乘以多项式的法则:
pb
pa
pc
+
+
(a+b+c)
p
=
学习新知
下面的计算对不对?如果不对,应该怎样改?
(1) 3( a-1) =3a2
(2) 2x2 (x-y) =2x3-2x2
( )
( )
( )
( )
(3) (-3x2)(x-y) =-3x3-3x2y
(4) (-5a)(a2-b) =-5a3+5ab
×
×
×
√
练习巩固
(3x)
例5 计算:
(1) (-4x2)(3x+1) ;
●
(2) ( ab2-2ab)
( ab)
1
2
2
3
解:
(1) (-4x2)(3x+1)
=
●
(-4x2)
+
●
(-4x2)
1
=
-12x3
-4x2
( ab)
●
(2) ( ab2-2ab)
1
2
2
3
=
=
( ab2)
2
3
●
( ab)
1
2
+
●
(-2ab)
( ab)
1
2
a2b3
1
3
-a2 b2
例题解析
(1) 3a(5a-2b) ;
(3) 5x(2x2-4x+3) ;
(2) (x-3y) (-6x );
(4) (-2a)(a2-ab+b2) .
1.计算:
练习巩固
=
15a2-6ab;
=
-6x2+18xy ;
=
10x3-20x2+15x ;
-2a3 +2a2b-2ab2.
=
2.化简:
(2) x2(x-1)+2x (x2-2x+3) ;
(3) x ( x+1)
-3x( x-2) .
3
2
1
2
(1) x(x-1)+2x (x+1) -3x(2x-5)
练习巩固
解:
(2) x2(x-1)+2x (x2-2x+3)
(1) x(x-1)+2x (x+1) -3x(2x-5)
=
x2-x
-6x2+15x
+2x2+2x
=
- 3x2+16x
=
=
x3-x2
+2x3 -4x2 +6x
3x3-5x2+6x
=
=
x2+x
- x2+6x
-4x2+7x.
1
2
9
2
(3) x ( x+1)
-3x( x-2)
3
2
1
2
例2 化简:
x(x2-x) +2x2(x+1),
解:
x(x2-x) +2x2(x+1)
=
x3-x2 +2x3+2x2
=
3x3+x2
其中x=-2.
当x =-2 时,
原式=3×(-2)3+(-2)2
=
-20
=
-24
+
4
例题解析
先化简,再求值:
3a(2a2-4a+3)-2a2(3a+4),其中a= -2.
练习巩固
解:原式=
6a3 -12a2+9a
-6a3 - 8a2
=-20a2 +9a.
当a=-2时,
原式=-20×(- 2)2+9×(-2)
= - 98.
=-20×4+(-18)
(1)本节课学习了哪些主要内容?
(2)在运用单项式与多项式相乘的法则时,你认为
应该注意哪些问题?
(3)探索单项式与多项式相乘的法则的过程,体现
了哪些思想方法?
课堂小结
1.计算2x(3x2+1)的结果正确的是( ).
A. 5x3+2x2 B. 6x + 1
C. 6x +2x D. 6x2+2x
2.化简(-3a+ b)·(-7ab2)的结果是( ).
A.21a2b2+14ab3 B.21a2b2- ab3
C.-21a2b2+14ab3 D. -21a2b2+ ab3
7
2
7
2
1
2
C
B
巩固提高
3.计算(-3x)·(2x2-5x-1)的结果是 ( ).
A. -6x2-15x2 - 3x B. -6x3+15x2+3x
C. -6x+15x2 D. -6x3+15x2-1
4.要使x(x+a)+3x-2b=x2+5x+4成立,
则a,b的值分别为 ( ).
A.-2, -2 B.2,2
C.2, -2 D.-2,2
B
C
5.若x3(3xm-2xn+4xk) =3x9-2x6+4x4,则
m,n,k 的值分别为 ( ).
A.6,3,1 B.3,6,1
C.2,1,3 D.2,3,1
A
6.计算:
(1)ab·(a+1)= ;
(2)(-2a)( a3 -1)= ;
(3) -3xy(-3x y +xy) = .
a b+ab
9x3y2-3x2y2
1
4
- a4+2a
1
2
7.已知2m-3n=-5,则代数式m(n-4)-n(m-6)
的值为 .
8.现规定一种运算a*b=ab+a-b,其中a,b为实
数则a*b+(b-a)*b= .
10
b2-b
=ab+a-b
+(b-a)b+(b-a)-b
9.某长方体的长3m-4,宽为2m,高为m,则它
的体积为 .
6m3-8m2
10.某同学在计算一个多项式乘以-3x2时,因抄
错运算符号,算成了加上-3x2,得到的结果
是x2-4x+1,那么正确的计算结果是多少
(x2- 4x+1)-(-3x )
正确的计算结果是
解:这个多项式是
(4x2-4x+1)(-3x2)
=4x2-4x+1
=-12x4+12x3-3x2.
今天作业
课本P105页第4、7题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
