14.1.4整式的乘法(3) 课件(共25张PPT)
文档属性
| 名称 | 14.1.4整式的乘法(3) 课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-10 17:56:05 | ||
图片预览





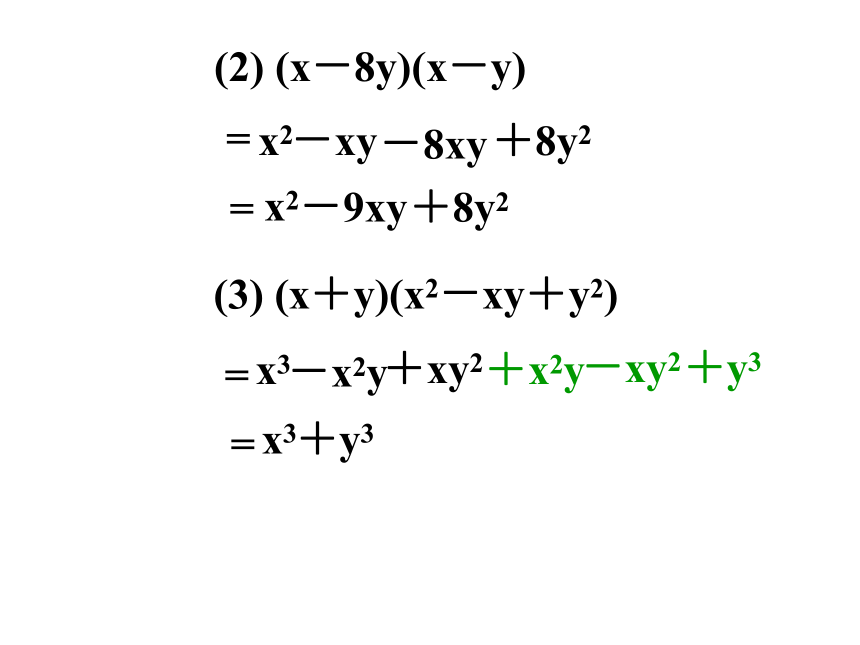
文档简介
(共25张PPT)
人教版 八年级上册
14.1.4 整式的乘法(3)
课件说明
本课是在学生学习了单项式与多项式相乘的基础上,
学习的“式”的另一种运算.它是将某些一元二次
方程整理成一般形式的基础,也是学习因式分解的
基础,它是本章的核心内容之一.
教学目标:
1.理解多项式与多项式相乘的法则,并能运用法则
进行计算.
2.理解算理,发展学生的运算能力和几何直观,体
会转化、数形结合和程序化思想.
教学重点:
多项式与多项式相乘的法则的概括与运用.
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
单项式乘以多项式的法则:
pb
pa
pc
+
+
(a+b+c)
p
=
复习旧知
计算:
(1)3a(5a-2b)= ;
(2) -ab(a-1)= .
15a2-6ab
-3a2b+ab
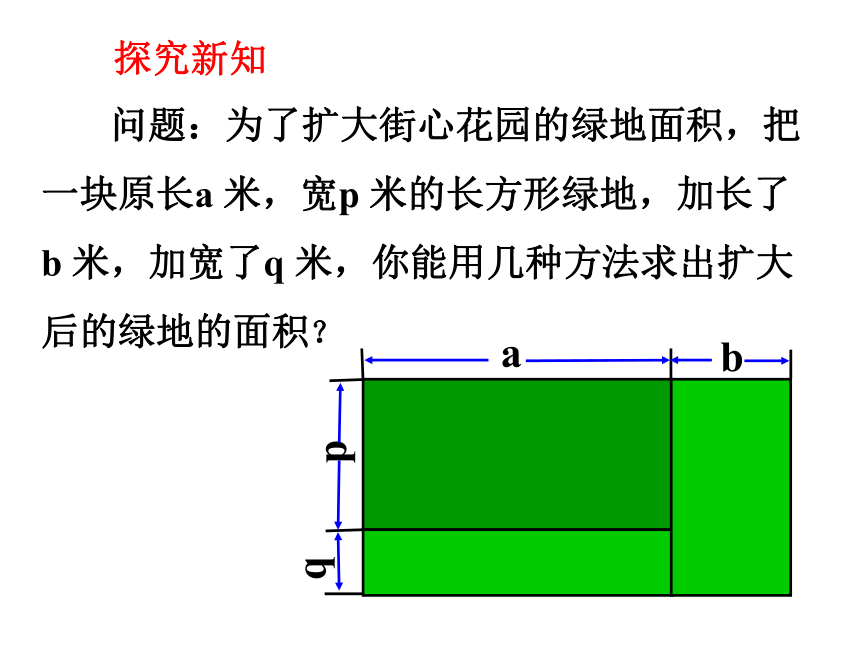
问题:为了扩大街心花园的绿地面积,把一块原长a 米,宽p 米的长方形绿地,加长了b 米,加宽了q 米,你能用几种方法求出扩大后的绿地的面积?
p
a
b
q
探究新知
a
b
q
p
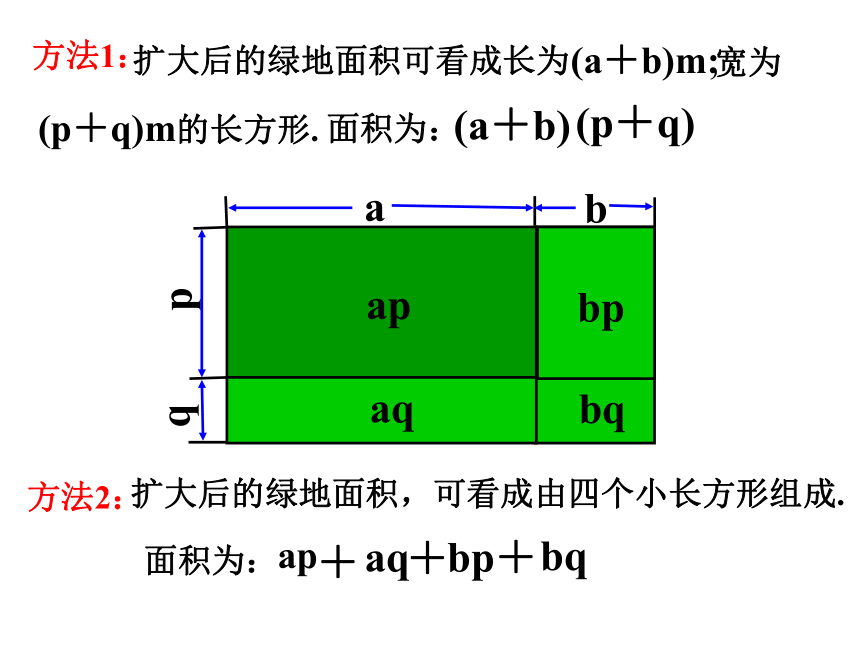
方法1:
扩大后的绿地面积可看成长为
方法2:
(a+b)m;
aq
面积为:
宽为
面积为:
扩大后的绿地面积,可看成由四个小长方形组成.
(p+q)m的长方形.
ap
bp
bq
ap
aq
bp
bq
(a+b)
(p+q)
+
+
+
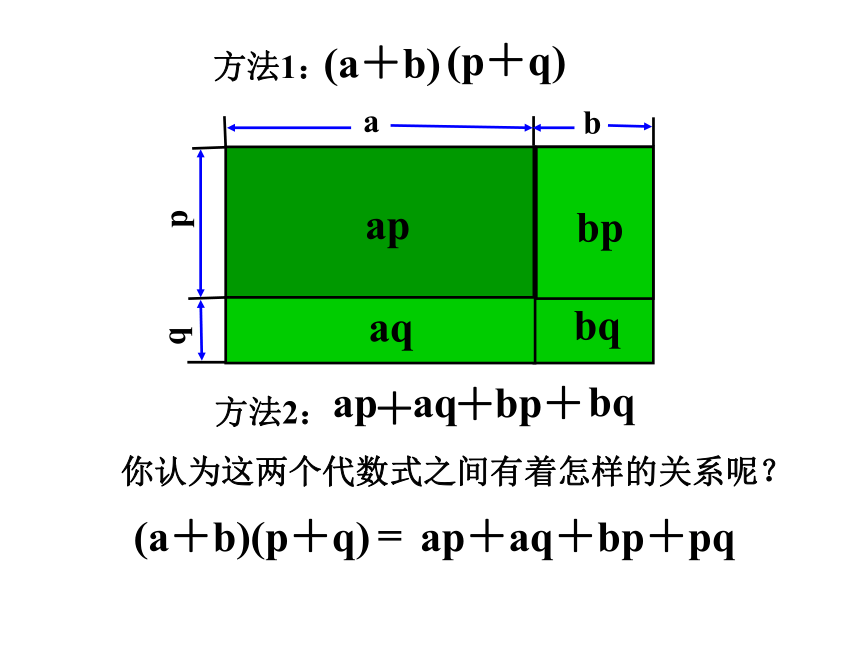
方法1:
方法2:
a
b
q
p
aq
ap
bp
bq
(a+b)
(p+q)
ap
aq
bp
bq
+
+
+
你认为这两个代数式之间有着怎样的关系呢?
(a+b)(p+q)
=
ap+aq+bp+pq
(a+b)(p+q)
=
ap+aq+bp+pq
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+b)(p+q)
=
ap
+aq
+bp
+pq
学习新知
例6 计算:
(2) (x-8y)(x-y) ;
(1) (3x+1) (x+2);
(3) (x+y)(x2-xy+y2).
解:
(1) (3x+1) (x+2)
=
=
=
●
(3x)
x
●
(3x )
2
●
1
x
1
×
2
+
+
+
3x2
+
6x
+
x
+
2
3x2+7x+2
例题解析
(2) (x-8y)(x-y)
=
x2
-xy
-8xy
+8y2
=
x2
-9xy
+8y2
(3) (x+y)(x2-xy+y2)
x3
-x2y
+xy2
+x2y
-xy2
+y3
=
=
x3
+y3
(1) (2x+1)(x+3)
(2) (m+2n)(3n-m)
(3) (a-1)2
(4) (a+3b)(a-3b)
=
=
2x2+6x
2x2+7x+3
=
=
3mn-m2
-m2+mn+6n2
=
=
=
=
=
(a-1)(a-1)
a2-a
a2-2a+1
a2-3ab
a2-9b2
+ x+3
+6n2-2mn
-a+1
+ 3ab-9b2
练习巩固
(5) (2x2-1) (x-4)
(6) (x2+2x+3) (2x-5)
=
=
=
2x3-8x2-x+4
2x3-5x2
+4x2-10x
+6x-15
2x3-x2-4x-15
解方程或不等式:
(1)(x-3)(x+8)=(x+4)(x-7)+2(x+ 5)
x2+5x-24
=x2-3x-28
+2x+10
解:
x2+5x-24
=x2-x-18
6x=6
x=1
例题解析
(2)2x(x - 4)>(x-3)(x-2)+(x+2)(x-6)
解方程:
1-(2x+1)(x-2)=x2-(3x-1)(x+3)-11.
2x2-8x
>x2-5x+6
+x2 -4x-12
解:
2x2-8x
>2x2-9x-12
x>-12
1-(2x2-3x-2)=
x2-(3x2+8x-3)-11.
1-2x2+3x+2=
x2-3x2-8x+3-11.
11x=11
x=-1
解:
学以致用
(1) (x+2)(x+3)
(2) (x-4)(x+1)
(3) (y+4)(y-2)
(4) (y-5) (y-3).
=
=
=
=
=
=
=
=
x2 +3x + 2x +6
x2+5x+6
x2 + x -4x-4
x2-3x-4
y2-2y+4y-8
y2+2y-8
y2-3y -5y +15
y2-8y+15.
根据上述求解过程,观察计算结果的各项系数与原式中的系数有怎样的关系?
计算并思考
(1) (x+2)(x+3)
(2) (x-4)(x+1)
(3) (y+4)(y-2)
(4) (y-5) (y-3).
=
=
=
=
x2+5x+6
x2-3x-4
y2+2y-8
y2-8y+15.
计算并思考
分别含有一个相同字母的项和一个常数项的两个一次二项式相乘,得到的积是同一字母的二次三项式,它的二次项是由两个因式中的一次项相乘得到的;它的一次项是由两个因式中的常数项分别乘另一个因式中的一次项后,合并同类项得到的;它的常数项等于两个因式中常数项的积.
(1)本节课学习了哪些主要内容?
(2)在运用多项式与多项式相乘的法则时,你认为
应该注意哪些问题?
(3)举例说明在探索多项式与多项式相乘的法则的
过程中,体现了哪些思想方法?
课堂小结
巩固提高
1.计算(a-3)(a+2)的结果是( ).
A. a2-6 B.a2-a-6
C.a2-a+6 D. a2+a-6
2.若(x-3)(x+8)=x2+mx+n,则m,n
的值是 ( ).
A.m=5,n= -24 B.m=-5,n=-24
C.m=5,n=24 D.m=-5,n=24
B
A
3.若(x+m)(x+6)的展开式中不含x的一次项,
则m的值为( ).
A.0 B.6 C. -6 D. -6 或 6
4.若(x+2)(x-1)=x2 +mx+n,则m+n的
值为( ).
A. -2 B. -1 C. 1 D. 2
C
B
6.李老师做了一个长方形教具,其中一边长为
2a+b,另一边长a-b.则该长方形的面积为( ).
A.6a+b B.2a2-ab-b2
C. 3a D.10a-b
B
5.计算代数式(3a+2)(a -a)的结果中,二次项
系数是( ).
A. -3 B. -2 C. -1 D. 2
C
7.计算:
(1)(3x-1)(x-2)= ;
(2)(x-3y)(x+7y)= .
8.若(x+3)(x-4)=ax2 +bx+c,则abc= .
12
3x2-7x+2
x2+4xy-21y2
9.商店经营一种产品,定价为12元/件,每天
能售出8件,而每降价x元,则每天可多售
(x+2)件,则降价x元后,每天的销售额为
元.
(-x2+2x+120)
10..甲、乙二人分别计算(2x+a)(3x+b),甲抄
错了第一个因式中a的符号,得到的结果是
6x+11x-10;乙漏抄了第二个因式中x的系
数,得到的结果是2x2-9x+10.
(1)求a,b的值;(2)求这个算式的正确结果.
解:(1)
(2x-a)(3x+b)=
由题意,得
6x2+(2b-3a)x-ab
=6x2+11x-10
(2x+a)(x+b)=
=2x2-9x+1
2x2+(2b+a)x+ab
2b-3a=11
2b+a= - 9
a= - 5
b=-2
由(1),得
(2)
(2x-5)(3x-2)=
6x2-4x
-15x+10
=6x2-19x+10
∴
∴
今天作业
课本P105页第5、8题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 八年级上册
14.1.4 整式的乘法(3)
课件说明
本课是在学生学习了单项式与多项式相乘的基础上,
学习的“式”的另一种运算.它是将某些一元二次
方程整理成一般形式的基础,也是学习因式分解的
基础,它是本章的核心内容之一.
教学目标:
1.理解多项式与多项式相乘的法则,并能运用法则
进行计算.
2.理解算理,发展学生的运算能力和几何直观,体
会转化、数形结合和程序化思想.
教学重点:
多项式与多项式相乘的法则的概括与运用.
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
单项式乘以多项式的法则:
pb
pa
pc
+
+
(a+b+c)
p
=
复习旧知
计算:
(1)3a(5a-2b)= ;
(2) -ab(a-1)= .
15a2-6ab
-3a2b+ab
问题:为了扩大街心花园的绿地面积,把一块原长a 米,宽p 米的长方形绿地,加长了b 米,加宽了q 米,你能用几种方法求出扩大后的绿地的面积?
p
a
b
q
探究新知
a
b
q
p
方法1:
扩大后的绿地面积可看成长为
方法2:
(a+b)m;
aq
面积为:
宽为
面积为:
扩大后的绿地面积,可看成由四个小长方形组成.
(p+q)m的长方形.
ap
bp
bq
ap
aq
bp
bq
(a+b)
(p+q)
+
+
+
方法1:
方法2:
a
b
q
p
aq
ap
bp
bq
(a+b)
(p+q)
ap
aq
bp
bq
+
+
+
你认为这两个代数式之间有着怎样的关系呢?
(a+b)(p+q)
=
ap+aq+bp+pq
(a+b)(p+q)
=
ap+aq+bp+pq
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+b)(p+q)
=
ap
+aq
+bp
+pq
学习新知
例6 计算:
(2) (x-8y)(x-y) ;
(1) (3x+1) (x+2);
(3) (x+y)(x2-xy+y2).
解:
(1) (3x+1) (x+2)
=
=
=
●
(3x)
x
●
(3x )
2
●
1
x
1
×
2
+
+
+
3x2
+
6x
+
x
+
2
3x2+7x+2
例题解析
(2) (x-8y)(x-y)
=
x2
-xy
-8xy
+8y2
=
x2
-9xy
+8y2
(3) (x+y)(x2-xy+y2)
x3
-x2y
+xy2
+x2y
-xy2
+y3
=
=
x3
+y3
(1) (2x+1)(x+3)
(2) (m+2n)(3n-m)
(3) (a-1)2
(4) (a+3b)(a-3b)
=
=
2x2+6x
2x2+7x+3
=
=
3mn-m2
-m2+mn+6n2
=
=
=
=
=
(a-1)(a-1)
a2-a
a2-2a+1
a2-3ab
a2-9b2
+ x+3
+6n2-2mn
-a+1
+ 3ab-9b2
练习巩固
(5) (2x2-1) (x-4)
(6) (x2+2x+3) (2x-5)
=
=
=
2x3-8x2-x+4
2x3-5x2
+4x2-10x
+6x-15
2x3-x2-4x-15
解方程或不等式:
(1)(x-3)(x+8)=(x+4)(x-7)+2(x+ 5)
x2+5x-24
=x2-3x-28
+2x+10
解:
x2+5x-24
=x2-x-18
6x=6
x=1
例题解析
(2)2x(x - 4)>(x-3)(x-2)+(x+2)(x-6)
解方程:
1-(2x+1)(x-2)=x2-(3x-1)(x+3)-11.
2x2-8x
>x2-5x+6
+x2 -4x-12
解:
2x2-8x
>2x2-9x-12
x>-12
1-(2x2-3x-2)=
x2-(3x2+8x-3)-11.
1-2x2+3x+2=
x2-3x2-8x+3-11.
11x=11
x=-1
解:
学以致用
(1) (x+2)(x+3)
(2) (x-4)(x+1)
(3) (y+4)(y-2)
(4) (y-5) (y-3).
=
=
=
=
=
=
=
=
x2 +3x + 2x +6
x2+5x+6
x2 + x -4x-4
x2-3x-4
y2-2y+4y-8
y2+2y-8
y2-3y -5y +15
y2-8y+15.
根据上述求解过程,观察计算结果的各项系数与原式中的系数有怎样的关系?
计算并思考
(1) (x+2)(x+3)
(2) (x-4)(x+1)
(3) (y+4)(y-2)
(4) (y-5) (y-3).
=
=
=
=
x2+5x+6
x2-3x-4
y2+2y-8
y2-8y+15.
计算并思考
分别含有一个相同字母的项和一个常数项的两个一次二项式相乘,得到的积是同一字母的二次三项式,它的二次项是由两个因式中的一次项相乘得到的;它的一次项是由两个因式中的常数项分别乘另一个因式中的一次项后,合并同类项得到的;它的常数项等于两个因式中常数项的积.
(1)本节课学习了哪些主要内容?
(2)在运用多项式与多项式相乘的法则时,你认为
应该注意哪些问题?
(3)举例说明在探索多项式与多项式相乘的法则的
过程中,体现了哪些思想方法?
课堂小结
巩固提高
1.计算(a-3)(a+2)的结果是( ).
A. a2-6 B.a2-a-6
C.a2-a+6 D. a2+a-6
2.若(x-3)(x+8)=x2+mx+n,则m,n
的值是 ( ).
A.m=5,n= -24 B.m=-5,n=-24
C.m=5,n=24 D.m=-5,n=24
B
A
3.若(x+m)(x+6)的展开式中不含x的一次项,
则m的值为( ).
A.0 B.6 C. -6 D. -6 或 6
4.若(x+2)(x-1)=x2 +mx+n,则m+n的
值为( ).
A. -2 B. -1 C. 1 D. 2
C
B
6.李老师做了一个长方形教具,其中一边长为
2a+b,另一边长a-b.则该长方形的面积为( ).
A.6a+b B.2a2-ab-b2
C. 3a D.10a-b
B
5.计算代数式(3a+2)(a -a)的结果中,二次项
系数是( ).
A. -3 B. -2 C. -1 D. 2
C
7.计算:
(1)(3x-1)(x-2)= ;
(2)(x-3y)(x+7y)= .
8.若(x+3)(x-4)=ax2 +bx+c,则abc= .
12
3x2-7x+2
x2+4xy-21y2
9.商店经营一种产品,定价为12元/件,每天
能售出8件,而每降价x元,则每天可多售
(x+2)件,则降价x元后,每天的销售额为
元.
(-x2+2x+120)
10..甲、乙二人分别计算(2x+a)(3x+b),甲抄
错了第一个因式中a的符号,得到的结果是
6x+11x-10;乙漏抄了第二个因式中x的系
数,得到的结果是2x2-9x+10.
(1)求a,b的值;(2)求这个算式的正确结果.
解:(1)
(2x-a)(3x+b)=
由题意,得
6x2+(2b-3a)x-ab
=6x2+11x-10
(2x+a)(x+b)=
=2x2-9x+1
2x2+(2b+a)x+ab
2b-3a=11
2b+a= - 9
a= - 5
b=-2
由(1),得
(2)
(2x-5)(3x-2)=
6x2-4x
-15x+10
=6x2-19x+10
∴
∴
今天作业
课本P105页第5、8题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
