1.3正弦、余弦的诱导公式(2)[上学期]
文档属性
| 名称 | 1.3正弦、余弦的诱导公式(2)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 106.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-03 13:47:00 | ||
图片预览






文档简介
课件21张PPT。1.3 正弦、余弦的诱导公式 (1)(公式一) sin(α+k·360°) = sinα
cos(α+k·360°) = cosα
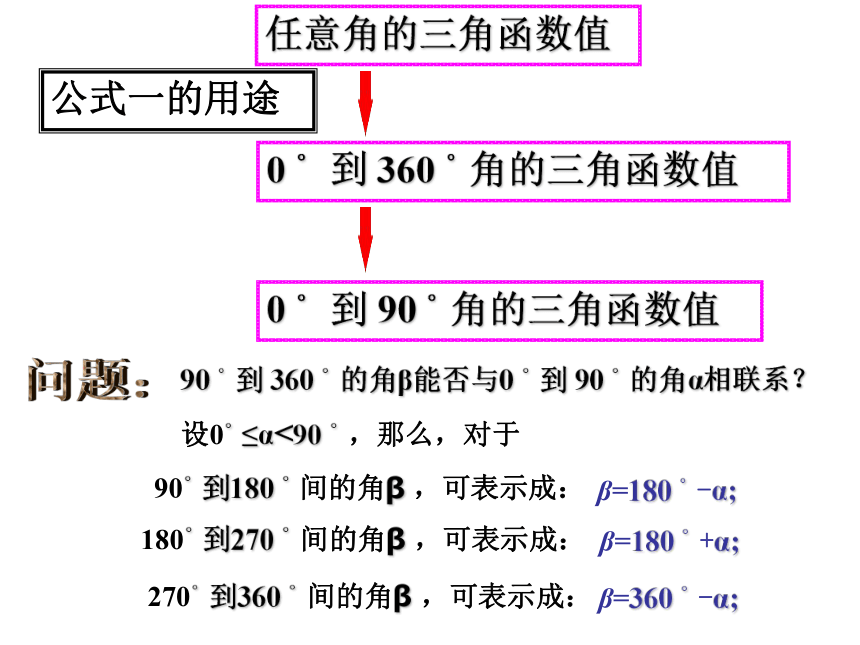
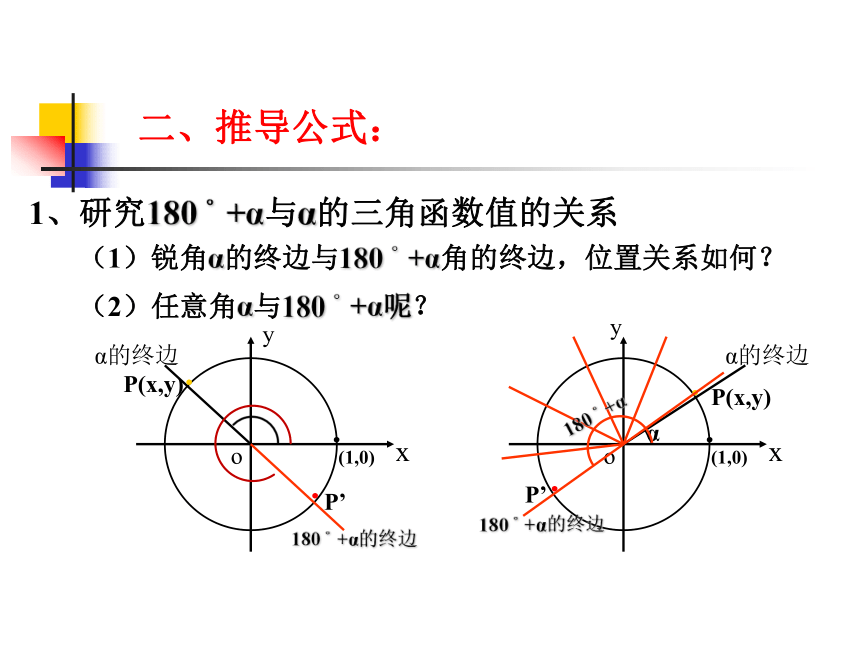
tan(α+k·360°) = tanα 其中 k∈Z终边相同的角的同一三角函数的值相等一、复习:公式一的用途任意角的三角函数值0 ° 到 360 °角的三角函数值0 ° 到 90 °角的三角函数值问题:90 °到 360 °的角β能否与0 °到 90 °的角α相联系?设0°≤α<90 °,那么,对于90°到180 °间的角β ,可表示成:180°到270 °间的角β ,可表示成:270°到360 °间的角β ,可表示成:β=180 °-α;β=180 °+α;β=360 °-α;1、研究180 °+α与α的三角函数值的关系(1)锐角α的终边与180 °+α角的终边,位置关系如何?(2)任意角α与180 °+α呢?180 °+α180 °+α的终边180 °+α的终边二、推导公式:由分析可得:因此 sin(180 °+α) = -sinα
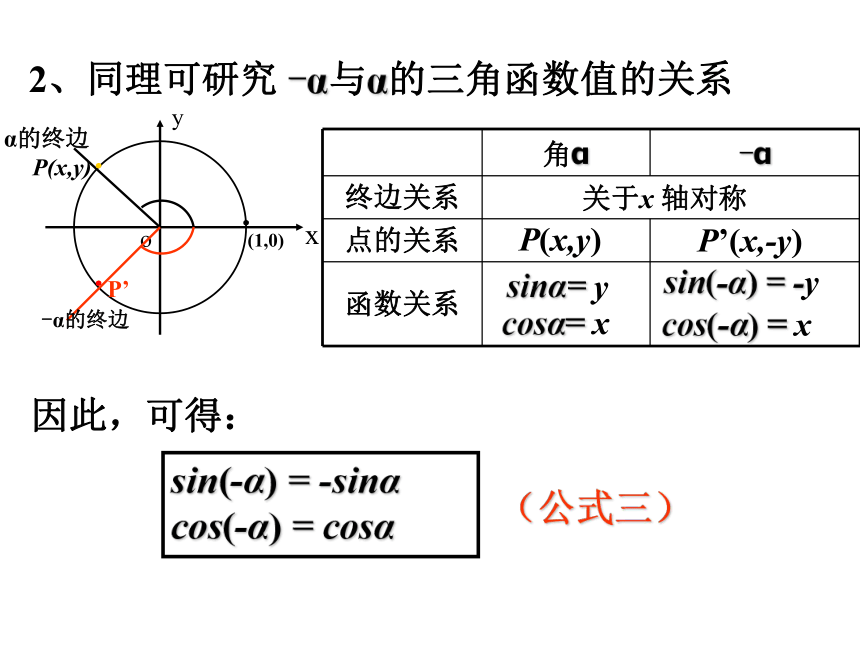
cos(180 °+α) = -cosα(公式二)角180 °+α的终边就是角α终边的反向延长线P(x,y)P’(-x,-y)sinα= ycosα= xsin(180 °+α)= -ycos(180 °+α)= -x2、同理可研究 -α与α的三角函数值的关系-α的终边因此,可得:sin(-α) = -sinα cos(-α) = cosα(公式三)关于x 轴对称P(x,y)P’(x,-y)sinα= ycosα= xsin(-α) = -ycos(-α) = x公式一: sin(α+k·360°) = sinα
cos(α+k·360°) = cosα
tan(α+k·360°) = tanα 其中 k∈Zsin(-α) = -sinα cos(-α) = cosα公式三: sin(180 °+α) = -sinα
cos(180 °+α) = -cosα公式二:练习: 化简下列各式:sin(180°-α)cos(180°-α)sin(360°-α)cos(360°-α)= sin[180°+(-α)]= -sin(-α)= sinα= cos[180°+(-α)]= -cos(-α)= -cosα= sin[360°+(-α)]= sin(-α)= -sinα= cos[360°+(-α)]= cos(-α)= cosα公式四:公式五: sin(180 ° -α) = sinα
cos(180 ° -α) = -cosα sin(360 ° -α) = -sinα
cos(360 ° -α) = cosα公式五: sin(180 ° -α) = sinα
cos(180 ° -α) = -cosα公式四: sin(360 ° -α) = -sinα
cos(360 ° -α) = cosα公式一、二、三、四、五都叫做 诱导公式诱导公式小结口诀: “函数名不变,符号看象限”.公式四公式五 sin(180°- α) =
cos(180°-α) = sin(360° -α) =
cos(360° - α) = 公式一sin(α+k·360°) =
cos(α+k·360°) = 公式二公式三 sin(180°+ α) =
cos(180°+ α) = sin(-α) =
cos(- α) = +--++---++sinαcosαsinαcosαcosαsinαsinαcosαcosαsinα口诀: “函数名不变,
符号看象限”.解题一般步骤:任意负角的三角函数任意正角的三角函数0°到360°的角的三角函数锐角三角函数例1 求下列三角函数值:
(1) cos225 ° ;例2 化简:练习 化简:正切的诱导公式:正切的诱导公式:口诀: “函数名不变,符号看象限”.例3 已知解:∴ α是第一、四象限的角 .①若α是第一象限的角,则②若α是第四象限的角,则例4 已知解:课本 P31~32 练习
1,2,3 ,4.作业:课本 P32 习题1.3
1,2,3 .
cos(α+k·360°) = cosα
tan(α+k·360°) = tanα 其中 k∈Z终边相同的角的同一三角函数的值相等一、复习:公式一的用途任意角的三角函数值0 ° 到 360 °角的三角函数值0 ° 到 90 °角的三角函数值问题:90 °到 360 °的角β能否与0 °到 90 °的角α相联系?设0°≤α<90 °,那么,对于90°到180 °间的角β ,可表示成:180°到270 °间的角β ,可表示成:270°到360 °间的角β ,可表示成:β=180 °-α;β=180 °+α;β=360 °-α;1、研究180 °+α与α的三角函数值的关系(1)锐角α的终边与180 °+α角的终边,位置关系如何?(2)任意角α与180 °+α呢?180 °+α180 °+α的终边180 °+α的终边二、推导公式:由分析可得:因此 sin(180 °+α) = -sinα
cos(180 °+α) = -cosα(公式二)角180 °+α的终边就是角α终边的反向延长线P(x,y)P’(-x,-y)sinα= ycosα= xsin(180 °+α)= -ycos(180 °+α)= -x2、同理可研究 -α与α的三角函数值的关系-α的终边因此,可得:sin(-α) = -sinα cos(-α) = cosα(公式三)关于x 轴对称P(x,y)P’(x,-y)sinα= ycosα= xsin(-α) = -ycos(-α) = x公式一: sin(α+k·360°) = sinα
cos(α+k·360°) = cosα
tan(α+k·360°) = tanα 其中 k∈Zsin(-α) = -sinα cos(-α) = cosα公式三: sin(180 °+α) = -sinα
cos(180 °+α) = -cosα公式二:练习: 化简下列各式:sin(180°-α)cos(180°-α)sin(360°-α)cos(360°-α)= sin[180°+(-α)]= -sin(-α)= sinα= cos[180°+(-α)]= -cos(-α)= -cosα= sin[360°+(-α)]= sin(-α)= -sinα= cos[360°+(-α)]= cos(-α)= cosα公式四:公式五: sin(180 ° -α) = sinα
cos(180 ° -α) = -cosα sin(360 ° -α) = -sinα
cos(360 ° -α) = cosα公式五: sin(180 ° -α) = sinα
cos(180 ° -α) = -cosα公式四: sin(360 ° -α) = -sinα
cos(360 ° -α) = cosα公式一、二、三、四、五都叫做 诱导公式诱导公式小结口诀: “函数名不变,符号看象限”.公式四公式五 sin(180°- α) =
cos(180°-α) = sin(360° -α) =
cos(360° - α) = 公式一sin(α+k·360°) =
cos(α+k·360°) = 公式二公式三 sin(180°+ α) =
cos(180°+ α) = sin(-α) =
cos(- α) = +--++---++sinαcosαsinαcosαcosαsinαsinαcosαcosαsinα口诀: “函数名不变,
符号看象限”.解题一般步骤:任意负角的三角函数任意正角的三角函数0°到360°的角的三角函数锐角三角函数例1 求下列三角函数值:
(1) cos225 ° ;例2 化简:练习 化简:正切的诱导公式:正切的诱导公式:口诀: “函数名不变,符号看象限”.例3 已知解:∴ α是第一、四象限的角 .①若α是第一象限的角,则②若α是第四象限的角,则例4 已知解:课本 P31~32 练习
1,2,3 ,4.作业:课本 P32 习题1.3
1,2,3 .
