两角差的余弦公式[上学期]

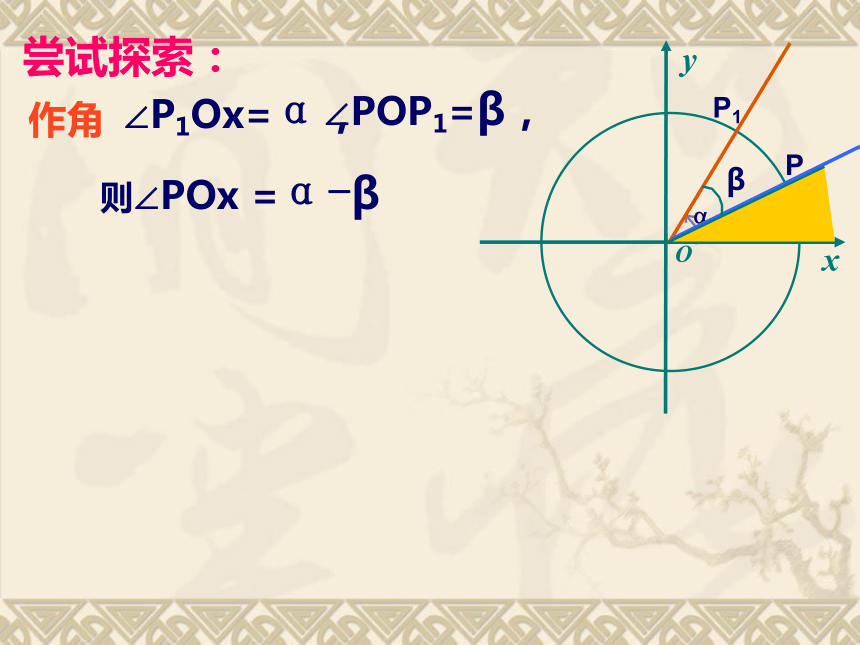
课件12张PPT。第三章 三角恒等变换3.1 两角和与差的正弦、余弦和正切公式 3.1.1 两角差的余弦公式 问题1:你认为cos(α-β)=cosα-cosβ成立吗?问题2:你认为cos(α-β)=cosαcosβ+sinαsinβ成立吗?尝试探索：作角P1∠P1Ox=α，P∠POP1=β，则∠POx =α-βOxy作角P∠POP1=β，则∠POx =α-β找线P1∠P1Ox=α，尝试探索：β?P1PMABC即:思考：以上结果为α、β、α-β均为锐角，且α>β的情况下得到的，此式是否对任意角都成立呢？β?cos(α-β)=cosαcosβ+sinαsinβ②怎样用向量数量积的运算和定义得到结果？①结合图形，思考应选用哪几个向量？ 当α-β为任意角时，由诱导公式，总可以找到一个角?∈[0,2?),使cos?=cos(α-β)称为差角的余弦公式。简记为Cα-βcos(α-β)=cosαcosβ+sinαsinβ想一想：1，公式有何特点？你如何记忆？分析：怎样把15°表示成两个特殊角的差？解：1:已知四个单角函数值求差角的余弦。例1，利用差角余弦公式求cos15°的值.所以cos(α-β)＝ cosβcosα+sinβsinα2:已知两个单角函数值求差角的余弦。练习：课本P140 1, 2，3，4 题差角的余弦公式,cos(α-β)=cosαcosβ+sinαsinβ简记为Cα-β教材Ｐ150 1(1)(3),2,3