2023年新高考数学二轮复习真题源讲义之1.5.1第1讲 概率、统计、统计案例 课件(共42张PPT)
文档属性
| 名称 | 2023年新高考数学二轮复习真题源讲义之1.5.1第1讲 概率、统计、统计案例 课件(共42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-10 23:17:59 | ||
图片预览









文档简介
(共42张PPT)
第1讲 概率、统计、统计案例、
正态分布——小题备考
微专题1 用样本估计总体
微专题2 变量间的相关关系、统计案例
微专题3 概率问题
微专题1
用样本估计总体
『常考常用结论』
1.直方图的两个结论
(1)小长方形的面积=组距×=频率.
(2)各小长方形的面积之和等于1.
2.统计中的四个数字特征
(1)众数:在样本数据中,出现次数最多的那个数据.
(2)中位数:样本数据中,将数据按大小排列,位于最中间的数据.如果数据的个数为偶数,就取中间两个数据的平均数作为中位数.
(3)平均数:样本数据的算术平均数,即
=(x1+x2+…+xn).
(4)方差与标准差
方差:s2=[(x1-)2+(x2-)2+…+(xn-)2].
标准差:s=.
『保分题组训练』
1.[2021·广东江门一模]从一批零件中抽取80个,测量其直径(单位:mm),将所得数据分为9组:[5.31,5.33),[5.33,5.35),…,[5.45,5.47),[5.47,5.49],并整理得到频率分布直方图,则在被抽取的零件中,直径不小于5.43 mm的个数为( )
A.10 B.18 C.26 D.36
解析:由频率分布直方图可知,直径不小于5.43 mm的频率为(6.25+5+5)×0.02=0.325,
故在被抽取的零件中,直径不小于5.43 mm的个数为0.325×80=26个.
故选C.
C
2.[2021·福建龙岩模拟]平均数和中位数都描述了数据的集中趋势,它们的大小关系和数据的分布形态有关.如图所示的统计图,记这组数据的众数为M,中位数为N,平均数为P,则( )
A.N解析:由统计图可得,众数为M=5;
共有2+3+10+6+3+2+2+2=30个数据,处在中间位置的两个数据为5,6,所以中位数为N==5.5;
平均数P=≈5.97,
所以M故选B.
B
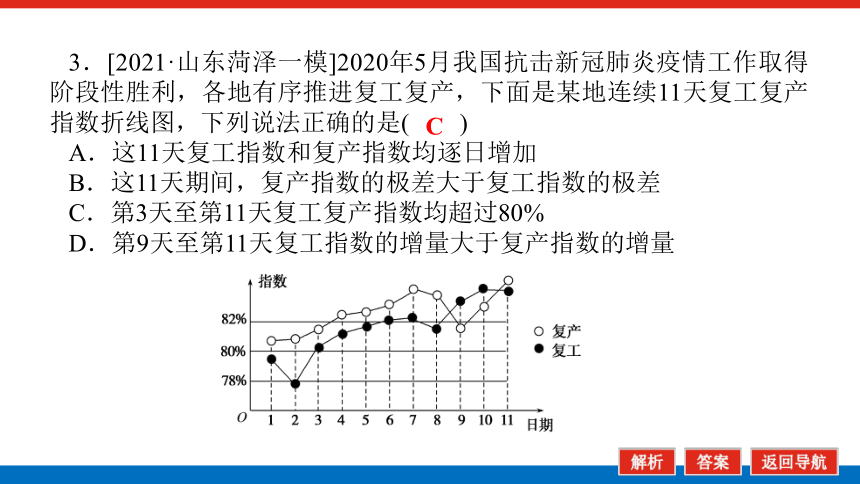
3.[2021·山东菏泽一模]2020年5月我国抗击新冠肺炎疫情工作取得阶段性胜利,各地有序推进复工复产,下面是某地连续11天复工复产指数折线图,下列说法正确的是( )
A.这11天复工指数和复产指数均逐日增加
B.这11天期间,复产指数的极差大于复工指数的极差
C.第3天至第11天复工复产指数均超过80%
D.第9天至第11天复工指数的增量大于复产指数的增量
C
解析:第8天比第7天的复工指数和复产指数均低,A错误;
这11天期间,复产指数的极差小于复工指数的极差:两者最高差不多,但最低的复工指数比复产指数低得多,B错误;
第3天至第11天复工复产指数均超过80%,C正确;
第9天至第11天复工指数的增量小于复产指数的增量,D错误.
故选C.
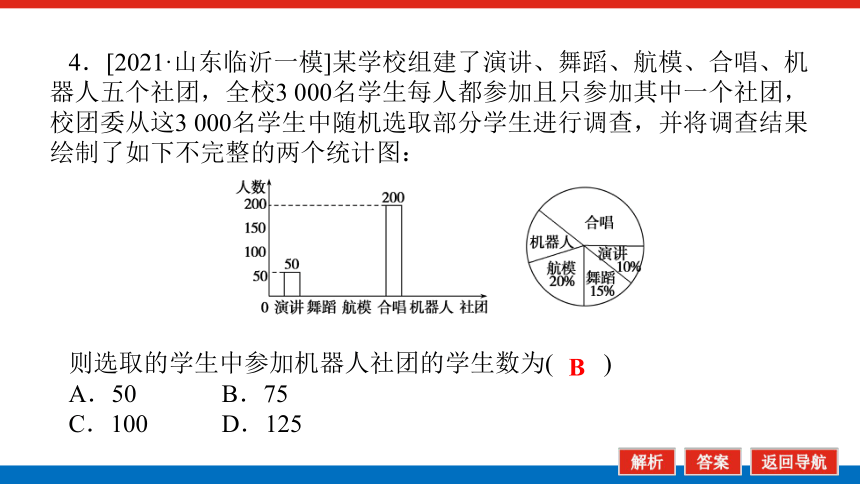
4.[2021·山东临沂一模]某学校组建了演讲、舞蹈、航模、合唱、机器人五个社团,全校3 000名学生每人都参加且只参加其中一个社团,校团委从这3 000名学生中随机选取部分学生进行调查,并将调查结果绘制了如下不完整的两个统计图:
则选取的学生中参加机器人社团的学生数为( )
A.50 B.75
C.100 D.125
B
解析:由条形统计图得抽到50名同学演讲,
由扇形统计图得抽到的学生中演讲同学占10%,
∴一共抽取的学生数为:n==500(人),
∴抽到的学生中合唱学生占:×100%=40%,
∴选取的学生中参加机器人社团的学生数为:
500×(1-40%-10%-15%-20%)=75(人).
故选B.
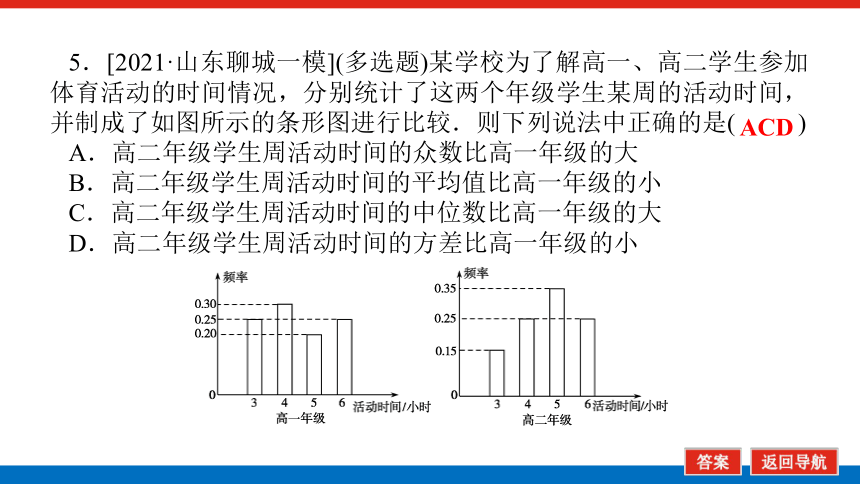
5.[2021·山东聊城一模](多选题)某学校为了解高一、高二学生参加体育活动的时间情况,分别统计了这两个年级学生某周的活动时间,并制成了如图所示的条形图进行比较.则下列说法中正确的是( )
A.高二年级学生周活动时间的众数比高一年级的大
B.高二年级学生周活动时间的平均值比高一年级的小
C.高二年级学生周活动时间的中位数比高一年级的大
D.高二年级学生周活动时间的方差比高一年级的小
ACD
【技法领悟】
众数、中位数、平均数与直方图的关系
1.众数为频率分布直方图中最高矩形的底边中点的横坐标.
2.中位数为平分频率分布直方图面积且垂直于横轴的直线与横轴交点的横坐标.
3.平均数等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之积的和.
微专题2
变量间的相关关系、统计案例
『常考常用结论』
1.方程=x+是两个具有线性相关关系的变量的一组数据(x1,y1),(x2,y2),…,(xn,yn)的回归方程,其中是待定参数,回归方程的斜率和截距分别为==,()是样本中心点,回归直线过样本中心点.
2.(1)正相关与负相关就看回归直线的斜率,斜率为正则为正相关,斜率为负则为负相关.
(2)样本相关系数r具有以下性质:r>0表示两个变量正相关,r<0表示两个变量负相关;|r|≤1,且|r|越接近于1,线性相关程度越强,|r|越接近于0,线性相关程度越弱.
3.“卡方公式”:χ2=,
n=a+b+c+d.
『保分题组训练』
1.已知变量x,y之间的经验回归方程为=-0.7x+10.3,且变量x,y之间的一组相关数据如表所示,则下列说法错误的是( )
A .变量x,y之间呈负相关关系
B.m=4
C.可以预测,当x=20时,=-3.7
D.该回归直线必过点
x 6 8 10 12
y 6 m 3 2
B
解析:A.由回归方程=-0.7x+10.3知=-0.7<0,所以变量x,y之间呈负相关关系,故正确;
B.因为=(6+8+10+12)=9.则=-0.7×9+10.3=4,所以=(6+m+3+2)=(11+m)=4,解得m=5,故错误;
C.当x=20时,=-0.7×20+10.3=-3.7,故正确;
D.由B知:=9,=4,所以回归直线必过点,故正确.
故选B.
2.[2021·湖南永州模拟](多选题)某校对“学生性别和喜欢锻炼是否有关”作了一次调查,其中被调查的男女生人数相同,男生喜欢锻炼的人数占男生总人数的,女生喜欢锻炼的人数占女生总人数的.若至少有95%的把握认为“学生性别和喜欢锻炼有关”,则被调查学生中男生的人数可能为( )
附:χ2=(n=a+b+c+d)
A.35 B.40
C.45 D.50
α 0.050 0.010
xα 3.841 6.635
CD
解析:由题意被调查的男女生人数相同,设男生的人数为:5n,n∈N*,由题意可列出2×2列联表:
χ2=
==.
由于有95%的把握认为“学生性别和喜欢锻炼有关”,
所以3.841≤<6.635;
解得:8.066 1≤n<13.933 5,
则n的可能取值为:9、10、11、12、13;
则选项中被调查学生中男生的人数可能为45或50.
故选CD.
男生 女生 合计
喜欢锻炼 4n 3n 7n
不喜欢锻炼 n 2n 3n
合计 5n 5n 10n
3.[2021·山东烟台一模]2021年2月25日,全国脱贫攻坚总结表彰大会在北京举行,习近平总书记庄严宣告我国脱贫攻坚战取得了全面胜利,已知在党委政府精准扶贫政策下,自2017年起某地区贫困户第x年的年人均收入y(单位:万元)的统计数据如下表:
根据上表可得回归方程=x+中的为0.3,据此模型预报该地区贫困户2021年的年人均收入为__________(单位:万元).
年份 2017 2018 2019 2020
年份编号x 1 2 3 4
年人均收入y 0.6 0.8 1.1 1.5
解析:由题=2.5,=1,将(2.5,1)代入=0.3x+中,得=0.25,
2021年对应的年份编号x为5,将x=5代入=0.3x+0.25中,得=1.75.
1.75
4.[2021·山东青岛一模]某驾驶员培训学校为对比了解“科目二”的培训过程采用大密度集中培训与周末分散培训两种方式的效果,调查了105名学员,统计结果为:接受大密度集中培训的55个学员中有45名学员一次考试通过,接受周末分散培训的学员一次考试通过的有30个.根据统
计结果,认为“能否一次考试通过与是否集中培训有关”犯错误的概率不超过________.
附:χ2=.
α 0.05 0.025 0.010 0.001
xα 3.841 5.024 6.635 10.828
0.025
解析:2×2列联表如下:
∴χ2==6.109>5.024,
∴认为“能否一次考试通过与是否集中培训有关”犯错误的概率不超过0.025.
通过 未通过 总计
集中培训 45 10 55
分散培训 30 20 50
总计 75 30 105
5.[2021·临沂一模]蟋蟀鸣叫可以说是大自然优美、和谐的音乐,蟋蟀鸣叫的频率y(每分钟鸣叫的次数)与气温x(单位:℃)存在着较强的线性相关关系.某地研究人员根据当地的气温和蟋蟀鸣叫的频率得到了如下数据:
利用如表中的数据求得经验回归方程为=x+,若利用该方程知当该地的气温为30 ℃时,蟋蟀每分钟鸣叫次数的预报值为68,则的值为________.
x(℃) 21 22 23 24 25 26 27
y(次数/分钟) 24 28 31 39 43 47 54
5
解析:=×(21+22+23+24+25+26+27)=24,=×(24+28+31+39+43+47+54)=38,
∴样本中心点为(24,38),
∴38=×24+①,
∵当该地的气温为30 ℃时,蟋蟀每分钟鸣叫次数的预报值为68,
∴68=×30+②,
由①②解得=5.
【技法领悟】
统计案例的两个关键
1.求回归直线方程的关键
(1)正确理解的计算公式并能准确地进行运算.
(2)根据样本数据作出散点图来确定两个变量之间是否具有相关关系,若具有线性相关关系,则可通过线性回归方程估计和预测变量的值.
2.独立性检验的关键
(1)根据2×2列联表准确计算χ2,若2×2列联表没有列出来,要先列出此表.
(2)χ2的观测值越大,对应假设事件H0成立的概率越小,H0不成立的概率越大.
微专题3
概率问题
『常考常用结论』
1.古典概型的概率公式
P(A)=
2.条件概率:P(B|A)==
3.全概率:P(B)=
4.相互独立事件的概率:
P(AB)=P(A)P(B)
5.二项分布:
Pn(k)=pk(1-p)n-k;E(X)=np;D(X)=np(1-p)
6.超几何分布:
P(X=k)=,k=m,m+1,m+2,…,r.
其中n,N,M∈N*,M≤N,n≤N,m=max{0,n-N+M},r=min{n,M}.
E(X)=np=
7.正态分布:
(1)正态分布的定义及表示
f(x)=,x∈R.
其中μ∈R,σ>0为参数.
显然,对任意的x∈R,f(x)>0,它的图象在x轴的上方.可以证明x轴和曲线之间的区域的面积为1.我们称f(x)为正态密度函数,称它的图象为正态密度曲线,简称正态曲线,如图所示.若随机变量X的概率分布密度函数为f(x),则称随机变量X服从正态分布(normal distribution),记为X~N(μ,σ2).特别地,当μ=0,σ=1时,称随机变量X服从标准正态分布.
若X~N(μ,σ2),则如图所示,X取值不超过x的概率P(X≤x)为图中区域A的面积,而P(a≤X≤b)为区域B的面积.
(2)正态总体三个基本概念值
①P(μ-σ≤X≤μ+σ)≈0.682 7;
②P(μ-2σ≤X≤μ+2σ)≈0.954 5;
③P(μ-3σ≤X≤μ+3σ)≈0.997 3.
『保分题组训练』
1.[2021·辽宁锦州一模]在一个排列a1,a2,a3,…,an(n∈N+)中,任取两个数ap,aq(p,q∈N+且paq,则称这两个数ap,aq为该排列的一个逆序,一个排列中逆序的总数称为这个排列的逆序数.在排列2,4,3,1,5中任取两数,则这组数是逆序的概率是( )
A. B. C. D.
解析:在排列2,4,3,1,5中任取两数,构成排列的基本事件有:
,共10个,这组数是逆序包含的基本事件有:,共4个,
则这组数是逆序的概率是P==.故选B.
B
2.[2021·山东潍坊一模]接种疫苗是预防和控制传染病最经济、有效的公共卫生干预措施.根据实验数据,人在接种某种病毒疫苗后,有80%不会感染这种病毒,若有4人接种了这种疫苗,则最多1人被感染的概率为( )
A. B. C. D.
解析:P=0.2×0.83+0.84=.故选A.
A
3.[2021·河北石家庄一模]已知随机变量X服从正态分布N(10,σ2),若P(X<8)=0.23,则P(X<12)=________.
4.[2021·湖北武汉市高三模拟]抛掷3个骰子,事件A为“三个骰子向上的点数互不相同”,事件B为“其中恰好有一个骰子向上的点数
为2”,则P=________.
解析:∵随机变量X服从正态分布N(10,σ2),P(X<8)=0.23,
∴P(X>12)=0.23,
∴P(X<12)=1-0.23=0.77.
解析:由题意,事件B发生的概率为P==,
事件AB发生的概率为P===,
因此P==.
0.77
『提分题组训练』
1.[2021·湖南六校联考]某地安排4名工作人员随机分到3个村参加“脱贫攻坚”帮扶活动,且每个人只去一个村,则每个村至少有一名工作人员的概率为( )
A. B.
C. D.
A
解析:4人随机去3个村的可能情况有34=81种,
每个人只去一个村,则每个村至少有一名工作人员有=36种,
故P==.
故选A.
2.[2021·山东滨州二模](多选题)为庆祝建党100周年,讴歌中华民族实现伟大复兴的奋斗历程,增进全体党员干部职工对党史知识的了解,某单位组织开展党史知识竞赛活动,以支部为单位参加比赛,某支部在5道党史题中(有3道选择题和2道填空题),不放回地依次随机抽取2道题作答,设事件A为“第1次抽到选择题”,事件B为“第2次抽到选择题”,则下列结论中正确的是( )
A.P= B.P=
C.P= D.P=
ABC
解析:P==,故A正确;
P==,故B正确;
P===,故C正确;
P==,P==,P===,故D错误.故选ABC.
3.[2021·河北张家口一模](多选题)袋子中有2个黑球,1个白球,现从袋子中有放回地随机取球4次,取到白球记0分,黑球记1分,记4次取球的总分数为X,则( )
A.X~B B.P(X=2)=
C.X的期望E(X)= D.X的方差D(X)=
ACD
解析:由于每次取球互不影响,故所有结果有4类:
①4次全是白球,X=0,记其概率为P(X=0)==;
②4次只有1次是黑球,X=1,记其概率为P(X=1)==;
③4次只有2次是黑球,X=2,记其概率为P(X=2)==;
④4次只有3次是黑球,X=3,记其概率为P(X=3)==;
⑤4次全是黑球,X=4,记其概率为P(X=4)==.
故X~B,故A正确,B错误;
因为X~B,所以X的期望E(X)=4×=,故C正确;
因为X~B,所以X的方差D(X)=4×=,故D正确.故选ACD.
4.[2021·河北沧州二模]三分损益法是古代中国发明制定音律时所用的生律法.三分损益包含“三分损一”“三分益一”两层含义,三分损一是指将原有长度作3等分而减去其1份,即原有长度×=生得长度;而三分益一则是指将原有长度作3等分而增添其1份,即原有长度×=生得长度,两种方法可以交替运用、连续运用,各音律就得以辗转相生,假设能发出第一个基准音的乐器的长度为243,每次损益的概率为,则
经过5次三分损益得到的乐器的长度为128的概率为________.
解析:设5次三分损益中有k次三分损一,所以243×k×5-k=128,解得k=3.
故所求概率为5==.
【技法领悟】
1.求复杂事件概率的两种方法:
(1)直接法:正确分析复杂事件的构成,将复杂事件转化为几个彼此互斥的事件的和事件或几个相互独立事件同时发生的积事件或一独立重复试验问题,然后用相应概率公式求解.
(2)间接法:当复杂事件正面情况比较多,反面情况较少,则可利用其对立事件进行求解.对于“至少”“至多”等问题往往也用这种方法求解.
2.利用正态曲线的对称性求概率的策略:
(1)解题的关键是利用对称轴x=μ确定所求概率对应的随机变量的区间与已知概率对应的随机变量的区间的关系,必要时,可借助图形判断.
(2)对于正态分布N(μ,σ2),由x=μ是正态曲线的对称轴知:
①对任意的a,有P(X<μ-a)=P(X>μ+a);
②P(X③P(a(3)对于特殊区间求概率一定要掌握服从N(μ,σ2)的随机变量X在三个特殊区间的取值概率,将所求问题向P(μ-σ≤X≤μ+σ),P(μ-2σ≤X≤μ+2σ),P(μ-3σ≤X≤μ+3σ)转化,然后利用特定值求出相应概率.同时,要充分利用正态曲线的对称性和曲线与x轴之间的面积为1这些特殊性质.
第1讲 概率、统计、统计案例、
正态分布——小题备考
微专题1 用样本估计总体
微专题2 变量间的相关关系、统计案例
微专题3 概率问题
微专题1
用样本估计总体
『常考常用结论』
1.直方图的两个结论
(1)小长方形的面积=组距×=频率.
(2)各小长方形的面积之和等于1.
2.统计中的四个数字特征
(1)众数:在样本数据中,出现次数最多的那个数据.
(2)中位数:样本数据中,将数据按大小排列,位于最中间的数据.如果数据的个数为偶数,就取中间两个数据的平均数作为中位数.
(3)平均数:样本数据的算术平均数,即
=(x1+x2+…+xn).
(4)方差与标准差
方差:s2=[(x1-)2+(x2-)2+…+(xn-)2].
标准差:s=.
『保分题组训练』
1.[2021·广东江门一模]从一批零件中抽取80个,测量其直径(单位:mm),将所得数据分为9组:[5.31,5.33),[5.33,5.35),…,[5.45,5.47),[5.47,5.49],并整理得到频率分布直方图,则在被抽取的零件中,直径不小于5.43 mm的个数为( )
A.10 B.18 C.26 D.36
解析:由频率分布直方图可知,直径不小于5.43 mm的频率为(6.25+5+5)×0.02=0.325,
故在被抽取的零件中,直径不小于5.43 mm的个数为0.325×80=26个.
故选C.
C
2.[2021·福建龙岩模拟]平均数和中位数都描述了数据的集中趋势,它们的大小关系和数据的分布形态有关.如图所示的统计图,记这组数据的众数为M,中位数为N,平均数为P,则( )
A.N
共有2+3+10+6+3+2+2+2=30个数据,处在中间位置的两个数据为5,6,所以中位数为N==5.5;
平均数P=≈5.97,
所以M
B
3.[2021·山东菏泽一模]2020年5月我国抗击新冠肺炎疫情工作取得阶段性胜利,各地有序推进复工复产,下面是某地连续11天复工复产指数折线图,下列说法正确的是( )
A.这11天复工指数和复产指数均逐日增加
B.这11天期间,复产指数的极差大于复工指数的极差
C.第3天至第11天复工复产指数均超过80%
D.第9天至第11天复工指数的增量大于复产指数的增量
C
解析:第8天比第7天的复工指数和复产指数均低,A错误;
这11天期间,复产指数的极差小于复工指数的极差:两者最高差不多,但最低的复工指数比复产指数低得多,B错误;
第3天至第11天复工复产指数均超过80%,C正确;
第9天至第11天复工指数的增量小于复产指数的增量,D错误.
故选C.
4.[2021·山东临沂一模]某学校组建了演讲、舞蹈、航模、合唱、机器人五个社团,全校3 000名学生每人都参加且只参加其中一个社团,校团委从这3 000名学生中随机选取部分学生进行调查,并将调查结果绘制了如下不完整的两个统计图:
则选取的学生中参加机器人社团的学生数为( )
A.50 B.75
C.100 D.125
B
解析:由条形统计图得抽到50名同学演讲,
由扇形统计图得抽到的学生中演讲同学占10%,
∴一共抽取的学生数为:n==500(人),
∴抽到的学生中合唱学生占:×100%=40%,
∴选取的学生中参加机器人社团的学生数为:
500×(1-40%-10%-15%-20%)=75(人).
故选B.
5.[2021·山东聊城一模](多选题)某学校为了解高一、高二学生参加体育活动的时间情况,分别统计了这两个年级学生某周的活动时间,并制成了如图所示的条形图进行比较.则下列说法中正确的是( )
A.高二年级学生周活动时间的众数比高一年级的大
B.高二年级学生周活动时间的平均值比高一年级的小
C.高二年级学生周活动时间的中位数比高一年级的大
D.高二年级学生周活动时间的方差比高一年级的小
ACD
【技法领悟】
众数、中位数、平均数与直方图的关系
1.众数为频率分布直方图中最高矩形的底边中点的横坐标.
2.中位数为平分频率分布直方图面积且垂直于横轴的直线与横轴交点的横坐标.
3.平均数等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之积的和.
微专题2
变量间的相关关系、统计案例
『常考常用结论』
1.方程=x+是两个具有线性相关关系的变量的一组数据(x1,y1),(x2,y2),…,(xn,yn)的回归方程,其中是待定参数,回归方程的斜率和截距分别为==,()是样本中心点,回归直线过样本中心点.
2.(1)正相关与负相关就看回归直线的斜率,斜率为正则为正相关,斜率为负则为负相关.
(2)样本相关系数r具有以下性质:r>0表示两个变量正相关,r<0表示两个变量负相关;|r|≤1,且|r|越接近于1,线性相关程度越强,|r|越接近于0,线性相关程度越弱.
3.“卡方公式”:χ2=,
n=a+b+c+d.
『保分题组训练』
1.已知变量x,y之间的经验回归方程为=-0.7x+10.3,且变量x,y之间的一组相关数据如表所示,则下列说法错误的是( )
A .变量x,y之间呈负相关关系
B.m=4
C.可以预测,当x=20时,=-3.7
D.该回归直线必过点
x 6 8 10 12
y 6 m 3 2
B
解析:A.由回归方程=-0.7x+10.3知=-0.7<0,所以变量x,y之间呈负相关关系,故正确;
B.因为=(6+8+10+12)=9.则=-0.7×9+10.3=4,所以=(6+m+3+2)=(11+m)=4,解得m=5,故错误;
C.当x=20时,=-0.7×20+10.3=-3.7,故正确;
D.由B知:=9,=4,所以回归直线必过点,故正确.
故选B.
2.[2021·湖南永州模拟](多选题)某校对“学生性别和喜欢锻炼是否有关”作了一次调查,其中被调查的男女生人数相同,男生喜欢锻炼的人数占男生总人数的,女生喜欢锻炼的人数占女生总人数的.若至少有95%的把握认为“学生性别和喜欢锻炼有关”,则被调查学生中男生的人数可能为( )
附:χ2=(n=a+b+c+d)
A.35 B.40
C.45 D.50
α 0.050 0.010
xα 3.841 6.635
CD
解析:由题意被调查的男女生人数相同,设男生的人数为:5n,n∈N*,由题意可列出2×2列联表:
χ2=
==.
由于有95%的把握认为“学生性别和喜欢锻炼有关”,
所以3.841≤<6.635;
解得:8.066 1≤n<13.933 5,
则n的可能取值为:9、10、11、12、13;
则选项中被调查学生中男生的人数可能为45或50.
故选CD.
男生 女生 合计
喜欢锻炼 4n 3n 7n
不喜欢锻炼 n 2n 3n
合计 5n 5n 10n
3.[2021·山东烟台一模]2021年2月25日,全国脱贫攻坚总结表彰大会在北京举行,习近平总书记庄严宣告我国脱贫攻坚战取得了全面胜利,已知在党委政府精准扶贫政策下,自2017年起某地区贫困户第x年的年人均收入y(单位:万元)的统计数据如下表:
根据上表可得回归方程=x+中的为0.3,据此模型预报该地区贫困户2021年的年人均收入为__________(单位:万元).
年份 2017 2018 2019 2020
年份编号x 1 2 3 4
年人均收入y 0.6 0.8 1.1 1.5
解析:由题=2.5,=1,将(2.5,1)代入=0.3x+中,得=0.25,
2021年对应的年份编号x为5,将x=5代入=0.3x+0.25中,得=1.75.
1.75
4.[2021·山东青岛一模]某驾驶员培训学校为对比了解“科目二”的培训过程采用大密度集中培训与周末分散培训两种方式的效果,调查了105名学员,统计结果为:接受大密度集中培训的55个学员中有45名学员一次考试通过,接受周末分散培训的学员一次考试通过的有30个.根据统
计结果,认为“能否一次考试通过与是否集中培训有关”犯错误的概率不超过________.
附:χ2=.
α 0.05 0.025 0.010 0.001
xα 3.841 5.024 6.635 10.828
0.025
解析:2×2列联表如下:
∴χ2==6.109>5.024,
∴认为“能否一次考试通过与是否集中培训有关”犯错误的概率不超过0.025.
通过 未通过 总计
集中培训 45 10 55
分散培训 30 20 50
总计 75 30 105
5.[2021·临沂一模]蟋蟀鸣叫可以说是大自然优美、和谐的音乐,蟋蟀鸣叫的频率y(每分钟鸣叫的次数)与气温x(单位:℃)存在着较强的线性相关关系.某地研究人员根据当地的气温和蟋蟀鸣叫的频率得到了如下数据:
利用如表中的数据求得经验回归方程为=x+,若利用该方程知当该地的气温为30 ℃时,蟋蟀每分钟鸣叫次数的预报值为68,则的值为________.
x(℃) 21 22 23 24 25 26 27
y(次数/分钟) 24 28 31 39 43 47 54
5
解析:=×(21+22+23+24+25+26+27)=24,=×(24+28+31+39+43+47+54)=38,
∴样本中心点为(24,38),
∴38=×24+①,
∵当该地的气温为30 ℃时,蟋蟀每分钟鸣叫次数的预报值为68,
∴68=×30+②,
由①②解得=5.
【技法领悟】
统计案例的两个关键
1.求回归直线方程的关键
(1)正确理解的计算公式并能准确地进行运算.
(2)根据样本数据作出散点图来确定两个变量之间是否具有相关关系,若具有线性相关关系,则可通过线性回归方程估计和预测变量的值.
2.独立性检验的关键
(1)根据2×2列联表准确计算χ2,若2×2列联表没有列出来,要先列出此表.
(2)χ2的观测值越大,对应假设事件H0成立的概率越小,H0不成立的概率越大.
微专题3
概率问题
『常考常用结论』
1.古典概型的概率公式
P(A)=
2.条件概率:P(B|A)==
3.全概率:P(B)=
4.相互独立事件的概率:
P(AB)=P(A)P(B)
5.二项分布:
Pn(k)=pk(1-p)n-k;E(X)=np;D(X)=np(1-p)
6.超几何分布:
P(X=k)=,k=m,m+1,m+2,…,r.
其中n,N,M∈N*,M≤N,n≤N,m=max{0,n-N+M},r=min{n,M}.
E(X)=np=
7.正态分布:
(1)正态分布的定义及表示
f(x)=,x∈R.
其中μ∈R,σ>0为参数.
显然,对任意的x∈R,f(x)>0,它的图象在x轴的上方.可以证明x轴和曲线之间的区域的面积为1.我们称f(x)为正态密度函数,称它的图象为正态密度曲线,简称正态曲线,如图所示.若随机变量X的概率分布密度函数为f(x),则称随机变量X服从正态分布(normal distribution),记为X~N(μ,σ2).特别地,当μ=0,σ=1时,称随机变量X服从标准正态分布.
若X~N(μ,σ2),则如图所示,X取值不超过x的概率P(X≤x)为图中区域A的面积,而P(a≤X≤b)为区域B的面积.
(2)正态总体三个基本概念值
①P(μ-σ≤X≤μ+σ)≈0.682 7;
②P(μ-2σ≤X≤μ+2σ)≈0.954 5;
③P(μ-3σ≤X≤μ+3σ)≈0.997 3.
『保分题组训练』
1.[2021·辽宁锦州一模]在一个排列a1,a2,a3,…,an(n∈N+)中,任取两个数ap,aq(p,q∈N+且p
A. B. C. D.
解析:在排列2,4,3,1,5中任取两数,构成排列的基本事件有:
,共10个,这组数是逆序包含的基本事件有:,共4个,
则这组数是逆序的概率是P==.故选B.
B
2.[2021·山东潍坊一模]接种疫苗是预防和控制传染病最经济、有效的公共卫生干预措施.根据实验数据,人在接种某种病毒疫苗后,有80%不会感染这种病毒,若有4人接种了这种疫苗,则最多1人被感染的概率为( )
A. B. C. D.
解析:P=0.2×0.83+0.84=.故选A.
A
3.[2021·河北石家庄一模]已知随机变量X服从正态分布N(10,σ2),若P(X<8)=0.23,则P(X<12)=________.
4.[2021·湖北武汉市高三模拟]抛掷3个骰子,事件A为“三个骰子向上的点数互不相同”,事件B为“其中恰好有一个骰子向上的点数
为2”,则P=________.
解析:∵随机变量X服从正态分布N(10,σ2),P(X<8)=0.23,
∴P(X>12)=0.23,
∴P(X<12)=1-0.23=0.77.
解析:由题意,事件B发生的概率为P==,
事件AB发生的概率为P===,
因此P==.
0.77
『提分题组训练』
1.[2021·湖南六校联考]某地安排4名工作人员随机分到3个村参加“脱贫攻坚”帮扶活动,且每个人只去一个村,则每个村至少有一名工作人员的概率为( )
A. B.
C. D.
A
解析:4人随机去3个村的可能情况有34=81种,
每个人只去一个村,则每个村至少有一名工作人员有=36种,
故P==.
故选A.
2.[2021·山东滨州二模](多选题)为庆祝建党100周年,讴歌中华民族实现伟大复兴的奋斗历程,增进全体党员干部职工对党史知识的了解,某单位组织开展党史知识竞赛活动,以支部为单位参加比赛,某支部在5道党史题中(有3道选择题和2道填空题),不放回地依次随机抽取2道题作答,设事件A为“第1次抽到选择题”,事件B为“第2次抽到选择题”,则下列结论中正确的是( )
A.P= B.P=
C.P= D.P=
ABC
解析:P==,故A正确;
P==,故B正确;
P===,故C正确;
P==,P==,P===,故D错误.故选ABC.
3.[2021·河北张家口一模](多选题)袋子中有2个黑球,1个白球,现从袋子中有放回地随机取球4次,取到白球记0分,黑球记1分,记4次取球的总分数为X,则( )
A.X~B B.P(X=2)=
C.X的期望E(X)= D.X的方差D(X)=
ACD
解析:由于每次取球互不影响,故所有结果有4类:
①4次全是白球,X=0,记其概率为P(X=0)==;
②4次只有1次是黑球,X=1,记其概率为P(X=1)==;
③4次只有2次是黑球,X=2,记其概率为P(X=2)==;
④4次只有3次是黑球,X=3,记其概率为P(X=3)==;
⑤4次全是黑球,X=4,记其概率为P(X=4)==.
故X~B,故A正确,B错误;
因为X~B,所以X的期望E(X)=4×=,故C正确;
因为X~B,所以X的方差D(X)=4×=,故D正确.故选ACD.
4.[2021·河北沧州二模]三分损益法是古代中国发明制定音律时所用的生律法.三分损益包含“三分损一”“三分益一”两层含义,三分损一是指将原有长度作3等分而减去其1份,即原有长度×=生得长度;而三分益一则是指将原有长度作3等分而增添其1份,即原有长度×=生得长度,两种方法可以交替运用、连续运用,各音律就得以辗转相生,假设能发出第一个基准音的乐器的长度为243,每次损益的概率为,则
经过5次三分损益得到的乐器的长度为128的概率为________.
解析:设5次三分损益中有k次三分损一,所以243×k×5-k=128,解得k=3.
故所求概率为5==.
【技法领悟】
1.求复杂事件概率的两种方法:
(1)直接法:正确分析复杂事件的构成,将复杂事件转化为几个彼此互斥的事件的和事件或几个相互独立事件同时发生的积事件或一独立重复试验问题,然后用相应概率公式求解.
(2)间接法:当复杂事件正面情况比较多,反面情况较少,则可利用其对立事件进行求解.对于“至少”“至多”等问题往往也用这种方法求解.
2.利用正态曲线的对称性求概率的策略:
(1)解题的关键是利用对称轴x=μ确定所求概率对应的随机变量的区间与已知概率对应的随机变量的区间的关系,必要时,可借助图形判断.
(2)对于正态分布N(μ,σ2),由x=μ是正态曲线的对称轴知:
①对任意的a,有P(X<μ-a)=P(X>μ+a);
②P(X
同课章节目录
