任意角的三角函数2[上学期]
图片预览









文档简介
课件30张PPT。任意角的三角函数 2、象限角:注:如果角的终边在坐标轴上,则该角不是象限角。3、所有与角 终边相同的角,连同角 在内,构成集合:(角度制)(弧度制)原点x轴的非负半轴角的终边(除端点外)在第几象限,我们就说这个角是第几象限角。正负一.复习 4、什么是1弧度的角?长度等于半径长的弧所对的圆心角。5、弧度的计算:角度的符号由旋转
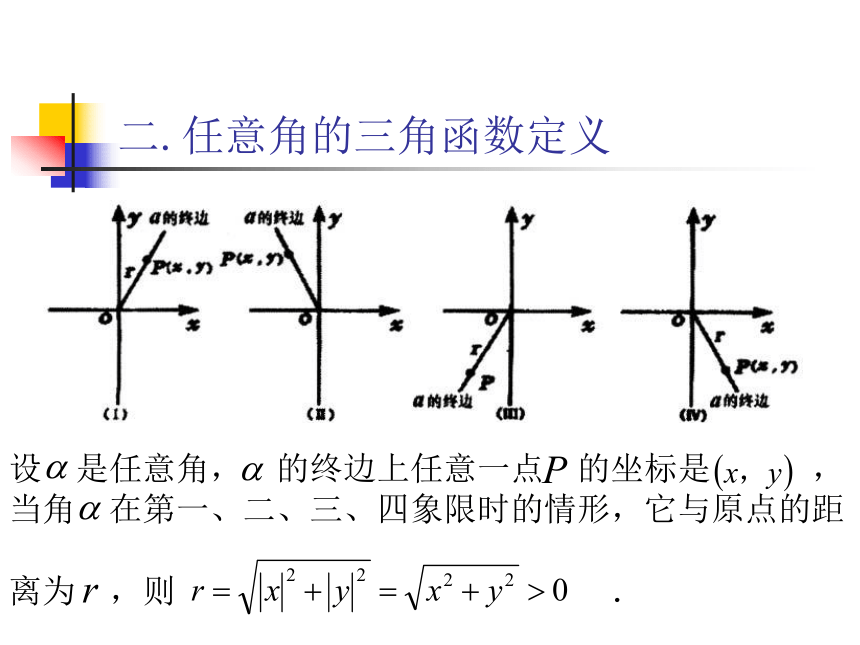
方向确定6、角度与弧度的换算:7、扇形面积公式: 角的范围已经推广,那么对任一角 是否也能像锐角一样定义其四种三角函数呢? 我们已经学习过锐角三角函数,知道它们都是以锐角 为自变量,以比值为函数值,定义了角 的正弦、余弦、正切、余切的三角函数,本节课我们研究当角 是一个任意角时,其三角函数的定义及其几何表示. 二.任意角的三角函数定义 设 是任意角, 的终边上任意一点 的坐标是 ,当角 在第一、二、三、四象限时的情形,它与原点的距
离为 ,则 . ①比值 叫做 的正弦,记作 ,即 .②比值 叫做 的余弦,记作 ,即 .定义:③比值 叫做 的正切,记作 ,即 .提问: 对于确定的角 ,这三个比值的大小和 点在角 的终边上的位置是否有关呢? 观察当 时, 的终边在 轴上,此
时终边上任一点 的横坐标 都等于0,所以 无
意义,除此之外,对于确定的角 ,上面三个比值都是惟一确定的.把上面定义中三个比的前项、后项交换,那么得到另外三个定义. ④比值 叫做 的余切,记作 ,则 .⑤比值 叫做 的正割,记作 ,则 .⑥比值 叫做 的余割,记作 ,则 . 我们把正弦、余弦,正切、余切,正割及余割都看
成是以角为自变量,以比值为函数值的函数,以上六种
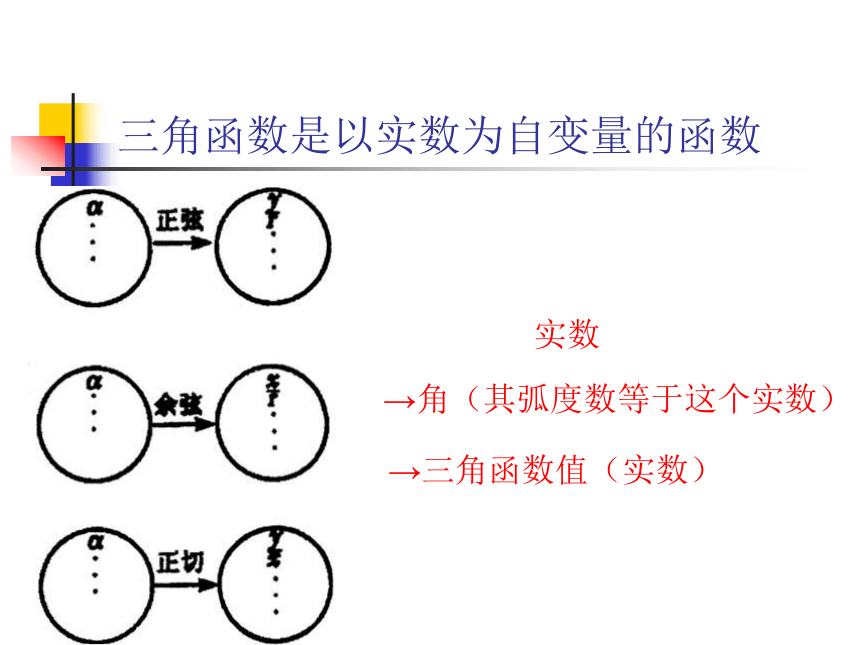
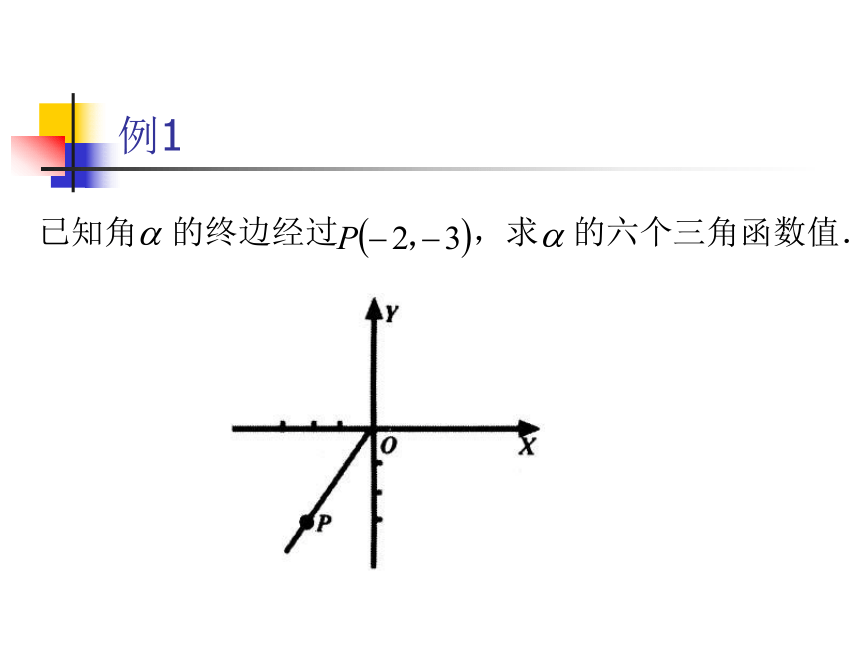
函数统称三角函数.三角函数是以实数为自变量的函数 例1 已知角 的终边经过 ,求 的六个三角函数值.提问:分 , 两种情形讨论.例2 探究:据任意角的三角函数定义,正弦,余弦,正切函数在弧度制下的定义域与这三种函数的值在各象限的符号如何?由三角函数的定义,可以知道:
终边相同的角的同一三角函数的值相等.由此得到诱导公式一:据诱导公式一把大角的三角函数化为小角的三角函数,
再据角所在象限确定角的三角函数值的符号.1.有向线段2、三角函数线、单位圆(圆心在原点,半径为单位长度的圆)三.任意角的三角函数的 (几何表示)----三角函数线带有方向的线段(方向由端点字母的顺序决定)MP(x,y)A(1,0)TMP是正弦线OM是余弦线 AT是正切线规定:与坐标轴同向为正,反向为负如若OA=2则AO=-22.三角函数线MPATMP是正弦线OM是余弦线 AT是正切线MPATMPATPMAT 当角 的终边在 轴上时,正弦线、正切线分别
变成一个点; 当角 的终边在 轴上时,余弦线变成一个点,正切线不存在.有向线段MP为正弦线
有向线段OM为余弦线
有向线段AT为正切线
三角函数线(前提是:角的顶点在坐标原点,始边与x轴的正半轴重合)例3 例4 求证:当 为锐角时, .课堂练习 (1)角 的终边在直线 上,求 的六个三角函数值.(3)说明 的理由 .(2)函数 的定义域是( ). A. B. C. D.反馈训练 (1)若角 终边上有一点 ,则下列函数值不存在
的是( ).A.B.C.D.(4)若角 的终边过点 ,且 ,(3)若 , 都有意义,则.则 .本课小结 利用定义求三角函数值,首先要建立直角坐标系,角α顶点和始边要按既定的位置设置.角的三角函数定义式,其实是比例的化身,它的背后是相似形在支称着,不过这个定义具有一般性,如轴上角的三角函数,如果没有定义作为论据,欲求其函数性就不是很容易. 分类讨论(角位置)是三角函数求值过程中,使用频率非常高的一个数学思想,而分类标准往往是四个象限及四个坐标半轴.
方向确定6、角度与弧度的换算:7、扇形面积公式: 角的范围已经推广,那么对任一角 是否也能像锐角一样定义其四种三角函数呢? 我们已经学习过锐角三角函数,知道它们都是以锐角 为自变量,以比值为函数值,定义了角 的正弦、余弦、正切、余切的三角函数,本节课我们研究当角 是一个任意角时,其三角函数的定义及其几何表示. 二.任意角的三角函数定义 设 是任意角, 的终边上任意一点 的坐标是 ,当角 在第一、二、三、四象限时的情形,它与原点的距
离为 ,则 . ①比值 叫做 的正弦,记作 ,即 .②比值 叫做 的余弦,记作 ,即 .定义:③比值 叫做 的正切,记作 ,即 .提问: 对于确定的角 ,这三个比值的大小和 点在角 的终边上的位置是否有关呢? 观察当 时, 的终边在 轴上,此
时终边上任一点 的横坐标 都等于0,所以 无
意义,除此之外,对于确定的角 ,上面三个比值都是惟一确定的.把上面定义中三个比的前项、后项交换,那么得到另外三个定义. ④比值 叫做 的余切,记作 ,则 .⑤比值 叫做 的正割,记作 ,则 .⑥比值 叫做 的余割,记作 ,则 . 我们把正弦、余弦,正切、余切,正割及余割都看
成是以角为自变量,以比值为函数值的函数,以上六种
函数统称三角函数.三角函数是以实数为自变量的函数 例1 已知角 的终边经过 ,求 的六个三角函数值.提问:分 , 两种情形讨论.例2 探究:据任意角的三角函数定义,正弦,余弦,正切函数在弧度制下的定义域与这三种函数的值在各象限的符号如何?由三角函数的定义,可以知道:
终边相同的角的同一三角函数的值相等.由此得到诱导公式一:据诱导公式一把大角的三角函数化为小角的三角函数,
再据角所在象限确定角的三角函数值的符号.1.有向线段2、三角函数线、单位圆(圆心在原点,半径为单位长度的圆)三.任意角的三角函数的 (几何表示)----三角函数线带有方向的线段(方向由端点字母的顺序决定)MP(x,y)A(1,0)TMP是正弦线OM是余弦线 AT是正切线规定:与坐标轴同向为正,反向为负如若OA=2则AO=-22.三角函数线MPATMP是正弦线OM是余弦线 AT是正切线MPATMPATPMAT 当角 的终边在 轴上时,正弦线、正切线分别
变成一个点; 当角 的终边在 轴上时,余弦线变成一个点,正切线不存在.有向线段MP为正弦线
有向线段OM为余弦线
有向线段AT为正切线
三角函数线(前提是:角的顶点在坐标原点,始边与x轴的正半轴重合)例3 例4 求证:当 为锐角时, .课堂练习 (1)角 的终边在直线 上,求 的六个三角函数值.(3)说明 的理由 .(2)函数 的定义域是( ). A. B. C. D.反馈训练 (1)若角 终边上有一点 ,则下列函数值不存在
的是( ).A.B.C.D.(4)若角 的终边过点 ,且 ,(3)若 , 都有意义,则.则 .本课小结 利用定义求三角函数值,首先要建立直角坐标系,角α顶点和始边要按既定的位置设置.角的三角函数定义式,其实是比例的化身,它的背后是相似形在支称着,不过这个定义具有一般性,如轴上角的三角函数,如果没有定义作为论据,欲求其函数性就不是很容易. 分类讨论(角位置)是三角函数求值过程中,使用频率非常高的一个数学思想,而分类标准往往是四个象限及四个坐标半轴.
