苏教版(2019)高中数学必修第一册 《第四章指数与对数》章末复习精品课件(共33张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学必修第一册 《第四章指数与对数》章末复习精品课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-11 21:28:47 | ||
图片预览











文档简介
(共33张PPT)
苏教版同步教材精品课件
《指数与对数》章末复习
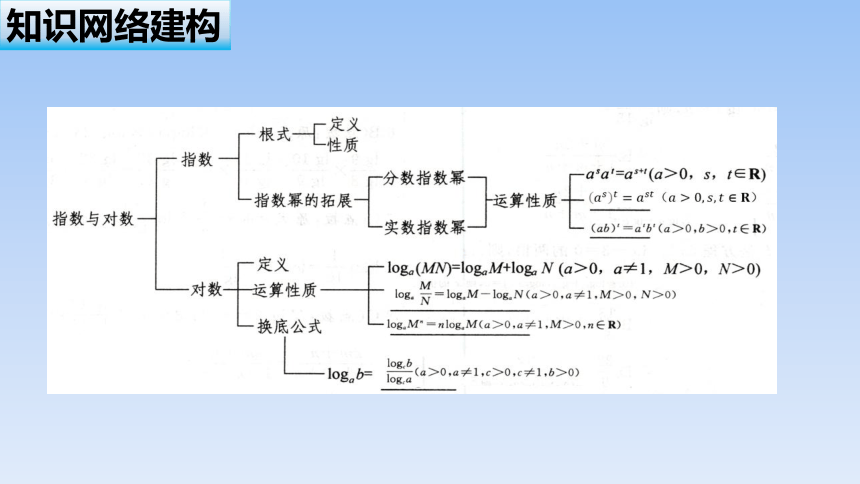
知识网络建构
指数幂运算的一般原则:
(1)有括号的先算括号里面的,无括号的先做指数运算.
(2)先乘除后加减,负指数幂化成正指数幂的倒数.
(3)底数是负数的,先确定符号;底数是小数的,先化成分数;底数是带分数的,先化成假分数.
(4)若是根式,应化为分数指数幂,尽可能用幂的形式表示,运用指数幂的运算性质来解答.
主要考查角度:
(1)根式与分数指数幂的互化;
(2)指数幂的化简;
(3)根式的性质与应用;
(4)分数指数幂的运算.
知识要点整合
一、指数的概念及运算
知识要点整合
典例剖析
解析
原式.
例1、_______(用分数指数幂表示)
例2、________.
解析
.
知识要点整合
典例剖析
分析
如果根式的被开方数不是的形式,先利用乘法公式将被开方数化成的形式,然后再利用的性质进行化简或运算.
例3、化简下列各式:
(1);(2);
(3).
解析
(1)
(2)原式
.
当,即时,
.
当,即时,
知识要点整合
典例剖析
如果根式的被开方数不是的形式,先利用乘法公式将被开方数化成的形式,然后再利用的性质进行化简或运算.
例3、化简下列各式:
(1);(2);
(3).
解析
(3)原式.
当时,原式;
当时,原式.
分析
知识要点整合
典例剖析
分析
依据下列法则运算:①先进行指数运算,在进行指数运算时可将底数化成幂的形式,再利用幂的乘方进行运算;②对于零次幂,直接运用得出结论;③底数为带分数的化成假分数,进而将底数化成幂的形式;④底数为小数的一般化成分数来运算;⑤先算乘方(开方),再算乘除,最后算加减.
例4、化简下列各式:
(1);
(2);
(3).
知识要点整合
典例剖析
例4、化简下列各式:
(1);
(2);
(3).
解析
(1)原式.
(2)原式.
(3)原式
.
条件求值问题是代数式求值问题中的常见题型,一般要结合已知条件先化简再求值.另外,要特别注意条件的应用,如条件中的隐含条件、整体代入等,可以简化解题过程.
解决此类问题的一般步骤:
(1)审题:从整体上把握已知条件和所求代数式的特点;
(2)化简:化简已知条件与所求代数式;
(3)求值:把条件代入求值.
主要考查角度:
(1)“已知值”的化简求值;
(2)利用“整体代入”化简求值.
知识要点整合
二、指数中条件因式的化简与求值
知识要点整合
典例剖析
分析
先对所求代数式进行化简,然后将x,y的值代入进行运算.
例5、已知,求的值.
解析
.
,
原式.
知识要点整合
典例剖析
例6、已知,则的值为 ( )
A.7 B. C. D.27
解析
由,两边平方得,则.
A
运算的一般思路:
(1)首先利用幂的运算把底数或真数进行变形,化成分数指数幂的形式,使幂的底数最简,然后正用对数运算性质化简合并.
(2)将对数式化为同底数对数的和、差、倍数运算,然后逆用对数的运算性质,转化为同底对数真数的积、商、幂的运算.
主要考查角度:
(1)对数式与指数式的互化;
(2)利用指数式与对数式的互化求变量x的值;
(3)对数的求值与化简;
(4)对数方程问题.
知识要点整合
三、对数的概念及运算对数
知识要点整合
典例剖析
例7、下列指数式与对数式互化不正确的一组是 ( )
A.=1与 B. 与
C.与 D. 与
解析
A.=1与 ;正确;
B. 与,正确;
C.应该化为,不正确;
D. 与,正确.
C
知识要点整合
典例剖析
分析
先将对数式化为指数式,然后利用指数幂的运算性质求解.
例8、求下列各式中x的值;
(1);(2).
解析
由(1)得,故.
(2)由得 ,故.
例9、计算_______.
解析
原式.
知识要点整合
典例剖析
例10、设的两根分别是,则 ( )
A. B. C. D.
解析
的两根分别是,
和是方程两个根,
则.
.
D
利用对数的换底公式以将不同底的对数问题化为同底的对数问题.解题时,首先要观察底数是否相同,若不同,则应用换底公式进行转化,然后运用对数的运算性质进行化简、计算换底时,要注意与题中条件结合,所取的底数要便于计算.
主要考查角度:
(1)利用换底公式求值;
(2)利用换底公式解决条件求值问题.
知识要点整合
四、对数换底公式的应用
知识要点整合
典例剖析
例11、设的值为 ( )
A. 18 B. C. D.
解析
原式.
C
例12、已知,则_________(用表示).
解析
.
数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养.主要包括:理解运算对象,掌握运算法则,探究运算思路,选择运算方法,设计运算程序,求得运算结果等.
本章内容中,利用指数幂的运算性质进行化简或计算,利用对数的运算性质进行化简或计算等方面涉及数学运算核心素养.
核心素养梳理
一、数学运算
典例剖析
例1、化简:.
解析
原式
.
分析
利用指数幂的运算性质进行化简.
核心素养梳理
典例剖析
例2、求值:(1);(2);
(3).
解析
(1)原式.
(2)原式.
(3)原式.
分析
利用对数的运算性质进行计算.
核心素养梳理
逻辑推理是指从一些事实和命题出发,依据规则推出其他命题的素养.逻辑推理主要表现为:掌握推理基本形式和规则,发现问题和提出命题,探索和表述论证过程,理解命题体系,有逻辑地表达与交流.
本章内容中,类比正整数指数幂理解有理数指数幂、无理数指数幂的概念,类比指数幂的运算性质学习对数的运算性质等方面涉及逻辑推理核心素养.
核心素养梳理
二、逻辑推理
典例剖析
例3、已知,求下列各式的值:
(1); (2); (3);(4).
解析
(1)由两边平方,得,即.
(2)由 ,得,即.
.
.
分析
从整体上寻找待求各式与条件的联系,进而整体代入求值.
核心素养梳理
典例剖析
例3、已知,求下列各式的值:
(1); (2); (3);(4).
解析
(3),
.
(4), ,即.
原式.
分析
从整体上寻找待求各式与条件的联系,进而整体代入求值.
核心素养梳理
指数与对数的运算在高考中很少单独命题,它往往作为解决指数函数与对数函数的工具,若单独命题多以填空题的形式出现,分值一般为5分,属于基础题.
高考真题再现
考点1 指数与对数运算
典例剖析
例1、(2015·安徽)______.
解析
.
高考真题再现
例2、(2015·浙江)计算:_______, _______.
解析
;
.
指数或对数与方程的结合多以选择题、填空题的形式出现,考查对数的运算性质及指数幂的运算性质及其方程的解法,难度偏低,分值一般为5分,属于基础题.
高考真题再现
考点2 由对数与指数幂的运算性质求未知数
典例剖析
例3、(2015·上海)方程的解为__________.
解析
高考真题再现
,
,
,即,
,
或,
解得或.
经检验,不满足条件,舍去.
.
对数的求值与化简在高考中出现的概率不大,往往借助对数运算性质与换底公式来解决问题,主要以选择题、填空题的形式出现,分值一般为5分,难度中等或偏上.
高考真题再现
考点3 对数的求值与化简
典例剖析
例4、(2016·浙江)已知,若,则______,______.
解析
高考真题再现
设,由知,
代入得,
即,解得或(舍去),
所以,即.
因为,所以,则,
解得.
典例剖析
例5、(2015·天津)已知,则当a的值为_______时, 取得最大值.
解析
高考真题再现
由已知条件得,令,
则
,
所以当,即时,取得最大值.
指数与对数的实际应用在高考中一般以选择题、填空题的形式出现,分值一般为5分,难度不大,属于基础题.
高考真题再现
考点4 指数、对数的实际应用
典例剖析
例6、(2014·湖南)某市生产总值连续两年持续增加,第一年的增长率为p,第二年的增长率为q,则该市这两年生产总值的年平均增长率为 ( )
A. B.
C. D.
解析
设该市这两年生产总值的年平均增长率为x,
则
解得.
D
高考真题再现
典例剖析
例7、(2019·北京)在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足,其中星等为的星的亮度为.已知太阳的星等是,天狼星的星等是,则太阳与天狼星的亮度的比值为 ( )
A. B. C. D.
解析
设太阳的星等是,天狼星的星等是,
由题意得 ,
即,则.
A
高考真题再现
苏教版同步教材精品课件
《指数与对数》章末复习
知识网络建构
指数幂运算的一般原则:
(1)有括号的先算括号里面的,无括号的先做指数运算.
(2)先乘除后加减,负指数幂化成正指数幂的倒数.
(3)底数是负数的,先确定符号;底数是小数的,先化成分数;底数是带分数的,先化成假分数.
(4)若是根式,应化为分数指数幂,尽可能用幂的形式表示,运用指数幂的运算性质来解答.
主要考查角度:
(1)根式与分数指数幂的互化;
(2)指数幂的化简;
(3)根式的性质与应用;
(4)分数指数幂的运算.
知识要点整合
一、指数的概念及运算
知识要点整合
典例剖析
解析
原式.
例1、_______(用分数指数幂表示)
例2、________.
解析
.
知识要点整合
典例剖析
分析
如果根式的被开方数不是的形式,先利用乘法公式将被开方数化成的形式,然后再利用的性质进行化简或运算.
例3、化简下列各式:
(1);(2);
(3).
解析
(1)
(2)原式
.
当,即时,
.
当,即时,
知识要点整合
典例剖析
如果根式的被开方数不是的形式,先利用乘法公式将被开方数化成的形式,然后再利用的性质进行化简或运算.
例3、化简下列各式:
(1);(2);
(3).
解析
(3)原式.
当时,原式;
当时,原式.
分析
知识要点整合
典例剖析
分析
依据下列法则运算:①先进行指数运算,在进行指数运算时可将底数化成幂的形式,再利用幂的乘方进行运算;②对于零次幂,直接运用得出结论;③底数为带分数的化成假分数,进而将底数化成幂的形式;④底数为小数的一般化成分数来运算;⑤先算乘方(开方),再算乘除,最后算加减.
例4、化简下列各式:
(1);
(2);
(3).
知识要点整合
典例剖析
例4、化简下列各式:
(1);
(2);
(3).
解析
(1)原式.
(2)原式.
(3)原式
.
条件求值问题是代数式求值问题中的常见题型,一般要结合已知条件先化简再求值.另外,要特别注意条件的应用,如条件中的隐含条件、整体代入等,可以简化解题过程.
解决此类问题的一般步骤:
(1)审题:从整体上把握已知条件和所求代数式的特点;
(2)化简:化简已知条件与所求代数式;
(3)求值:把条件代入求值.
主要考查角度:
(1)“已知值”的化简求值;
(2)利用“整体代入”化简求值.
知识要点整合
二、指数中条件因式的化简与求值
知识要点整合
典例剖析
分析
先对所求代数式进行化简,然后将x,y的值代入进行运算.
例5、已知,求的值.
解析
.
,
原式.
知识要点整合
典例剖析
例6、已知,则的值为 ( )
A.7 B. C. D.27
解析
由,两边平方得,则.
A
运算的一般思路:
(1)首先利用幂的运算把底数或真数进行变形,化成分数指数幂的形式,使幂的底数最简,然后正用对数运算性质化简合并.
(2)将对数式化为同底数对数的和、差、倍数运算,然后逆用对数的运算性质,转化为同底对数真数的积、商、幂的运算.
主要考查角度:
(1)对数式与指数式的互化;
(2)利用指数式与对数式的互化求变量x的值;
(3)对数的求值与化简;
(4)对数方程问题.
知识要点整合
三、对数的概念及运算对数
知识要点整合
典例剖析
例7、下列指数式与对数式互化不正确的一组是 ( )
A.=1与 B. 与
C.与 D. 与
解析
A.=1与 ;正确;
B. 与,正确;
C.应该化为,不正确;
D. 与,正确.
C
知识要点整合
典例剖析
分析
先将对数式化为指数式,然后利用指数幂的运算性质求解.
例8、求下列各式中x的值;
(1);(2).
解析
由(1)得,故.
(2)由得 ,故.
例9、计算_______.
解析
原式.
知识要点整合
典例剖析
例10、设的两根分别是,则 ( )
A. B. C. D.
解析
的两根分别是,
和是方程两个根,
则.
.
D
利用对数的换底公式以将不同底的对数问题化为同底的对数问题.解题时,首先要观察底数是否相同,若不同,则应用换底公式进行转化,然后运用对数的运算性质进行化简、计算换底时,要注意与题中条件结合,所取的底数要便于计算.
主要考查角度:
(1)利用换底公式求值;
(2)利用换底公式解决条件求值问题.
知识要点整合
四、对数换底公式的应用
知识要点整合
典例剖析
例11、设的值为 ( )
A. 18 B. C. D.
解析
原式.
C
例12、已知,则_________(用表示).
解析
.
数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养.主要包括:理解运算对象,掌握运算法则,探究运算思路,选择运算方法,设计运算程序,求得运算结果等.
本章内容中,利用指数幂的运算性质进行化简或计算,利用对数的运算性质进行化简或计算等方面涉及数学运算核心素养.
核心素养梳理
一、数学运算
典例剖析
例1、化简:.
解析
原式
.
分析
利用指数幂的运算性质进行化简.
核心素养梳理
典例剖析
例2、求值:(1);(2);
(3).
解析
(1)原式.
(2)原式.
(3)原式.
分析
利用对数的运算性质进行计算.
核心素养梳理
逻辑推理是指从一些事实和命题出发,依据规则推出其他命题的素养.逻辑推理主要表现为:掌握推理基本形式和规则,发现问题和提出命题,探索和表述论证过程,理解命题体系,有逻辑地表达与交流.
本章内容中,类比正整数指数幂理解有理数指数幂、无理数指数幂的概念,类比指数幂的运算性质学习对数的运算性质等方面涉及逻辑推理核心素养.
核心素养梳理
二、逻辑推理
典例剖析
例3、已知,求下列各式的值:
(1); (2); (3);(4).
解析
(1)由两边平方,得,即.
(2)由 ,得,即.
.
.
分析
从整体上寻找待求各式与条件的联系,进而整体代入求值.
核心素养梳理
典例剖析
例3、已知,求下列各式的值:
(1); (2); (3);(4).
解析
(3),
.
(4), ,即.
原式.
分析
从整体上寻找待求各式与条件的联系,进而整体代入求值.
核心素养梳理
指数与对数的运算在高考中很少单独命题,它往往作为解决指数函数与对数函数的工具,若单独命题多以填空题的形式出现,分值一般为5分,属于基础题.
高考真题再现
考点1 指数与对数运算
典例剖析
例1、(2015·安徽)______.
解析
.
高考真题再现
例2、(2015·浙江)计算:_______, _______.
解析
;
.
指数或对数与方程的结合多以选择题、填空题的形式出现,考查对数的运算性质及指数幂的运算性质及其方程的解法,难度偏低,分值一般为5分,属于基础题.
高考真题再现
考点2 由对数与指数幂的运算性质求未知数
典例剖析
例3、(2015·上海)方程的解为__________.
解析
高考真题再现
,
,
,即,
,
或,
解得或.
经检验,不满足条件,舍去.
.
对数的求值与化简在高考中出现的概率不大,往往借助对数运算性质与换底公式来解决问题,主要以选择题、填空题的形式出现,分值一般为5分,难度中等或偏上.
高考真题再现
考点3 对数的求值与化简
典例剖析
例4、(2016·浙江)已知,若,则______,______.
解析
高考真题再现
设,由知,
代入得,
即,解得或(舍去),
所以,即.
因为,所以,则,
解得.
典例剖析
例5、(2015·天津)已知,则当a的值为_______时, 取得最大值.
解析
高考真题再现
由已知条件得,令,
则
,
所以当,即时,取得最大值.
指数与对数的实际应用在高考中一般以选择题、填空题的形式出现,分值一般为5分,难度不大,属于基础题.
高考真题再现
考点4 指数、对数的实际应用
典例剖析
例6、(2014·湖南)某市生产总值连续两年持续增加,第一年的增长率为p,第二年的增长率为q,则该市这两年生产总值的年平均增长率为 ( )
A. B.
C. D.
解析
设该市这两年生产总值的年平均增长率为x,
则
解得.
D
高考真题再现
典例剖析
例7、(2019·北京)在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足,其中星等为的星的亮度为.已知太阳的星等是,天狼星的星等是,则太阳与天狼星的亮度的比值为 ( )
A. B. C. D.
解析
设太阳的星等是,天狼星的星等是,
由题意得 ,
即,则.
A
高考真题再现
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
