苏教版(2019)高中数学必修第一册 《函数的图象》精品课件(共17张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学必修第一册 《函数的图象》精品课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-11 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
苏教版同步教材精品课件
5.1.2函数的图象
情境引入
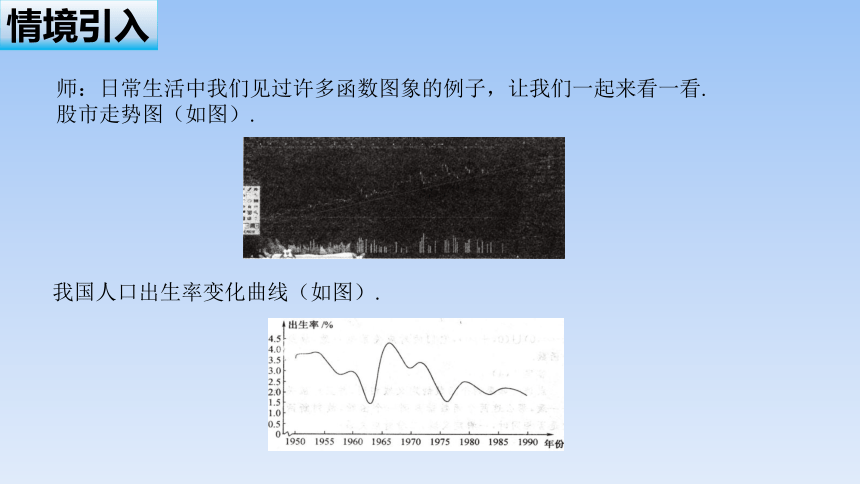
师:日常生活中我们见过许多函数图象的例子,让我们一起来看一看.
股市走势图(如图).
我国人口出生率变化曲线(如图).
情境引入
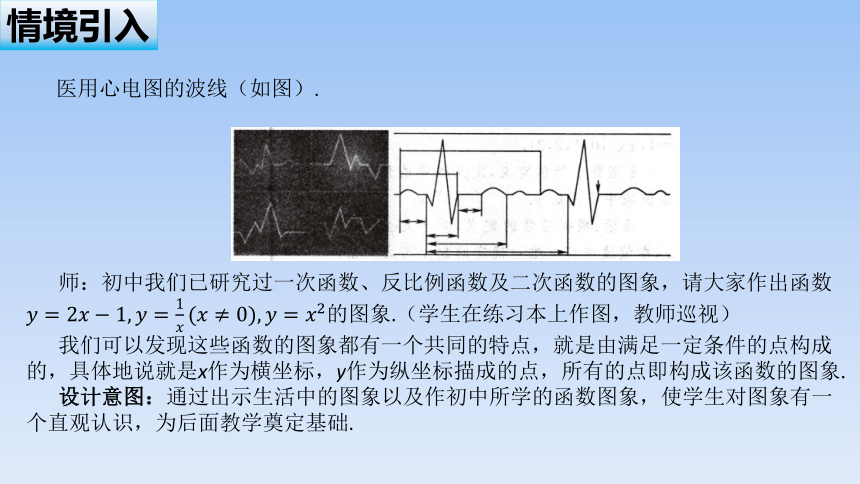
医用心电图的波线(如图).
师:初中我们已研究过一次函数、反比例函数及二次函数的图象,请大家作出函数的图象.(学生在练习本上作图,教师巡视)
我们可以发现这些函数的图象都有一个共同的特点,就是由满足一定条件的点构成的,具体地说就是x作为横坐标,y作为纵坐标描成的点,所有的点即构成该函数的图象.
设计意图:通过出示生活中的图象以及作初中所学的函数图象,使学生对图象有一个直观认识,为后面教学奠定基础.
1.函数的图象
思考:一般而言,如何作出函数的图象呢?
函数的图象的定义:将自变量的一个值作为横坐标,相应的函数值作为纵坐标,就得到坐标平面上的一个点.当自变量取遍函数定义域A中的每一个值时,就得到一系列这样的点.所有这些点组成的.
集合(点集)为,即,所有这些点组成的图形就是函数的图象.
可从以下几个方面加深对函数图象的理解:
画函数的图象,不仅要依据函数的解析式,而且还必须考虑它的定义域.两个用不同的解析式表示的函数,只有在对应关系相同、定义域相同的条件下,才能是同一个函数,才能有相同的图象.
讲解新课
由函数的图象的定义可知,点的集合是函数的图象,因此从理论上讲,用列表描点法总能作出函数的图象,但是不了解函数本身的特点,就无法了解函数图象的特点,如二次函数的图象是抛物线,如果不知道抛物线的顶点坐标和对称轴,盲目地列表描点是很难将图象的特征描绘出来的.
函数的图象是函数的重要表示方法,它具有明显的直观性,通过函数的图象能够掌握函数的重要性质.反之,掌握好函数的性质,将有助于正确地作出函数的图象.
设计意图:用严谨的数学语言给出函数的图象的定义,使学生的认知得到提升,发展学生的数学抽象核心素养.
讲解新课
讲解新课
2.典例分析.
我们知道函数的图象是由点集中的点组成的图形,如何作图即如何选点呢?我们看一看下面的一些例题.
典例剖析
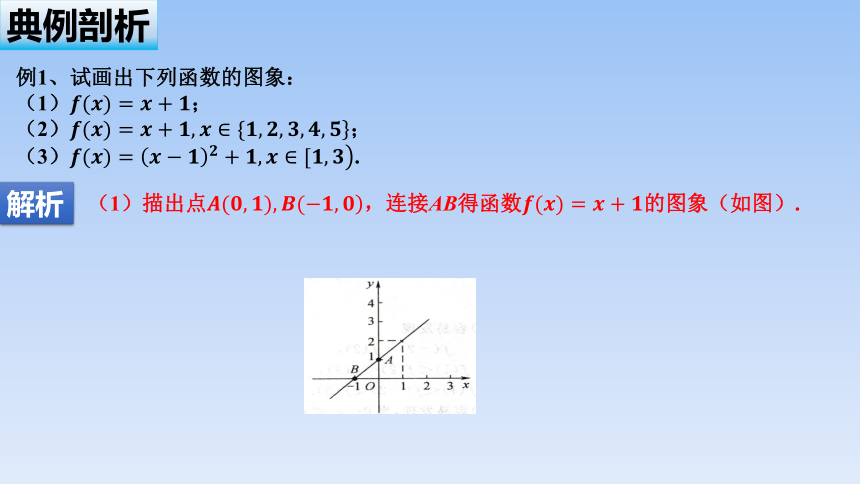
例1、试画出下列函数的图象:
(1);
(2);
(3).
解析
(1)描出点,连接AB得函数的图象(如图).
典例剖析
例1、试画出下列函数的图象:
(1);
(2);
(3).
解析
(2)先列表,再描点.
师:如图(1)就是作出的函数图象,它是由一些散点组成的.换句话说,就是函数的图象可以是一些散点.如何由它得到函数的图象呢?
生:仅需把图(1)的散点连接起来构成一条直线,这条直线就是函数的图象,如图(2).
师:对,在初中我们就研究过一次函数的图象,它是一条直线,所以今后我们作一次函数的图象仅需描出其中两点,然后连成一条直线即可.
典例剖析
例1、试画出下列函数的图象:
(1);
(2);
(3).
解析
(3)师:这是什么曲线?
生:抛物线.
师:是一条完整的抛物线吗?
生:好像不是.
师:为什么?
生:因为,所以x的取值受限制.
师:对,这个函数的图象与函数的图象有联系,它是其中一段.为了能够作出其图象,我们先作出函数的图象,大家自己动手作出此图象,用虚线表示.(一会儿后)请甲同学回答如何作出此图象.
典例剖析
例1、试画出下列函数的图象:
(1);
(2);
(3).
解析
生甲:先作出顶点,再作出两点,然后根据抛物线的对称轴是直线,作出关于直线的对称点然后顺次用光滑的曲线连接这五个点,从而得到函数的图象,如图(3).
师:甲同学先选关键点即顶点,再结合二次函数图象的对称性取另外两点作出其关于对称轴的对称点,这样得到5个点,最后用光滑的曲线由左向右顺次连接这些点.这种方法是通常作二次函数的图象的方法.
这种方法提醒我们,对一些熟知的函数,要作出其图象仅需要选一些特征点及辅助点,然后连接这些点就可以得出其图象.
典例剖析
这样要作出函数的图象,仅需要在函数的图象上取的一段用实线描出,其中,点图象上,用实心点表示;而点在图象上,用空心点表示,如图(4).
设计意图:由简单的连续的图象到离散型图象、图象的一部分,使学生对于函数图象的认识更加全面.
典例剖析
例2、在教材5.1节开头的第一个问题中,如果把人口数y(百万)看作年份x的函数,试根据教材表5—1—1,画出这个函数的图象.
解析
由教材表5—1—1的数据,画出的函数图象是8个点,如图所示.
设计意图:使学生认识到数学知识在实际生活中应用广泛.
典例剖析
思考:设函数的定义域为A,集合相等吗?请说明理由.
教师根据函数的图象的概念引导学生分析后得出:
集合P表示函数图象上所有点的集合,而集合Q表示函数图象上所有点的纵坐标的集合,也就是函数的值域,二者一个是点集,一个是数集,完全不同.
典例剖析
例3、试画出二次函数的图象,并根据图象回答下列问题:
(1)比较的大小;
(2)若,试比较与的大小.
解析
函数图象如图(1)(2).
(1)根据图(1)容易发现,,所以.
(2)根据图(2)容易发现,当时,.
典例剖析
说明:由说明点与关于y轴对称.
思考:在例3(2)中,
(1)如果把“”改为“”,那么与的大小如何?
(2)如果把“”改为“ ”,那么与大小如何?
教师引导学生根据图象得到:
(1);(2).
设计意图:让学生体会函数图象的应用性,为后面学习函数的单调性、奇偶性奠定基础.
3.信息技术下的函数图象.
让学生阅读教材第103~104页关于信息技术的内容,有条件的可以让学生尝试利用电脑绘图..
课堂小结
1.本节学习的数学知识:
函数的图象、函数图象的作法、函数图象的应用.
2.本节学习的数学方法:
数形结合与分类讨论的思想方法.
作 业
教材第104页练习第1,2,3题.
苏教版同步教材精品课件
5.1.2函数的图象
情境引入
师:日常生活中我们见过许多函数图象的例子,让我们一起来看一看.
股市走势图(如图).
我国人口出生率变化曲线(如图).
情境引入
医用心电图的波线(如图).
师:初中我们已研究过一次函数、反比例函数及二次函数的图象,请大家作出函数的图象.(学生在练习本上作图,教师巡视)
我们可以发现这些函数的图象都有一个共同的特点,就是由满足一定条件的点构成的,具体地说就是x作为横坐标,y作为纵坐标描成的点,所有的点即构成该函数的图象.
设计意图:通过出示生活中的图象以及作初中所学的函数图象,使学生对图象有一个直观认识,为后面教学奠定基础.
1.函数的图象
思考:一般而言,如何作出函数的图象呢?
函数的图象的定义:将自变量的一个值作为横坐标,相应的函数值作为纵坐标,就得到坐标平面上的一个点.当自变量取遍函数定义域A中的每一个值时,就得到一系列这样的点.所有这些点组成的.
集合(点集)为,即,所有这些点组成的图形就是函数的图象.
可从以下几个方面加深对函数图象的理解:
画函数的图象,不仅要依据函数的解析式,而且还必须考虑它的定义域.两个用不同的解析式表示的函数,只有在对应关系相同、定义域相同的条件下,才能是同一个函数,才能有相同的图象.
讲解新课
由函数的图象的定义可知,点的集合是函数的图象,因此从理论上讲,用列表描点法总能作出函数的图象,但是不了解函数本身的特点,就无法了解函数图象的特点,如二次函数的图象是抛物线,如果不知道抛物线的顶点坐标和对称轴,盲目地列表描点是很难将图象的特征描绘出来的.
函数的图象是函数的重要表示方法,它具有明显的直观性,通过函数的图象能够掌握函数的重要性质.反之,掌握好函数的性质,将有助于正确地作出函数的图象.
设计意图:用严谨的数学语言给出函数的图象的定义,使学生的认知得到提升,发展学生的数学抽象核心素养.
讲解新课
讲解新课
2.典例分析.
我们知道函数的图象是由点集中的点组成的图形,如何作图即如何选点呢?我们看一看下面的一些例题.
典例剖析
例1、试画出下列函数的图象:
(1);
(2);
(3).
解析
(1)描出点,连接AB得函数的图象(如图).
典例剖析
例1、试画出下列函数的图象:
(1);
(2);
(3).
解析
(2)先列表,再描点.
师:如图(1)就是作出的函数图象,它是由一些散点组成的.换句话说,就是函数的图象可以是一些散点.如何由它得到函数的图象呢?
生:仅需把图(1)的散点连接起来构成一条直线,这条直线就是函数的图象,如图(2).
师:对,在初中我们就研究过一次函数的图象,它是一条直线,所以今后我们作一次函数的图象仅需描出其中两点,然后连成一条直线即可.
典例剖析
例1、试画出下列函数的图象:
(1);
(2);
(3).
解析
(3)师:这是什么曲线?
生:抛物线.
师:是一条完整的抛物线吗?
生:好像不是.
师:为什么?
生:因为,所以x的取值受限制.
师:对,这个函数的图象与函数的图象有联系,它是其中一段.为了能够作出其图象,我们先作出函数的图象,大家自己动手作出此图象,用虚线表示.(一会儿后)请甲同学回答如何作出此图象.
典例剖析
例1、试画出下列函数的图象:
(1);
(2);
(3).
解析
生甲:先作出顶点,再作出两点,然后根据抛物线的对称轴是直线,作出关于直线的对称点然后顺次用光滑的曲线连接这五个点,从而得到函数的图象,如图(3).
师:甲同学先选关键点即顶点,再结合二次函数图象的对称性取另外两点作出其关于对称轴的对称点,这样得到5个点,最后用光滑的曲线由左向右顺次连接这些点.这种方法是通常作二次函数的图象的方法.
这种方法提醒我们,对一些熟知的函数,要作出其图象仅需要选一些特征点及辅助点,然后连接这些点就可以得出其图象.
典例剖析
这样要作出函数的图象,仅需要在函数的图象上取的一段用实线描出,其中,点图象上,用实心点表示;而点在图象上,用空心点表示,如图(4).
设计意图:由简单的连续的图象到离散型图象、图象的一部分,使学生对于函数图象的认识更加全面.
典例剖析
例2、在教材5.1节开头的第一个问题中,如果把人口数y(百万)看作年份x的函数,试根据教材表5—1—1,画出这个函数的图象.
解析
由教材表5—1—1的数据,画出的函数图象是8个点,如图所示.
设计意图:使学生认识到数学知识在实际生活中应用广泛.
典例剖析
思考:设函数的定义域为A,集合相等吗?请说明理由.
教师根据函数的图象的概念引导学生分析后得出:
集合P表示函数图象上所有点的集合,而集合Q表示函数图象上所有点的纵坐标的集合,也就是函数的值域,二者一个是点集,一个是数集,完全不同.
典例剖析
例3、试画出二次函数的图象,并根据图象回答下列问题:
(1)比较的大小;
(2)若,试比较与的大小.
解析
函数图象如图(1)(2).
(1)根据图(1)容易发现,,所以.
(2)根据图(2)容易发现,当时,.
典例剖析
说明:由说明点与关于y轴对称.
思考:在例3(2)中,
(1)如果把“”改为“”,那么与的大小如何?
(2)如果把“”改为“ ”,那么与大小如何?
教师引导学生根据图象得到:
(1);(2).
设计意图:让学生体会函数图象的应用性,为后面学习函数的单调性、奇偶性奠定基础.
3.信息技术下的函数图象.
让学生阅读教材第103~104页关于信息技术的内容,有条件的可以让学生尝试利用电脑绘图..
课堂小结
1.本节学习的数学知识:
函数的图象、函数图象的作法、函数图象的应用.
2.本节学习的数学方法:
数形结合与分类讨论的思想方法.
作 业
教材第104页练习第1,2,3题.
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
